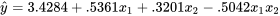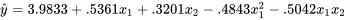8.1.5 Interactions
Précédemment dans cette section, il a été question du fait qu’un « terme en  » dans les équations d’ajustement par les moindres carrés peut être une fonction connue (par exemple, un logarithme) d’une variable de base du processus. En fait, il est souvent utile de permettre à un « terme
» dans les équations d’ajustement par les moindres carrés peut être une fonction connue (par exemple, un logarithme) d’une variable de base du processus. En fait, il est souvent utile de permettre à un « terme  » d’être fonction de plusieurs variables de base du processus, comme on le voit dans l’exemple suivant.
» d’être fonction de plusieurs variables de base du processus, comme on le voit dans l’exemple suivant.
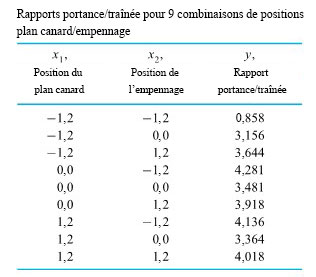
Exemple 8.1.5.1 : Rapport portance/traînée pour une configuration à trois surfaces
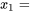 le placement du plan canard en pouces au-dessus du plan de l’aile principale
le placement du plan canard en pouces au-dessus du plan de l’aile principale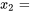 l’emplacement de l’empennage en pouces au-dessus du plan de l’aile principale
l’emplacement de l’empennage en pouces au-dessus du plan de l’aile principale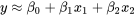
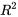 de seulement 0,394. Même l’ajout de termes au carré à
de seulement 0,394. Même l’ajout de termes au carré à  et
et 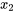 , c’est-à-dire l’ajustement de l’équation
, c’est-à-dire l’ajustement de l’équation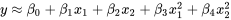
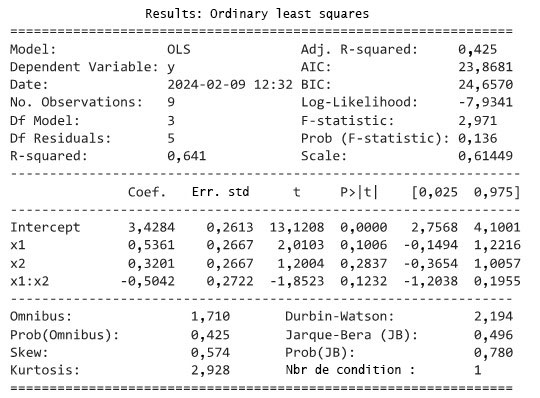
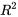 à seulement 0,513. Cependant, la capture d’écran 8.1.5.1 montre que l’ajustement de l’équation
à seulement 0,513. Cependant, la capture d’écran 8.1.5.1 montre que l’ajustement de l’équation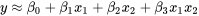
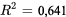 , pour la fonction suivante :
, pour la fonction suivante :8.1.5.1
.
.

.
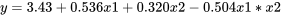
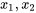 , et
, et  du tableau 8.1.5.1 dans les colonnes, les produits
du tableau 8.1.5.1 dans les colonnes, les produits 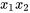 ont été créés et
ont été créés et  ajustés aux trois variables prédictives
ajustés aux trois variables prédictives 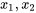 , et
, et 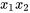 afin de créer cette capture d’écran.)
afin de créer cette capture d’écran.) ) semble avoir des effets visiblement différents sur
) semble avoir des effets visiblement différents sur  en fonction de la valeur de
en fonction de la valeur de 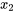 (la position de l’empennage). (Il semble que le canard et l’empennage ne doivent pas être alignés, c’est-à-dire que
(la position de l’empennage). (Il semble que le canard et l’empennage ne doivent pas être alignés, c’est-à-dire que  ne doit pas être proche de
ne doit pas être proche de 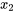 . Pour maximiser la fonction,
. Pour maximiser la fonction,  doit être petit si
doit être petit si 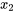 est grand, et vice-versa.) C’est le terme mixte
est grand, et vice-versa.) C’est le terme mixte 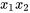 dans l’équation 8.1.5.1 qui permet aux courbes de réponse d’avoir des caractères différents pour différentes valeurs de
dans l’équation 8.1.5.1 qui permet aux courbes de réponse d’avoir des caractères différents pour différentes valeurs de 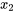 . Sans ce terme, les tranches de la surface ajustée
. Sans ce terme, les tranches de la surface ajustée 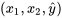 seraient parallèles pour différentes valeurs de
seraient parallèles pour différentes valeurs de 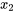 , comme dans la situation du module 8.1.4.
, comme dans la situation du module 8.1.4.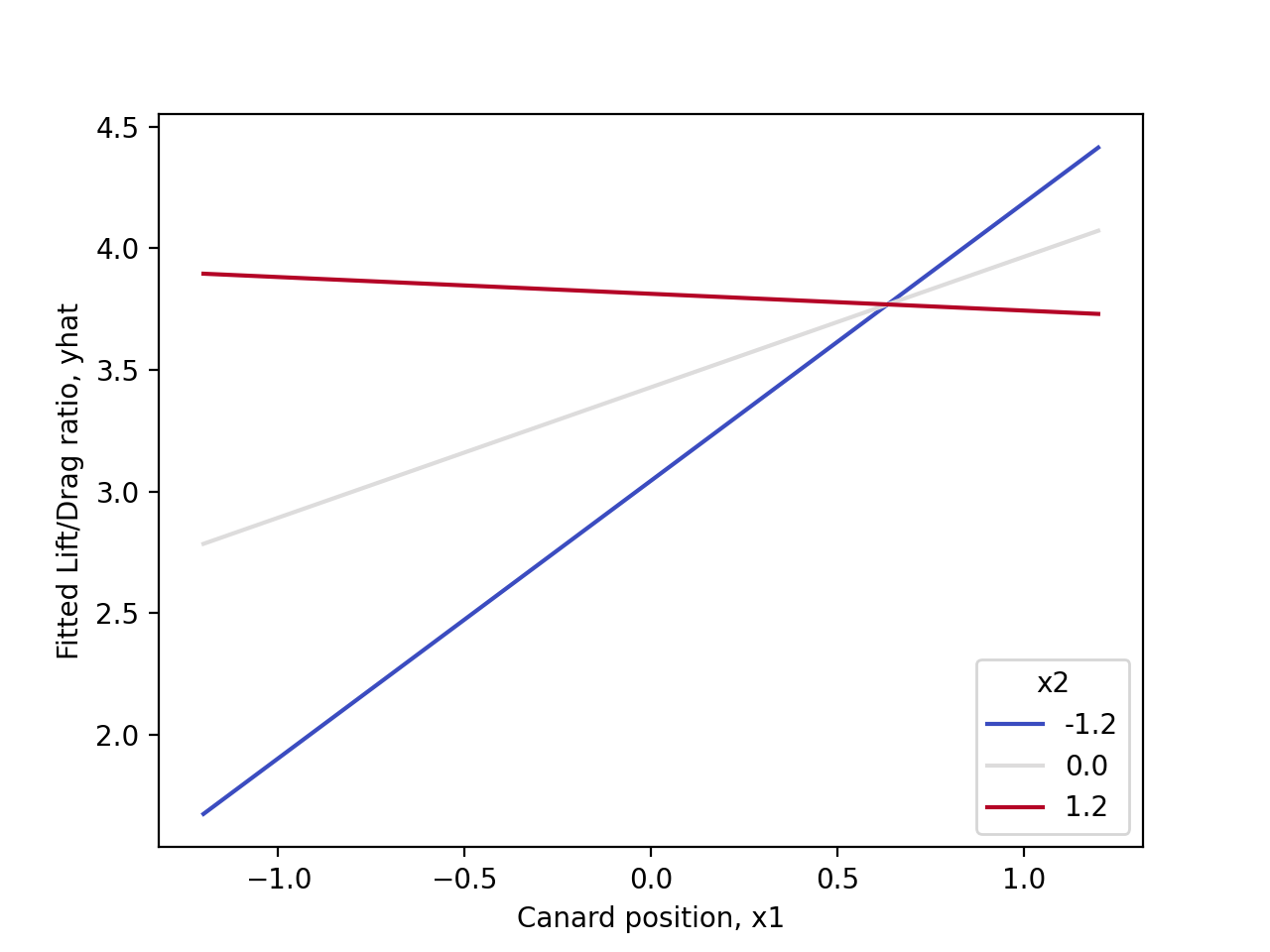
.
 ; on peut observer une forte tendance curvilinéaire. En fait, pour l’équation ajustée
; on peut observer une forte tendance curvilinéaire. En fait, pour l’équation ajustée8.1.5.2
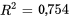 et des résidus qui semblent généralement aléatoires. En traçant les courbes
et des résidus qui semblent généralement aléatoires. En traçant les courbes 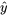 en fonction de
en fonction de  pour plusieurs valeurs de
pour plusieurs valeurs de 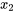 , on peut voir que l’équation ajustée 8.1.5.2 produit des tranches paraboliques non parallèles de la surface ajustée
, on peut voir que l’équation ajustée 8.1.5.2 produit des tranches paraboliques non parallèles de la surface ajustée 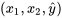 , au lieu des tranches linéaires non parallèles observées sur la figure 8.1.5.1.
, au lieu des tranches linéaires non parallèles observées sur la figure 8.1.5.1.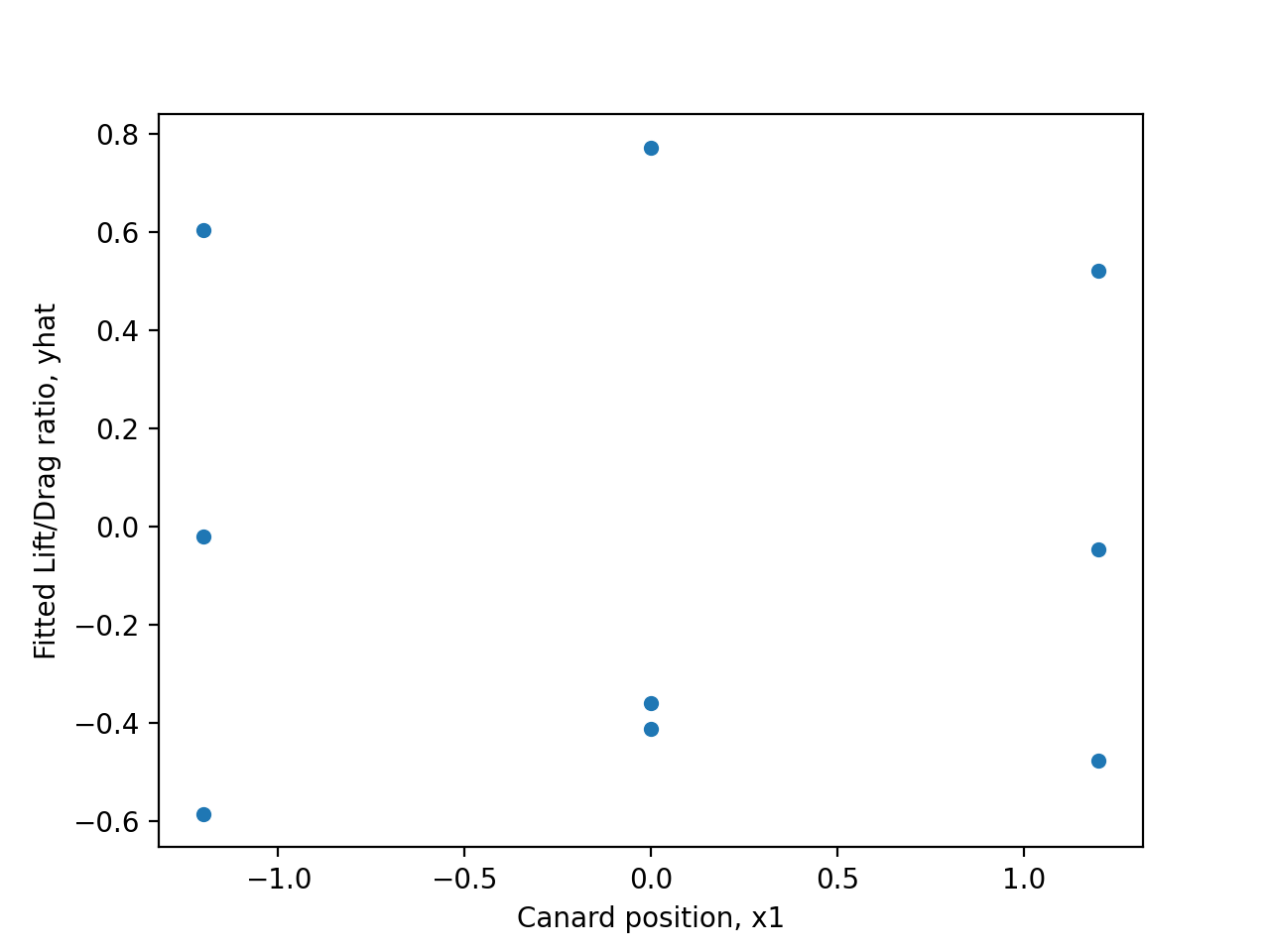
.
Cet exemple est disponible dans le Python Jupyter Notebook sur le site GitHub du cours.
Vous pouvez également utiliser le lien Binder suivant pour réviser cet exemple dans un environnement interactif (site GitHub spécial pour l’exemple 8.1.5) : consulter l’exemple 8.1.5 sur Binder.