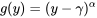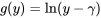8.1.2 Transformations
Transformations pour la régression linéaire
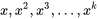 de l’équation 8.1.12 peuvent être remplacés par n’importe quelle fonction (connue) de
de l’équation 8.1.12 peuvent être remplacés par n’importe quelle fonction (connue) de  sans changer le reste de l’analyse. Les équations normales consisteront toujours en
sans changer le reste de l’analyse. Les équations normales consisteront toujours en 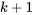 équations linéaires de paramètres
équations linéaires de paramètres 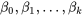 , et un programme de régressions linéaire multiple produira toujours les valeurs de moindres carrés
, et un programme de régressions linéaire multiple produira toujours les valeurs de moindres carrés 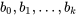 . Cela peut toujours être très utile quand il existe des raisons théoriques de supposer que
. Cela peut toujours être très utile quand il existe des raisons théoriques de supposer que  et
et  sont liées par une fonction simple mais non linéaire. Par exemple, l’équation de Taylor pour la durée de vie des outils est de la forme
sont liées par une fonction simple mais non linéaire. Par exemple, l’équation de Taylor pour la durée de vie des outils est de la forme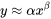
 est la durée de vie de l’outil (par exemple, en minutes) et
est la durée de vie de l’outil (par exemple, en minutes) et  la vitesse de coupe appliquée (par exemple, en m/min). En prenant le logarithme des deux côtés de l’équation, on obtient :
la vitesse de coupe appliquée (par exemple, en m/min). En prenant le logarithme des deux côtés de l’équation, on obtient :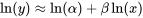
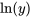 et la variable
et la variable 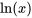 , et dont les paramètres
, et dont les paramètres 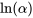 et
et 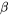 sont linéaires. Ainsi, à partir d’un ensemble de données
sont linéaires. Ainsi, à partir d’un ensemble de données 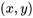 , on détermine les valeurs empiriques de
, on détermine les valeurs empiriques de 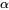 et
et 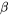 en faisant ce qui suit :
en faisant ce qui suit : et des
et des  .
.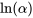 comme valeur
comme valeur 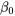 (et ainsi
(et ainsi 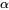 avec
avec 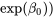 et
et 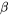 comme valeur
comme valeur 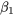 .
.Transformations de variables en modélisation
Transformations et échantillons uniques
Comme discuté dans les parties 3 et 4, il existe plusieurs distributions théoriques standard. Lorsqu’une de ces distributions peut être utilisée pour décrire une réponse  , tout ce qu’on sait à propos de ce modèle peut servir à faire des prédictions et inférences concernant
, tout ce qu’on sait à propos de ce modèle peut servir à faire des prédictions et inférences concernant  . Toutefois, lorsqu’aucune forme de distribution standard ne semble décrire
. Toutefois, lorsqu’aucune forme de distribution standard ne semble décrire  , il est néanmoins possible de définir une fonction
, il est néanmoins possible de définir une fonction 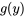 qui, elle, correspond à une distribution standard.
qui, elle, correspond à une distribution standard.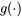
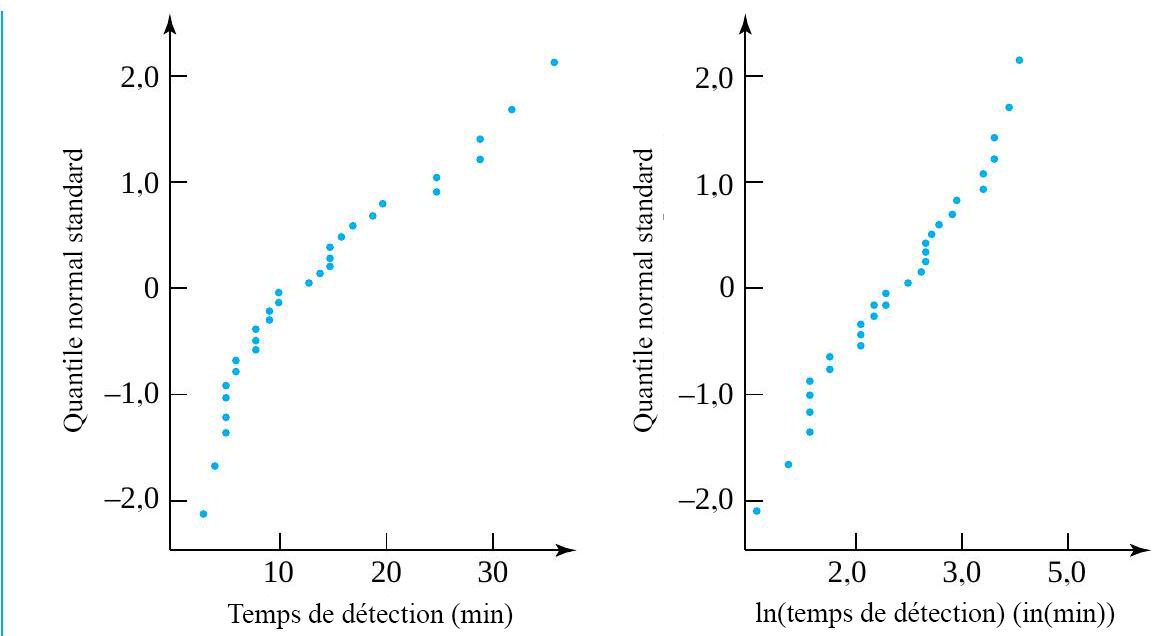
Exemple 8.1.2.1 Temps de détection
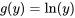 . Pour illustrer son utilisation dans le cas présent, des graphiques normaux des temps de détection et du logarithme des temps de détections sont présentés à la figure 8.1.2.2. Ces graphiques montrent qu’Elliot, Kibby et Meyer n’auraient pas pu raisonnablement appliquer les méthodes d’inférence standard aux temps de détection, mais qu’ils auraient pu les utiliser avec les logarithmes des temps de détection. Le second graphique normal est beaucoup plus linéaire que le premier.
. Pour illustrer son utilisation dans le cas présent, des graphiques normaux des temps de détection et du logarithme des temps de détections sont présentés à la figure 8.1.2.2. Ces graphiques montrent qu’Elliot, Kibby et Meyer n’auraient pas pu raisonnablement appliquer les méthodes d’inférence standard aux temps de détection, mais qu’ils auraient pu les utiliser avec les logarithmes des temps de détection. Le second graphique normal est beaucoup plus linéaire que le premier.
.
.
8.1.2.1 Transformations de puissance
 constitue généralement une valeur seuil, qui correspond à une valeur minimum de la réponse.
constitue généralement une valeur seuil, qui correspond à une valeur minimum de la réponse.  détermine la forme de base du graphique qui représente
détermine la forme de base du graphique qui représente  en fonction de
en fonction de  . Si
. Si 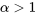 1″ title= »\alpha>1″ class= »latex mathjax »>, la transformation 8.1.2.1 a tendance à allonger la queue droite de la distribution de
1″ title= »\alpha>1″ class= »latex mathjax »>, la transformation 8.1.2.1 a tendance à allonger la queue droite de la distribution de  . Si <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/bbfc5cb85d863c86329fad1cca04a7de.png » alt= »0<\alpha<1″ title= »0<\alpha, la transformation a tendance à réduire la queue droite de la distribution de
. Si <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/bbfc5cb85d863c86329fad1cca04a7de.png » alt= »0<\alpha<1″ title= »0<\alpha, la transformation a tendance à réduire la queue droite de la distribution de  ; la réduction devient plus prononcée à mesure que
; la réduction devient plus prononcée à mesure que 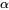 s’approche de 0, mais elle n’est jamais aussi prononcée que lorsqu’on utilise une transformation logarithmique
s’approche de 0, mais elle n’est jamais aussi prononcée que lorsqu’on utilise une transformation logarithmique8.1.2.2 Transformation logarithmique
.
Transformations et échantillons multiples
Comparer plusieurs ensembles de conditions d’un processus constitue l’un des problèmes fondamentaux de l’analyse statistique en ingénierie. Il est préférable d’effectuer la comparaison en utilisant une échelle où les échantillons présentent des variabilités comparables, pour au moins deux raisons. Premièrement, les comparaisons sont alors simplement réduites à la comparaison entre les moyennes des réponses. Deuxièmement, les propriétés des méthodes standard d’inférence statistique ne sont souvent bien comprises que lorsque la variabilité des réponses est comparable pour les différents ensembles de conditions.
.
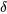 de la moyenne de la réponse, essayer la transformation 8.1.2.1 avec
de la moyenne de la réponse, essayer la transformation 8.1.2.1 avec 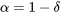 .
.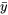 et
et 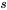 ), une manière empirique de déterminer si les consignes 1) ou 2) ci-dessus peuvent être utiles consiste à tracer
), une manière empirique de déterminer si les consignes 1) ou 2) ci-dessus peuvent être utiles consiste à tracer 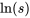 en fonction de
en fonction de 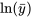 , puis à voir s’il existe une linéarité approximative. Si tel est le cas, la consigne 1) est appropriée quand la pente est approximativement égale à 1, tandis qu’une pente de
, puis à voir s’il existe une linéarité approximative. Si tel est le cas, la consigne 1) est appropriée quand la pente est approximativement égale à 1, tandis qu’une pente de 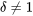 indique qu’il faut utiliser la consigne 2) et suggère la valeur à utiliser.
indique qu’il faut utiliser la consigne 2) et suggère la valeur à utiliser.