7.2.6 Calculs statistiques pour la régression linéaire simple : exemple de la pression et de la densité

Les logiciels statistiques simplifient un grand nombre des calculs nécessaires à l’application des méthodes décrites dans cette section. Aucune des méthodes de cette section n’est complexe au point de nécessiter absolument l’utilisation d’un tel logiciel, mais il est utile d’envisager d’en utiliser un dans le contexte de la régression linéaire simple. Apprendre où trouver, sur une capture d’écran typique, les diverses données sommaires correspondant
aux calculs effectués dans cette section permet de repérer d’importantes statistiques de synthèse pour les analyses compliquées de courbes et de surfaces présentées dans le prochain chapitre.

La capture d’écran 7.2.6.1 provient d’une analyse en Python dans JupyterLab Notebook des données de l’exemple portant sur la pression et la densité.  Le Notebook se trouve sur notre site GitHub à l’adresse suivante :  Intro Statistal Methods for Engineering GitHub Site, sous Part 7A.

Il est également possible de le consulter et de le télécharger sur le site GitHub spécial pour le chapitre 7.

Vous pouvez également ouvrir un environnement informatique interactif pour travailler avec le Jupyter Notebook utilisant Python à travers un site Binder en passant par le site GitHub de l’exemple de la partie 2.  Cliquez ici pour aller sur le site Binder (qui se trouve à l’adresse https://mybinder.org/v2/gh/Statistical-Methods-for-Engineering/Special-GitHub-Site-Part-2-Example-Percent-Waste-by-Weight-on-Bulk-Paper-Rolls/HEAD).

.

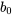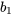La capture d’écran montre un exemple typique des résumés d’analyses de régression produites par les logiciels statistiques. Le renseignement le plus élémentaire est, bien entendu, l’équation de régression. Vient ensuite un sommaire d’un tableau donnant les coefficients estimés ( et ), leurs écarts-types estimés et les rapports t (pour tester si les coefficients β sont égaux à 0). La capture d’écran donne les valeurs d’échelle = 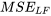= 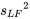et 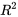.  Nous montrons également la capture d’écran d’un tableau d’ANOVA. Les niveaux de signification observés sont indiqués pour différentes statistiques de test. Le tableau d’ANOVA est suivi d’un tableau des valeurs de y, de y ajusté, de l’écart-type de y ajusté, des résidus et des résidus normalisés correspondant aux n points de données. Le programme de régression de Statsmodels en Python dispose d’une option qui permet de demander des valeurs ajustées, des intervalles de confidence pour 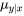et des intervalles de prévision pour x valeurs d’intérêt.  L’aperçu des captures d’écran se termine par les renseignements qui suivent pour la valeur x = 5 000.

Nous vous recommandons de comparer les renseignements figurant sur la capture d’écran 7.2.6.1 avec les divers résultats obtenus dans les exemples du chapitre 7 et de vérifier que ces valeurs sont comparables.  Nous poursuivrons notre apprentissage des autres éléments au chapitre 8.

The regression equation is
density = 2.375 + 4.867e-05 *pressure

                  Results: Ordinary least squares
===================================================================
Model:              OLS              Adj. R-squared:     0.981     
Dependent Variable: density          AIC:                -73.0762  
Date:               2024-01-30 15:06 BIC:                -71.6601  
No. Observations:   15               Log-Likelihood:     38.538    
Df Model:           1                F-statistic:        717.1     
Df Residuals:       13               Prob (F-statistic): 9.31e-13  
R-squared:          0.982            Scale:              0.00039636
---------------------------------------------------------------------
              Coef.    Std.Err.      t       P>|t|    [0.025   0.975]
---------------------------------------------------------------------
Intercept     2.3750     0.0121   197.0079   0.0000   2.3490   2.4010
pressure      0.0000     0.0000    26.7780   0.0000   0.0000   0.0001
-------------------------------------------------------------------
Omnibus:                2.101        Durbin-Watson:           1.682
Prob(Omnibus):          0.350        Jarque-Bera (JB):        0.427
Skew:                   0.137        Prob(JB):                0.808
Kurtosis:               3.780        Condition No.:           15556
===================================================================

ANOVA table

df    sum_sq   mean_sq           F        PR(>F)
pressure   1.0  0.284213  0.284213  717.060422  9.306841e-13
Residual  13.0  0.005153  0.000396         NaN           NaN

    pressure  density       Fit  StDev Fit  Residual  St Resid
0       2000    2.486  2.472333   0.008903  0.013667  0.767491
1       2000    2.479  2.472333   0.008903  0.006667  0.374386
2       2000    2.472  2.472333   0.008903 -0.000333 -0.018719
3       4000    2.558  2.569667   0.006296 -0.011667 -0.617705
4       4000    2.570  2.569667   0.006296  0.000333  0.017649
5       4000    2.580  2.569667   0.006296  0.010333  0.547110
6       6000    2.646  2.667000   0.005140 -0.021000 -1.091834
7       6000    2.657  2.667000   0.005140 -0.010000 -0.519921
8       6000    2.653  2.667000   0.005140 -0.014000 -0.727889
9       8000    2.724  2.764333   0.006296 -0.040333 -2.135495
10      8000    2.774  2.764333   0.006296  0.009667  0.511813
11      8000    2.808  2.764333   0.006296  0.043667  2.311982
12     10000    2.861  2.861667   0.008903 -0.000667 -0.037439
13     10000    2.879  2.861667   0.008903  0.017333  0.973403
14     10000    2.858  2.861667   0.008903 -0.003667 -0.205912

Predicted new value