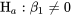7.2.5 Régression linéaire simple et ANOVA
La partie 6 a illustré comment, pour les études non structurées, la répartition de la somme totale des carrés en éléments interprétables fournit à la fois 1) une intuition et la quantification concernant l’origine de la variation observée et 2) la base d’un test F indiquant « aucune différence entre les moyennes ». Il s’avère que quelque chose de similaire est possible dans des contextes de régression linéaire simple.
Dans le contexte non structuré de la partie 6, il était utile de nommer la différence entre SCTot (somme totale des carrés) et SCE (somme des carrés d’erreur résiduelle). La convention correspondante pour l’ajustement des courbes et des surfaces est énoncée ci-dessous sous forme de définition.
DÉFINITION SOMME DES CARRÉS DE LA RÉGRESSION (SCR)
EXPRESSION 7.2.5.1
Dans les analyses de régression de courbes et de surface pour des études multi-échantillons, la différence
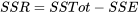
est appelée la somme des carrés de la régression (SCR).
La différence de la définition 7.2.5.1 a en général la forme d’une somme de carrés de quantités appropriées. Dans le cas présent (ajustement d’une droite par les moindres carrés), il s’agit de :
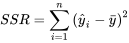
Sans utiliser la terminologie particulière de la définition 7.2.5.1 (ce manuel a déjà largement utilisé SCR = SCTot – SCE), un examen de la définition 7.1.2.2 (le coefficient de détermination 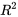 ) dans la partie 7.1 et des définitions de la partie 6 montrera que dans le contexte de courbes et de surfaces de régression :
) dans la partie 7.1 et des définitions de la partie 6 montrera que dans le contexte de courbes et de surfaces de régression :
7.2.5.1 Coefficient de détermination pour une régression linéaire simple dans la notation de la somme des carrés
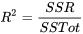
En d’autres termes, SCR est le numérateur du coefficient de détermination défini à la définition 7.1.2.2 (partie 7.1). Il est généralement considéré comme la partie de la variabilité brute de y qui est prise en compte dans le processus de régression de la courbe ou de la surface.
SCR et SCE ne fournissent pas seulement une répartition attrayante de SCTot, mais aussi les éléments pour effectuer un test F de
7.2.5.2
et de
7.2.5.3
Selon le modèle 7.2.1.2, l’hypothèse 7.2.5.2 peut être testée à l’aide de la statistique
7.2.5.4 Statistique de test F pour 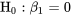
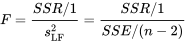
et d’une distribution 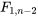 de référence, où des valeurs élevées observées de la statistique de test constituent une preuve contre
de référence, où des valeurs élevées observées de la statistique de test constituent une preuve contre 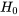 .
.
Précédemment dans cette section, l’hypothèse nulle générale 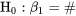 a été testée à l’aide de la variable t. Il est donc raisonnable d’examiner la relation entre le test F des équations 7.2.5.2, 7.2.5.3 et 7.2.5.4 et le test t précédent. L’hypothèse nulle
a été testée à l’aide de la variable t. Il est donc raisonnable d’examiner la relation entre le test F des équations 7.2.5.2, 7.2.5.3 et 7.2.5.4 et le test t précédent. L’hypothèse nulle 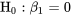 est un cas particulier de l’hypothèse
est un cas particulier de l’hypothèse 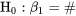 . C’est la version la plus fréquemment testée de l’hypothèse, puisqu’elle peut (dans certaines limites) être interprétée comme l’hypothèse nulle selon laquelle la réponse moyenne ne dépend pas de x. C’est parce que si l’hypothèse 7.2.5.2 est vraie dans le cadre du modèle de régression linéaire simple 7.2.1.2, on a
. C’est la version la plus fréquemment testée de l’hypothèse, puisqu’elle peut (dans certaines limites) être interprétée comme l’hypothèse nulle selon laquelle la réponse moyenne ne dépend pas de x. C’est parce que si l’hypothèse 7.2.5.2 est vraie dans le cadre du modèle de régression linéaire simple 7.2.1.2, on a 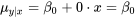 , qui ne dépend pas de x. (En fait, une meilleure interprétation d’un test de l’hypothèse 7.2.5.2 est qu’il s’agit de voir si un terme linéaire en x augmente de manière significative la capacité à modéliser la réponse y après avoir tenu compte d’une réponse moyenne globale.)
, qui ne dépend pas de x. (En fait, une meilleure interprétation d’un test de l’hypothèse 7.2.5.2 est qu’il s’agit de voir si un terme linéaire en x augmente de manière significative la capacité à modéliser la réponse y après avoir tenu compte d’une réponse moyenne globale.)
Si on examine ensuite les hypothèses 7.2.5.2 et 7.2.5.3, il peut sembler que la version # = 0 des équations du module 7 représente deux méthodes de test différentes. Or, elles sont équivalentes. La statistique 7.2.5.4 est le carré de la version # = 0 de la statistique, et les niveaux de signification (bilatéraux) observés basés sur la valeur et la distribution 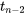 sont les mêmes que les niveaux de signification observés basés pour la statistique 7.2.5.2 et pour
sont les mêmes que les niveaux de signification observés basés pour la statistique 7.2.5.2 et pour 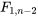 . Ainsi, le test F indiqué ici est redondant, compte tenu de la discussion précédente, mais il est présenté ici en raison de sa relation avec les idées d’ANOVA de la partie 6 et parce qu’il offre une généralisation naturelle importante dans des situations plus complexes d’ajustement de courbes et de surfaces. (Cette généralisation, qui sera abordée dans la partie 8, n’est pas équivalente à un test t.)
. Ainsi, le test F indiqué ici est redondant, compte tenu de la discussion précédente, mais il est présenté ici en raison de sa relation avec les idées d’ANOVA de la partie 6 et parce qu’il offre une généralisation naturelle importante dans des situations plus complexes d’ajustement de courbes et de surfaces. (Cette généralisation, qui sera abordée dans la partie 8, n’est pas équivalente à un test t.)
La répartition de SCTot en ses parties, SCR et SCE et le calcul de la staitistique 7.2.5.4 peuvent être organisés sous la forme d’un tableau d’ANOVA. Le tableau 7.2.5.1 présente le format général utilisé dans cet ouvrage dans le contexte de la régression linéaire simple.

Exemple 7.2.5.1 (suite)
Reprenons la discussion sur l’exemple de la pression et de densité du module 7.1.1. Nous avions alors
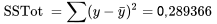
et
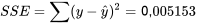
Par conséquent,

et le tableau 7.2.5.1 pour le présent exemple correspond au tableau 7.2.5.2.
Le niveau de signification observé pour tester 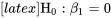 est
est
 717\right]717\right]
717\right]717\right]
et l’on dispose de preuves très solides contre la possibilité que 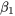 . Un terme linéaire en pression contribue de manière importante à la description de la densité du cylindre. Ce résultat est tout à fait cohérent avec l’analyse précédente axée sur les intervalles, qui a donné des limites de confidence de 95 % pour
. Un terme linéaire en pression contribue de manière importante à la description de la densité du cylindre. Ce résultat est tout à fait cohérent avec l’analyse précédente axée sur les intervalles, qui a donné des limites de confidence de 95 % pour 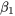 de
de

Cet intervalle ne contient pas 0.
La valeur de 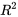 (trouvée la première fois dans le module 7) peut également être facilement obtenue à partir des entrées du tableau 7.2.5.2 et de la relation 7.2.5.1.
(trouvée la première fois dans le module 7) peut également être facilement obtenue à partir des entrées du tableau 7.2.5.2 et de la relation 7.2.5.1.