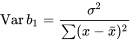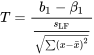7.2.2 Inférence du paramètre de pente
Dans les applications du modèle de régression linéaire simple (équation 7.2.1.1) où  représente une variable qui peut être physiquement manipulée, le paramètre de pente
représente une variable qui peut être physiquement manipulée, le paramètre de pente 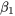 est d’un intérêt fondamental. Il représente le taux de variation de la réponse moyenne par rapport à x et détermine l’incidence d’une variation de x sur la sortie du système. L’inférence de
est d’un intérêt fondamental. Il représente le taux de variation de la réponse moyenne par rapport à x et détermine l’incidence d’une variation de x sur la sortie du système. L’inférence de 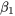 est assez simple, parce que
est assez simple, parce que 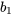 (la pente de la droite des moindres carrés) hérite des propriétés de distribution du modèle. Ainsi, selon le modèle 7.2.1.1,
(la pente de la droite des moindres carrés) hérite des propriétés de distribution du modèle. Ainsi, selon le modèle 7.2.1.1, 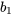 suit une distribution normale avec
suit une distribution normale avec
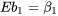
et
7.2.2.1
ce qui signifie que
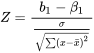
suit une distribution normale réduite. D’une manière similaire à de nombreux arguments des parties 5 et 6, cela explique le fait que la quantité
7.2.2.2
suit une distribution 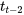 . Les arguments standard de la partie 5 appliqués à l’expression 7.2.2.2 montrent alors que
. Les arguments standard de la partie 5 appliqués à l’expression 7.2.2.2 montrent alors que
7.2.2.3
peut être testée à l’aide de la statistique de test (aussi appelée variable de décision)
7.2.2.4 Statistique de test pour 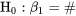
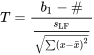
et une distribution de référence 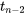 . Plus important encore, dans le cadre du modèle de régression
. Plus important encore, dans le cadre du modèle de régression
linéaire simple (équation 7.2.1.2), un intervalle de confiance bilatéral pour 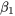 peut être établi avec
peut être établi avec
les bornes suivantes :
7.2.2.5 Limites de confiance pour la pente 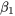
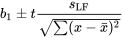
où le niveau de confiance associé correspond à la probabilité assignée à l’intervalle entre 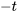 et
et  dans la distribution
dans la distribution 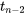 . Un intervalle de confiance unilatéral est établi de la manière habituelle, en utilisant une seule borne dans l’équation 7.2.2.5.
. Un intervalle de confiance unilatéral est établi de la manière habituelle, en utilisant une seule borne dans l’équation 7.2.2.5.
Exemple 7.2.2.1 Étude sur le pressage de la poudre (suite)
Dans l’étude du pressage de poudre, nous avons vu au module 7.1 que la pente de la droite des moindres carrés passant par les données de pression et de densité est la suivante :
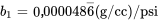
Un intervalle de confiance bilatéral de 95 % pour 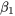 peut être établi en utilisant le quantile 0,975 de la distribution
peut être établi en utilisant le quantile 0,975 de la distribution 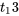 dans l’équation 7.2.2.5. On peut donc utiliser les bornes
dans l’équation 7.2.2.5. On peut donc utiliser les bornes
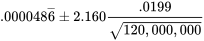
soit
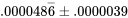
ou

Un intervalle de confidence comme celui-ci de 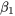 peut être converti en un intervalle de confiance pour une différence de réponses moyennes pour deux valeurs différentes de x. Selon le modèle 7.2.1.2, deux valeurs de
peut être converti en un intervalle de confiance pour une différence de réponses moyennes pour deux valeurs différentes de x. Selon le modèle 7.2.1.2, deux valeurs de  qui diffèrent de
qui diffèrent de 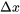 ont des réponses moyennes qui diffèrent de
ont des réponses moyennes qui diffèrent de 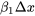 . Pour obtenir un intervalle de confidence pour la différence des réponses moyennes, il suffit alors de multiplier les bornes de l’intervalle de confidence pour
. Pour obtenir un intervalle de confidence pour la différence des réponses moyennes, il suffit alors de multiplier les bornes de l’intervalle de confidence pour 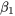 par
par 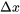 . Par exemple, puisque 8 000 – 6 000 = 2 000, la différence entre les densités moyennes à 8 000 psi et à 6 000 psi a un intervalle de confidence de 95 % avec les bornes
. Par exemple, puisque 8 000 – 6 000 = 2 000, la différence entre les densités moyennes à 8 000 psi et à 6 000 psi a un intervalle de confidence de 95 % avec les bornes
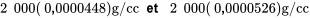
soit
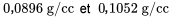
Points à prendre en considération pour la sélection des valeurs de x
L’équation 7.2.2.5 indique la précision de la pente de la droite des moindres carrés. Il est utile de se demander comment cette précision est liée aux caractéristiques de l’étude qu’on peut potentiellement contrôler. Les équations 7.2.2.1 et 7.2.2.5 indiquent toutes deux que plus 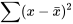 est élevée (c’est-à-dire plus les valeurs
est élevée (c’est-à-dire plus les valeurs 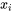 sont dispersées), plus
sont dispersées), plus 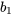 est une estimation précise de la pente sous-jacente
est une estimation précise de la pente sous-jacente 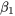 . Ainsi, pour estimer
. Ainsi, pour estimer 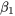 , dans les études où
, dans les études où  représente la valeur d’une variable de système contrôlable, il convient de choisir les paramètres de
représente la valeur d’une variable de système contrôlable, il convient de choisir les paramètres de  ayant la plus grande variance d’échantillon possible. (En fait, si l’on dispose de
ayant la plus grande variance d’échantillon possible. (En fait, si l’on dispose de 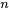 observations à utiliser et que l’on peut choisir des valeurs de
observations à utiliser et que l’on peut choisir des valeurs de  n’importe où dans un intervalle
n’importe où dans un intervalle ![[a,b] [a,b]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/ea5dfda1db89d7e61cb60979bb300cc6.png) , en prendre
, en prendre 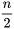 à
à 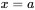 et
et 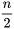 à
à 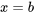 donne la meilleure précision possible pour estimer la pente
donne la meilleure précision possible pour estimer la pente 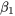 .)
.)
Toutefois, ce conseil (éloigner les 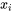 ) doit être pris avec un grain de sel. La relation approximativement linéaire (équation 7.2.1.2) peut ne s’appliquer qu’à une plage limitée de valeurs de x. Si on veut obtenir une bonne estimation de la pente, il est évidemment insensé de choisir des valeurs expérimentales de x au-delà des limites où l’on peut raisonnablement s’attendre à ce que l’équation 7.2.1.2 s’applique. Il est également important de comprendre que l’estimation précise de
) doit être pris avec un grain de sel. La relation approximativement linéaire (équation 7.2.1.2) peut ne s’appliquer qu’à une plage limitée de valeurs de x. Si on veut obtenir une bonne estimation de la pente, il est évidemment insensé de choisir des valeurs expérimentales de x au-delà des limites où l’on peut raisonnablement s’attendre à ce que l’équation 7.2.1.2 s’applique. Il est également important de comprendre que l’estimation précise de 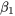 reposant sur les hypothèses du modèle 7.2.1.2 n’est pas le seul élément à prendre en considération lors de la planification de la collecte des données. Il est généralement aussi important d’être en mesure de dire quand la forme linéaire de l’équation 7.2.1.2 est inappropriée. Pour cela, il faut recueillir des données pour un plusieurs valeurs différentes de
reposant sur les hypothèses du modèle 7.2.1.2 n’est pas le seul élément à prendre en considération lors de la planification de la collecte des données. Il est généralement aussi important d’être en mesure de dire quand la forme linéaire de l’équation 7.2.1.2 est inappropriée. Pour cela, il faut recueillir des données pour un plusieurs valeurs différentes de  , et non pas simplement pour les valeurs les plus faibles et les plus élevées
, et non pas simplement pour les valeurs les plus faibles et les plus élevées
possibles.