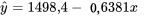7.1.3 Calcul et utilisation des résidus
Lorsqu’on ajuste une équation à un ensemble de données, on espère que l’équation extrait le message principal des données, ne laissant derrière elle que la variation de y qui est ininterprétable (non prédite par l’équation ajustée). En d’autres mots, on espère que les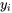 
ressembleront aux 
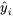, sauf pour de petites fluctuations qui ne peuvent être expliquées que par des variations aléatoires. Une façon d’évaluer si ce point de vue est raisonnable consiste à calculer et à tracer les résidus.
DÉFINITION Résidus
EXPRESSION 7.1.3.1
Si l’ajustement d’une équation ou d’un modèle à un ensemble de données comportant des réponses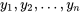 
donne des valeurs ajustées 
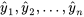, les résidus correspondants ont alors les valeurs suivantes :
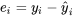
Si une équation ajustée raconte toute l’histoire d’un ensemble de données, alors ses résidus devraient être dépourvus de toute tendance. Ainsi, lorsqu’ils sont tracés en fonction de l’ordre chronologique d’observation, des valeurs des variables expérimentales, des valeurs ajustées ou de toute autre valeur raisonnable, les tracés doivent être dispersés de manière aléatoire. Lorsque ce n’est pas le cas, les tendances peuvent elles-mêmes suggérer ce qui n’a pas été pris en compte lors de l’ajustement ou la manière dont la synthèse des données pourrait être améliorée.
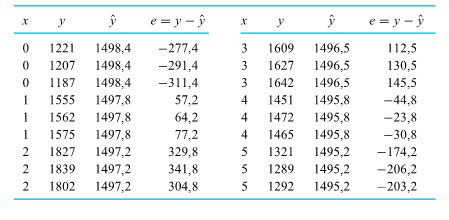
Exemple 7.1.3.1 Résistance à la compression de cylindres en béton de cendres volantes en fonction de la quantité d’additif de phosphate d’ammonium
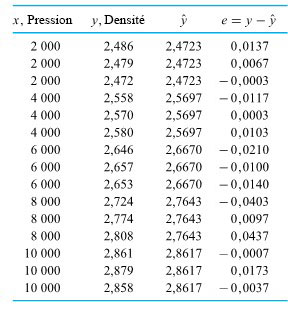
Pour illustrer de façon exagérée le point précédent, examinons l’ajustement simpliste d’une droite sur certaines données réalisé par B. Roth, qui a étudié la résistance à la compression de cylindres en béton de cendres volantes. Ces cylindres ont été fabriqués en utilisant des quantités variables de phosphate d’ammonium comme additif. Une partie de ses données est présentée dans le tableau 7.1.3.1. Les valeurs de phosphate d’ammonium sont exprimées en pourcentage du poids de la quantité de cendres volantes utilisée.
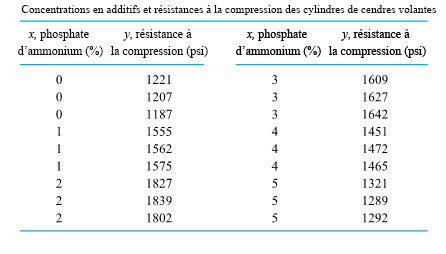
En utilisant les formules 7.1.1.5 et 7.1.1.6, il est possible de montrer que la droite des moindres carrés qui passe par les points (x, y) du tableau 7.1.3.1 est :
7.1.3.2
Une substitution directe dans l’équation 7.1.3.2 donne les valeurs 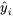et les résidus 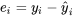, comme indiqué dans le tableau 7.1.3.2. La figure 7.1.3.1 montre les résidus de cette régression linéaire en fonction de x.
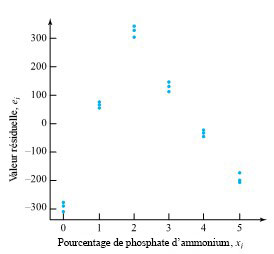
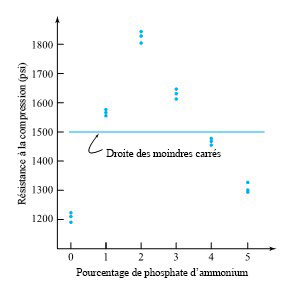
Interprétation des tendances des tracés résiduels
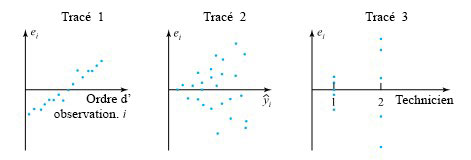
La figure 7.1.3.3 présente quelques tendances qui peuvent être observées dans les tracés des résidus en fonction de diverses variables. Le graphique 1 de la figure 7.1.3.3 montre une tendance du tracé des résidus en fonction de l’ordre chronologique d’observation. Cette tendance suggère qu’une variable changeant dans le temps agit sur y et n’a pas été prise en compte dans les valeurs d’ajustement. Par exemple, la dérive instrumentale (lorsqu’un instrument affiche une valeur plus élevée à la fin d’une analyse qu’au début) pourrait produire une tendance comme celle du graphique 1. Le graphique 2 montre un modèle en forme d’éventail sur un tracé des résidus par rapport aux valeurs ajustées. Une telle tendance indique que les valeurs élevées sont ajustées (et très probablement produites ou mesurées) de manière moins uniforme que les valeurs faibles. Le graphique 3 montre des résidus correspondant à des observations faites par l’ingénieur.e 1 qui sont dans l’ensemble plus faibles que celles faites par l’ingénieur.e 2. On peut en déduire que le travail de l’ingénieur.e 1 est plus précis que celui de l’ingénieur.e 2.
Tracé normal des résidus
Une autre façon utile de tracer les résidus est de les représenter sous forme de graphique normal. L’idée est que la forme de la distribution normale est caractéristique de la variation aléatoire et que le tracé normal des résidus est un moyen de vérifier si cette forme de distribution s’applique à ce qui reste des données après l’ajustement d’une équation ou d’un modèle.
Exemple 7.1.3.2 (suite)
Le tableau 7.1.3.3 donne les résidus pour l’ajustement d’une droite aux données relatives à la pression et à la densité. Les résidus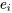 
ont été traités comme un échantillon de 15 nombres et ont été tracés de façon normale (en utilisant les méthodes que nous avons présentées précédemment) pour donner la figure 7.1.3.4.
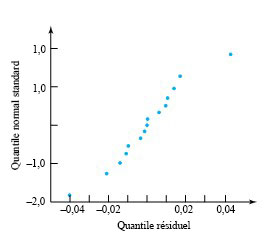
La partie centrale du graphique de la figure 7.1.3.4 est assez linéaire, indiquant une distribution des résidus généralement en forme de cloche. Mais le point tracé correspondant au résidu le plus élevé, et probablement celui correspondant au résidu le plus faible, ne suivent pas le modèle linéaire établi par les autres. Comparés aux autres, ces résidus semblent plutôt importants.
Le tableau 7.1.3.3 et le nuage de points de la figure 7.1.1.3 montrent que ces résidus élevés proviennent tous deux de la pression de 8 000 psi. De plus, l’écart pour les trois densités à cette valeur de pression semble en effet considérablement plus important que pour les autres valeurs de pression. Le tracé normal laisse supposer que la tendance de la variation à 8 000 psi est véritablement différente de celle observée aux autres pressions. Il est possible qu’un mécanisme physique de compression différent ait agi à 8 000 psi par rapport aux autres pressions. Cependant, il est plus probable qu’il y ait eu un problème de technique de laboratoire, d’enregistrement ou de matériel d’essai lorsque les essais à 8 000 psi ont été effectués.
Quoi qu’il en soit, le tracé normal des résidus permet de mettre en évidence une particularité des données du tableau 7.1.1.1 qui mérite d’être approfondie et, peut-être, de faire l’objet d’une nouvelle collecte de données.
ajustement linéaire aux données de pression et de la densité.