7.1.2 Corrélation d’échantillon et coefficient de détermination
Corrélation
Visuellement, la droite des moindres carrés de la figure 7.1.1.3 semble bien correspondre aux points indiqués. Cependant, il serait utile de disposer de méthodes permettant de quantifier la qualité de cette régression. L’une de ces méthodes est la corrélation d’échantillon.
DÉFINITION Corrélation (linéaire) d’échantillon
EXPRESSION 7.1.2.1
La corrélation (linéaire) d’échantillon entre x et y dans un échantillon de n paires de données 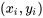 est
est
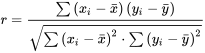
Interprétation de la corrélation d’échantillon
La corrélation d’échantillon se situe toujours entre -1 et 1 inclusivement. Elle est égale à -1 ou à 1 uniquement lorsque tous les points de données (x , y) se situent sur une même ligne droite. En comparant les équations 7.1.1.5 et 7.1.2.1, on constate que 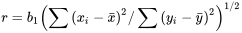 , ce qui indique que
, ce qui indique que 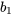 et
et 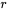 ont le même signe. Ainsi, une corrélation d’échantillon de -1 signifie que y diminue de façon linéaire lorsque x augmente, tandis qu’une corrélation d’échantillon de +1 signifie que y augmente de façon linéaire lorsque x augmente.
ont le même signe. Ainsi, une corrélation d’échantillon de -1 signifie que y diminue de façon linéaire lorsque x augmente, tandis qu’une corrélation d’échantillon de +1 signifie que y augmente de façon linéaire lorsque x augmente.
Les ensembles de données réelles sont rarement en corrélation parfaite (+1 ou -1). La valeur de r est généralement comprise entre -1 et 1. Mais en se basant sur les faits relatifs à son comportement, on considère r comme une mesure de la force d’une relation linéaire apparente : un r proche de +1 ou -1 est interprété comme indiquant une relation linéaire relativement forte, et un r proche de 0, comme indiquant une absence de relation linéaire. Le signe de r indique si y tend à augmenter ou à diminuer lorsque x augmente.
Exemple 7.1.2.2 (suite)
Pour les données relatives à la pression et à la densité, les données récapitulatives de l’exemple donnent :
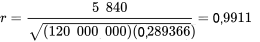
Cette valeur de r est proche de +1 et indique clairement la forte relation linéaire positive mise en évidence dans les figures 7.1.1.1 et 7.1.1.3.
Coefficient de détermination
DÉFINITION Coefficient de détermination
EXPRESSION 7.1.2.2
Pour une équation de régression d’un ensemble de données de n points obtenue par la méthode des moindres carrés produisant des valeurs ajustées  , le coefficient de détermination vaut :
, le coefficient de détermination vaut :
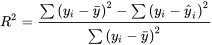
Interprétation de 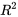
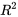 peut être interprétée comme la fraction de la variation brute de y prise en compte par l’équation ajustée, à condition que l’équation ajustée comprenne une constante,
peut être interprétée comme la fraction de la variation brute de y prise en compte par l’équation ajustée, à condition que l’équation ajustée comprenne une constante, 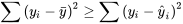 . De plus,
. De plus, 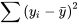 est une mesure de la variabilité brute de y, tandis que
est une mesure de la variabilité brute de y, tandis que 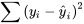 est une mesure de la variation de y restante après la régression de l’équation. La différence non négative
est une mesure de la variation de y restante après la régression de l’équation. La différence non négative 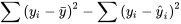 est donc une mesure de la variabilité de y prise en compte dans le processus de régression.
est donc une mesure de la variabilité de y prise en compte dans le processus de régression. 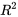 exprime cette différence sous forme de fraction (de la variation brute totale).
exprime cette différence sous forme de fraction (de la variation brute totale).
Exemple 7.1.2.2 (suite)
En utilisant la droite de régression, on peut trouver les valeurs 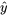 pour tous les n = 15 points de données de l’ensemble de données d’origine. Ces valeurs sont indiquées dans le tableau 7.1.2.1.
pour tous les n = 15 points de données de l’ensemble de données d’origine. Ces valeurs sont indiquées dans le tableau 7.1.2.1.
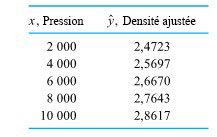
Ensuite, en se reportant à nouveau au tableau 7.1.1.1,
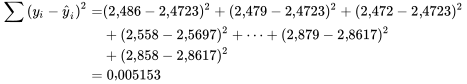
De plus, puisque 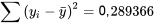 , l’équation 7.1.2.2 donne :
, l’équation 7.1.2.2 donne :
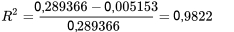
Ainsi, la droite de régression représente plus de 98 % de la variabilité brute de la densité, réduisant la variation « inexpliquée » de 0,289366 à 0,005153.
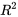 en tant que corrélation quadratiqueLe coefficient de détermination a une deuxième interprétation utile. Pour les équations dont les paramètres sont linéaires (qui sont les seules pris en compte ici et qui seront abordées en détail ultérieurement),
en tant que corrélation quadratiqueLe coefficient de détermination a une deuxième interprétation utile. Pour les équations dont les paramètres sont linéaires (qui sont les seules pris en compte ici et qui seront abordées en détail ultérieurement), 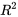 s’avère être une corrélation quadratique entre les valeurs observées
s’avère être une corrélation quadratique entre les valeurs observées 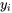 et les valeurs ajustées
et les valeurs ajustées 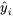 . (Dans la régression linéaire –le cas qui nous intéresse en ce moment –, les valeurs
. (Dans la régression linéaire –le cas qui nous intéresse en ce moment –, les valeurs 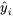 sont parfaitement corrélées avec les valeurs
sont parfaitement corrélées avec les valeurs 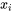 ,
, 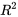 est donc également la corrélation quadratique entre les valeurs
est donc également la corrélation quadratique entre les valeurs 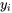 et
et 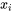 .)
.)
Exemple 7.1.2.3 (suite)
Pour les données relatives à la pression et à la densité, la corrélation entre x et y est la suivante :
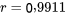
Puisque 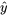 est parfaitement corrélé avec x, c’est aussi la corrélation entre
est parfaitement corrélé avec x, c’est aussi la corrélation entre 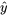 et
et  . Notons également que
. Notons également que
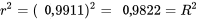
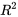 est bien la corrélation d’échantillon quadratique entre
est bien la corrélation d’échantillon quadratique entre  et
et 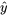 .
.
