7.1.0 Introduction aux moindres carrés : description de la relation entre des données quantitatives à deux variables

Les données à deux variables résultent souvent du fait qu’une variable quantitative expérimentale x dépend de plusieurs paramètres, ce qui produit plusieurs d’échantillons d’une variable de réponse y. Aux fins de la réduction des données, de l’interpolation, de l’extrapolation limitée, ou encore de l’optimisation ou de l’ajustement du processus, il est extrêmement utile d’avoir une équation reliant y à x. Une équation linéaire de la forme

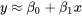
qui relie y à x est l’équation la plus simple potentiellement utile à envisager après avoir fait un nuage de points (x, y) simple.

Dans ce chapitre, la méthode des moindres carrés est utilisée pour tracer une droite de régression correspondant aux données (x, y). L’exactitude de cette régression est évaluée à l’aide de la corrélation de l’échantillon et du coefficient de détermination. La représentation graphique des résidus est présentée comme une méthode importante pour approfondir l’étude des problèmes éventuels liés à la droite de régression. Une discussion sur certaines mises en garde pratiques et sur l’utilisation de logiciels statistiques pour les droites
de régression suit.