6.3.3 Identité et tableau d’ANOVA à un facteur
 nombres
nombres 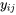 :
: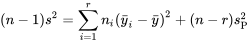
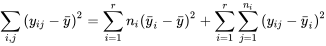
.
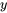 , à savoir
, à savoir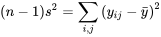
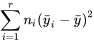
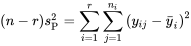
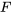 6.3.2.3, conçue pour tester
6.3.2.3, conçue pour tester 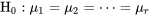 , le numérateur se rapporte à la première des deux, et le dénominateur à la deuxième. Utiliser la statistique
, le numérateur se rapporte à la première des deux, et le dénominateur à la deuxième. Utiliser la statistique 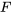 de l’ANOVA revient presque à analyser la variabilité brute de
de l’ANOVA revient presque à analyser la variabilité brute de 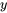 .
.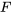 de l’ANOVA à un facteur et leur utilité en tant que statistiques descriptives à part entière, on attribue généralement un nom spécifique et une abréviation aux trois sommes (des carrés) figurant dans les équations 6.3.3.1 et 6.3.3.2, énoncés ci-dessous sous forme de définition :
de l’ANOVA à un facteur et leur utilité en tant que statistiques descriptives à part entière, on attribue généralement un nom spécifique et une abréviation aux trois sommes (des carrés) figurant dans les équations 6.3.3.1 et 6.3.3.2, énoncés ci-dessous sous forme de définition :DÉFINITION 6.3.3.1 Somme totale des carrés SCTot
Dans une étude multi-échantillons, la somme des carrés des différences entre les valeurs des données brutes et la moyenne du grand échantillon, 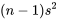 , est appelée somme totale des carrés et notée SCTot.
, est appelée somme totale des carrés et notée SCTot.
DÉFINITION 6.3.3.2 Somme des carrés des traitements SCTr
Dans une étude multi-échantillons non structurée, la somme 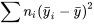 est appelée somme des carrés des traitements et notée SCTr.
est appelée somme des carrés des traitements et notée SCTr.
DÉFINITION 6.3.3.3 Somme des carrés d’erreur résiduelle SCE
Dans une étude multi-échantillons, la somme des carrés des résidus, 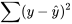 (qui équivaut à
(qui équivaut à 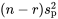 dans un cas non structuré) est appelée somme des carrés d’erreur résiduelle et notée SCE.
dans un cas non structuré) est appelée somme des carrés d’erreur résiduelle et notée SCE.
.
Dans la nouvelle notation présentée dans ces définitions, la proposition 6.3.3.1 énonce que dans un cadre multi-échantillons non structuré :
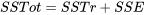
.
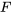 de l’équation 6.3.2.3 et, d’autre part, de consolider et d’élargir l’intuition au sujet de la variance fournie par les équations 6.3.3.1, 6.3.3.2 et 6.3.3.3. Il existe de nombreuses formes de tables d’analyse de la variance correspondant à des analyses multi-échantillons diverses et variées. La plus judicieuse à utiliser dans le cas présent est celle représentée sous forme symbolique dans le tableau 6.3.3.1.
de l’équation 6.3.2.3 et, d’autre part, de consolider et d’élargir l’intuition au sujet de la variance fournie par les équations 6.3.3.1, 6.3.3.2 et 6.3.3.3. Il existe de nombreuses formes de tables d’analyse de la variance correspondant à des analyses multi-échantillons diverses et variées. La plus judicieuse à utiliser dans le cas présent est celle représentée sous forme symbolique dans le tableau 6.3.3.1.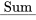 des
des 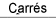 SS (de la source), degrés de liberté df (de la source), carré de la moyenne MS (de la source), et
SS (de la source), degrés de liberté df (de la source), carré de la moyenne MS (de la source), et 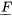 (pour le test d’hypothèse de la contribution de la source dans la variabilité globale observée). Dans la colonne Source du tableau, les entrées sont Traitements, Erreur et Total. Mais le terme « traitements » peut parfois être remplacé par « inter (échantillons) », et « Erreur » par « intra (échantillons) » ou « résiduel ». La somme des deux premières entrées de la colonne SC (SS) doit correspondre à la troisième, comme indiqué par l’équation 6.3.3.3. De même, la somme des degrés de liberté pour les traitements et l’erreur donne le nombre total de degrés de liberté,
(pour le test d’hypothèse de la contribution de la source dans la variabilité globale observée). Dans la colonne Source du tableau, les entrées sont Traitements, Erreur et Total. Mais le terme « traitements » peut parfois être remplacé par « inter (échantillons) », et « Erreur » par « intra (échantillons) » ou « résiduel ». La somme des deux premières entrées de la colonne SC (SS) doit correspondre à la troisième, comme indiqué par l’équation 6.3.3.3. De même, la somme des degrés de liberté pour les traitements et l’erreur donne le nombre total de degrés de liberté, 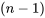 . À noter que les entrées de la colonne
. À noter que les entrées de la colonne 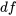 sont respectivement liées au numérateur et au dénominateur de la statistique de test dans l’équation 6.3.2.3. Les rapports entre les sommes des carrés et les degrés de liberté sont appelés carrés de moyennes; ici, le carré de la moyenne pour les traitements (MSTr) et le carré de la moyenne pour l’erreur (MSE). Dans le cas présent, il faut vérifier que
sont respectivement liées au numérateur et au dénominateur de la statistique de test dans l’équation 6.3.2.3. Les rapports entre les sommes des carrés et les degrés de liberté sont appelés carrés de moyennes; ici, le carré de la moyenne pour les traitements (MSTr) et le carré de la moyenne pour l’erreur (MSE). Dans le cas présent, il faut vérifier que 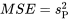 et que
et que 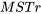 est le numérateur de la statistique
est le numérateur de la statistique 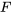 de l’équation 6.3.2.3. Le rapport apparaissant dans la colonne
de l’équation 6.3.2.3. Le rapport apparaissant dans la colonne 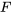 est donc la valeur observée de
est donc la valeur observée de 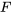 pour le test
pour le test 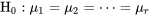 .
.
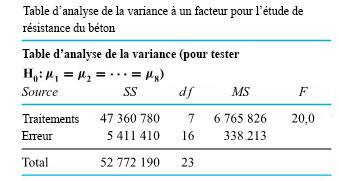
Exemple 6.3.3.1 Étude sur la résistance du béton (suite)
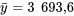 , donc
, donc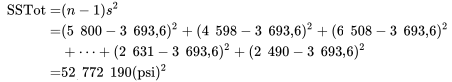
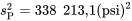 et
et 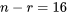 , on a donc :
, on a donc :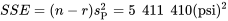
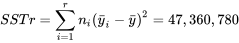
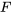 , les degrés de liberté et les valeurs de
, les degrés de liberté et les valeurs de 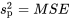 .
.