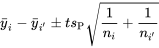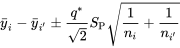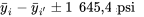6.2.3 Méthodes d’intervalles de confiance simultanés
Comme l’explique la section 6.2.2, dans le cadre d’une étude multi-échantillons, on peut créer plusieurs types d’intervalles de confiance pour des moyennes ou des combinaisons linéaires de moyennes. On y a aussi parlé du problème des niveaux de confiance individuels plutôt que simultanés, mais le seul moyen mentionné pour obtenir un niveau simultané était d’utiliser l’inégalité de Bonferroni.
.
Cette section présente une méthode permettant de créer divers intervalles de confiance et de maintenir un niveau de confiance simultané au cours du processus. Il s’agit de la méthode de Tukey pour l’estimation d’intervalles de confiance simultanés de toutes les différences deux à deux entre les moyennes sous-jacentes.
Méthode de Tukey
Souvent, dans les études à  échantillons, on s’intéresse aussi aux différences entre les
échantillons, on s’intéresse aussi aux différences entre les 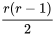 paires de réponses moyennes
paires de réponses moyennes 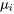 et
et 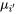 . La section 6.2 affirme qu’estimer une différence unique entre les réponses de moyenne
. La section 6.2 affirme qu’estimer une différence unique entre les réponses de moyenne 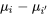 est possible à l’aide d’un intervalle ayant pour bornes
est possible à l’aide d’un intervalle ayant pour bornes
 échantillons, on s’intéresse aussi aux différences entre les
échantillons, on s’intéresse aussi aux différences entre les 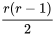 paires de réponses moyennes
paires de réponses moyennes 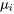 et
et 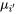 . La section 6.2 affirme qu’estimer une différence unique entre les réponses de moyenne
. La section 6.2 affirme qu’estimer une différence unique entre les réponses de moyenne 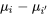 est possible à l’aide d’un intervalle ayant pour bornes
est possible à l’aide d’un intervalle ayant pour bornes.
6.2.3.1
.
où le niveau de confiance associé est individuel. Mais si, par exemple, 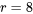 , il y a 28 différentes comparaisons deux à deux de moyennes sous-jacentes à prendre en compte (
, il y a 28 différentes comparaisons deux à deux de moyennes sous-jacentes à prendre en compte ( 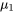 et
et 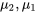 et
et 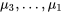 et
et 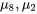 et
et 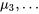 , et
, et 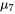 et
et 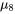 ). Si on veut garantir un niveau de confiance simultané raisonnable pour toutes ces comparaisons en utilisant l’inégalité rudimentaire de Bonferroni, il faut un très haut niveau de confiance individuel pour les intervalles 6.2.3.1. Par exemple, avec 28 intervalles, il faut un niveau de confiance de
). Si on veut garantir un niveau de confiance simultané raisonnable pour toutes ces comparaisons en utilisant l’inégalité rudimentaire de Bonferroni, il faut un très haut niveau de confiance individuel pour les intervalles 6.2.3.1. Par exemple, avec 28 intervalles, il faut un niveau de confiance de 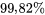 pour pouvoir garantir un niveau de confiance simultané de
pour pouvoir garantir un niveau de confiance simultané de 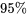 .
.
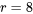 , il y a 28 différentes comparaisons deux à deux de moyennes sous-jacentes à prendre en compte (
, il y a 28 différentes comparaisons deux à deux de moyennes sous-jacentes à prendre en compte ( 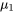 et
et 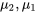 et
et 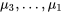 et
et 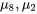 et
et 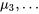 , et
, et 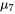 et
et 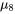 ). Si on veut garantir un niveau de confiance simultané raisonnable pour toutes ces comparaisons en utilisant l’inégalité rudimentaire de Bonferroni, il faut un très haut niveau de confiance individuel pour les intervalles 6.2.3.1. Par exemple, avec 28 intervalles, il faut un niveau de confiance de
). Si on veut garantir un niveau de confiance simultané raisonnable pour toutes ces comparaisons en utilisant l’inégalité rudimentaire de Bonferroni, il faut un très haut niveau de confiance individuel pour les intervalles 6.2.3.1. Par exemple, avec 28 intervalles, il faut un niveau de confiance de 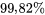 pour pouvoir garantir un niveau de confiance simultané de
pour pouvoir garantir un niveau de confiance simultané de 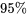 .
..
Une meilleure approche pour définir les limites de confiance simultanées pour toutes les différences 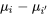 est de remplacer
est de remplacer  dans la formule 6.2.3.1 par un multiplicateur obtenu expressément afin de fournir un niveau de confiance simultané pour l’estimation de ce genre de différences. C’est J. Tukey qui a expliqué qu’il était possible de trouver de tels multiplicateurs en utilisant les quantiles de distributions d’intervalles studentisés. Les tables A5A et A5B donnent les valeurs des constantes
dans la formule 6.2.3.1 par un multiplicateur obtenu expressément afin de fournir un niveau de confiance simultané pour l’estimation de ce genre de différences. C’est J. Tukey qui a expliqué qu’il était possible de trouver de tels multiplicateurs en utilisant les quantiles de distributions d’intervalles studentisés. Les tables A5A et A5B donnent les valeurs des constantes 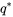 , de sorte que l’ensemble d’intervalles bilatéraux ayant pour bornes
, de sorte que l’ensemble d’intervalles bilatéraux ayant pour bornes
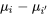 est de remplacer
est de remplacer  dans la formule 6.2.3.1 par un multiplicateur obtenu expressément afin de fournir un niveau de confiance simultané pour l’estimation de ce genre de différences. C’est J. Tukey qui a expliqué qu’il était possible de trouver de tels multiplicateurs en utilisant les quantiles de distributions d’intervalles studentisés. Les tables A5A et A5B donnent les valeurs des constantes
dans la formule 6.2.3.1 par un multiplicateur obtenu expressément afin de fournir un niveau de confiance simultané pour l’estimation de ce genre de différences. C’est J. Tukey qui a expliqué qu’il était possible de trouver de tels multiplicateurs en utilisant les quantiles de distributions d’intervalles studentisés. Les tables A5A et A5B donnent les valeurs des constantes 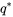 , de sorte que l’ensemble d’intervalles bilatéraux ayant pour bornes
, de sorte que l’ensemble d’intervalles bilatéraux ayant pour bornes.
6.2.3.2 Limites de confiance simultanées bilatérales de Tukey pour toutes les différences entremoyennes
.
présente un niveau de confiance simultané d’au moins 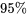 ou
ou 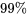 (selon si on lit
(selon si on lit 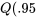 ) dans la table A5A ou
) dans la table A5A ou 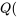 0,99) dans la table A5B) pour l’estimation de toutes les différences
0,99) dans la table A5B) pour l’estimation de toutes les différences 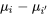 . Si toutes les tailles d’échantillon
. Si toutes les tailles d’échantillon 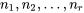 sont les mêmes, le niveau de confiance simultané nominal de
sont les mêmes, le niveau de confiance simultané nominal de 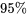 ou
ou 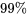 est exact, tandis que si les tailles sont différentes, la valeur réelle est au moins égale à la valeur nominale.
est exact, tandis que si les tailles sont différentes, la valeur réelle est au moins égale à la valeur nominale.
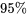 ou
ou 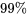 (selon si on lit
(selon si on lit 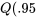 ) dans la table A5A ou
) dans la table A5A ou 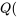 0,99) dans la table A5B) pour l’estimation de toutes les différences
0,99) dans la table A5B) pour l’estimation de toutes les différences 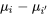 . Si toutes les tailles d’échantillon
. Si toutes les tailles d’échantillon 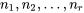 sont les mêmes, le niveau de confiance simultané nominal de
sont les mêmes, le niveau de confiance simultané nominal de 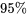 ou
ou 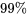 est exact, tandis que si les tailles sont différentes, la valeur réelle est au moins égale à la valeur nominale.
est exact, tandis que si les tailles sont différentes, la valeur réelle est au moins égale à la valeur nominale..
Pour pouvoir appliquer la méthode de Tukey, il faut trouver, dans la table A5 (par interpolation, si nécessaire), la colonne correspondant au nombre d’échantillons ou de moyennes à comparer, ainsi que la ligne correspondant aux degrés de liberté associés à 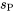 , (à savoir
, (à savoir 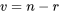 ).
).
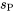 , (à savoir
, (à savoir 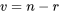 ).
)..
Exemple 6.2.3.1 Résistances à la compression (suite)
La figure 6.2.3.1 représente le graphique de la résistance moyenne à la compression de huit échantillons, avec des barres d’erreur dérivées des limites de confiance simultanées.
Calculons les intervalles de confiance pour les différences de résistances à la compression selon l’échantillon. Si on veut obtenir un intervalle de confiance individuel bilatéral de 95 % pour une différence 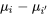 donnée, la formule 6.2.3.1 montre que les bornes adéquates sont
donnée, la formule 6.2.3.1 montre que les bornes adéquates sont
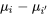 donnée, la formule 6.2.3.1 montre que les bornes adéquates sont
donnée, la formule 6.2.3.1 montre que les bornes adéquates sont.
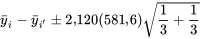
.
soit :
.
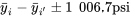
.
En revanche, si on souhaite estimer toutes les différences de résistances moyennes à la compression avec un niveau de confiance simultané de 95 %, l’équation 6.2.3.2 dit que les intervalles bilatéraux de Tukey ont pour bornes
.
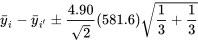
.
soit :
.
.
(Le chiffre 4,90 correspond à la valeur à la colonne 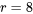 et à la ligne
et à la ligne 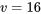 de la table A5A.)
de la table A5A.)
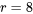 et à la ligne
et à la ligne 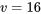 de la table A5A.)
de la table A5A.).
Compte tenu du fait que le niveau de confiance associé aux deuxièmes intervalles est simultané, les intervalles de Tukey sont plus larges que ceux indiqués par la première formule.
.
La partie ± de l’équation finale est moins du double de la partie ± de l’expression précédente. Ainsi, sur la figure 6.3.2.1, il n’est pas nécessaire que les barres d’erreur entourant deux moyennes données ne se chevauchent pas pour pouvoir affirmer qu’on peut détecter une différence entre ces moyennes. Il suffit plutôt que la différence entre deux moyennes d’échantillon soit au moins égale à la partie ± de la formule 6.2.3.2, soit 1 645,4 psi dans le cas présent.
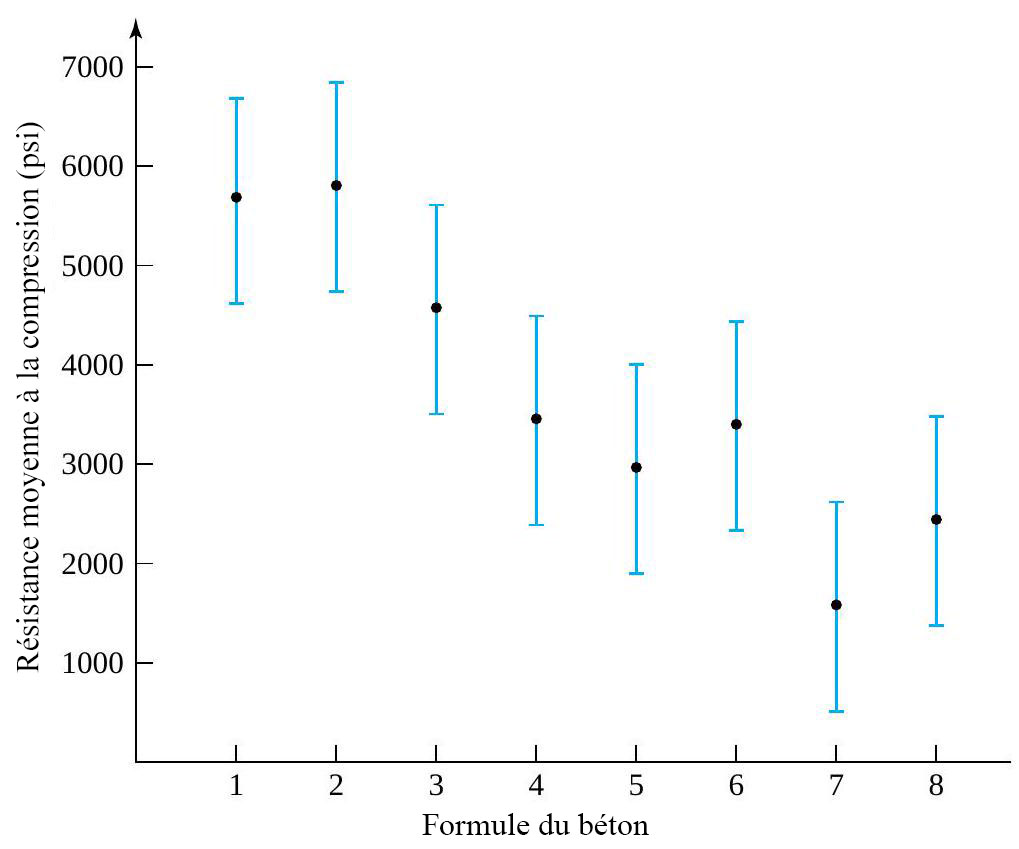
Figure 6.2.3.1 Graphique de la résistance moyenne à la compression de huit échantillons, avec barres d’erreur dérivées des limites de confiance simultanées.