6.2.2 Niveaux de confiance individuels et simultanés
Cette section a présenté des intervalles de confiance divers et variés pour les études multi-échantillons. Nombre d’entre eux peuvent être utilisés dans le cadre d’une application donnée, peut-être même plusieurs à la fois. Par exemple, même dans le cadre relativement simple de l’exemple 6.2.1.1. (étude d’absorption de la serviette en papier), il serait raisonnable de vouloir des intervalles de confiance pour toutes les valeurs suivantes :
.
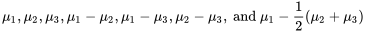
.
Étant donné qu’il faut souvent donner plusieurs estimations de confiance dans les études multi-échantillons, il est important de réfléchir au sens de ces niveaux de confiance et de ne pas oublier qu’ils sont rattachés à un seul intervalle. Autrement dit, si on donne plusieurs intervalles de confiance de 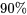 , ce chiffre de
, ce chiffre de 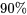 s’applique individuellement à chaque intervalle : on est « à
s’applique individuellement à chaque intervalle : on est « à 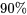 sûr » du premier intervalle, mais aussi « à
sûr » du premier intervalle, mais aussi « à 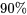 sûr » du deuxième, et également « à
sûr » du deuxième, et également « à 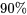 sûr » du troisième, et ainsi de suite. Il est très difficile de savoir comment obtenir un taux de fiabilité conjoint ou simultané pour les intervalles (par exemple une probabilité a priori que tous les intervalles s’appliquent), mais il est assez évident que ce taux doit être inférieur à
sûr » du troisième, et ainsi de suite. Il est très difficile de savoir comment obtenir un taux de fiabilité conjoint ou simultané pour les intervalles (par exemple une probabilité a priori que tous les intervalles s’appliquent), mais il est assez évident que ce taux doit être inférieur à 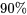 . Le niveau de confiance simultané ou conjoint (le taux de fiabilité global) à associer à un groupe d’intervalles n’est en effet généralement pas facile à déterminer, mais il est typiquement inférieur (et parfois même bien inférieur) au niveau de confiance de chaque intervalle individuel.
. Le niveau de confiance simultané ou conjoint (le taux de fiabilité global) à associer à un groupe d’intervalles n’est en effet généralement pas facile à déterminer, mais il est typiquement inférieur (et parfois même bien inférieur) au niveau de confiance de chaque intervalle individuel.
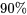 , ce chiffre de
, ce chiffre de 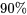 s’applique individuellement à chaque intervalle : on est « à
s’applique individuellement à chaque intervalle : on est « à 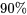 sûr » du premier intervalle, mais aussi « à
sûr » du premier intervalle, mais aussi « à 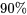 sûr » du deuxième, et également « à
sûr » du deuxième, et également « à 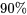 sûr » du troisième, et ainsi de suite. Il est très difficile de savoir comment obtenir un taux de fiabilité conjoint ou simultané pour les intervalles (par exemple une probabilité a priori que tous les intervalles s’appliquent), mais il est assez évident que ce taux doit être inférieur à
sûr » du troisième, et ainsi de suite. Il est très difficile de savoir comment obtenir un taux de fiabilité conjoint ou simultané pour les intervalles (par exemple une probabilité a priori que tous les intervalles s’appliquent), mais il est assez évident que ce taux doit être inférieur à 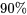 . Le niveau de confiance simultané ou conjoint (le taux de fiabilité global) à associer à un groupe d’intervalles n’est en effet généralement pas facile à déterminer, mais il est typiquement inférieur (et parfois même bien inférieur) au niveau de confiance de chaque intervalle individuel.
. Le niveau de confiance simultané ou conjoint (le taux de fiabilité global) à associer à un groupe d’intervalles n’est en effet généralement pas facile à déterminer, mais il est typiquement inférieur (et parfois même bien inférieur) au niveau de confiance de chaque intervalle individuel..
Maintenant que la différence entre niveaux de confiance simultanés et individuels établie, il existe au moins trois approches possibles. L’option la plus évidente est de créer des intervalles de confiance individuels et de veiller à bien les interpréter comme tels (sachant que plus le nombre
d’intervalles augmente, plus il est probable qu’un ou plusieurs de ces intervalles ne couvrent pas les quantités qu’ils sont censés couvrir).
.
Une autre façon de résoudre le problème de confiance simultanée plutôt qu’individuelle est d’employer des niveaux individuels très élevés pour chaque intervalle, puis d’utiliser une inégalité assez sommaire, l’inégalité de Bonferroni, pour trouver au moins la valeur minimum de confiance simultanée associée au groupe d’intervalles. Cette inégalité indique que si 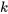 intervalles de confiance ont des niveaux de confiance associés
intervalles de confiance ont des niveaux de confiance associés 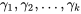 , le niveau de confiance simultané ou conjoint valable pour tous les
, le niveau de confiance simultané ou conjoint valable pour tous les 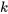 intervalles (disons
intervalles (disons 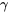 ) satisfait à
) satisfait à
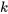 intervalles de confiance ont des niveaux de confiance associés
intervalles de confiance ont des niveaux de confiance associés 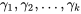 , le niveau de confiance simultané ou conjoint valable pour tous les
, le niveau de confiance simultané ou conjoint valable pour tous les 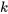 intervalles (disons
intervalles (disons 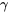 ) satisfait à
) satisfait à.
6.2.2.1 Inégalité de Bonferroni.
.
(Cette inégalité dit essentiellement que la « non-confiance »  conjointe des
conjointe des 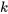 intervalles n’est pas supérieure à la somme des
intervalles n’est pas supérieure à la somme des 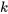 « non-confiances » individuelles. Par exemple, cinq intervalles de niveaux de confiance individuels de
« non-confiances » individuelles. Par exemple, cinq intervalles de niveaux de confiance individuels de 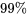 présentent un niveau de confiance conjoint ou simultané d’au moins 95 %.)
présentent un niveau de confiance conjoint ou simultané d’au moins 95 %.)
 conjointe des
conjointe des 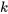 intervalles n’est pas supérieure à la somme des
intervalles n’est pas supérieure à la somme des 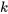 « non-confiances » individuelles. Par exemple, cinq intervalles de niveaux de confiance individuels de
« non-confiances » individuelles. Par exemple, cinq intervalles de niveaux de confiance individuels de 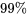 présentent un niveau de confiance conjoint ou simultané d’au moins 95 %.)
présentent un niveau de confiance conjoint ou simultané d’au moins 95 %.).
La troisième façon d’aborder le problème du niveau de confiance simultané est de développer et d’utiliser des méthodes qui, pour certains ensembles spécifiques de quantités inconnues, donnent des intervalles de niveau de confiance simultané connu. Des livres entiers sont consacrés à ce genre de méthodes d’inférence simultanée. La section suivante aborde l’une des plus simples et plus connues.