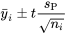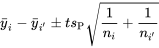6.2.1 Intervalles pour moyennes et comparaison de moyennes
 dans la partie ± des formules d’intervalle – par conséquent, on se retrouve avec de grands intervalles. Mais grâce aux hypothèses du modèle à un facteur, il est possible d’obtenir des formules d’intervalles de confiance qui ont tendance à produire des intervalles plus petits.
dans la partie ± des formules d’intervalle – par conséquent, on se retrouve avec de grands intervalles. Mais grâce aux hypothèses du modèle à un facteur, il est possible d’obtenir des formules d’intervalles de confiance qui ont tendance à produire des intervalles plus petits.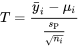
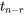 . Par conséquent, l’intervalle de confiance bilatéral pour la
. Par conséquent, l’intervalle de confiance bilatéral pour la  e moyenne,
e moyenne, 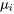 , a pour bornes
, a pour bornes6.2.1.1 Limites de confiance pourbasées sur le modèle à un facteur
.
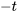 et
et  dans la distribution
dans la distribution 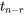 . Il s’agit de la même formule qu’à la partie 5, hormis le fait que
. Il s’agit de la même formule qu’à la partie 5, hormis le fait que 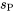 a remplacé
a remplacé 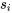 et que les degrés de liberté sont passés de
et que les degrés de liberté sont passés de  à
à  .
. et
et 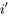 , la variable
, la variable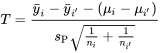
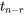 . Par conséquent, l’intervalle de confiance bilatéral pour
. Par conséquent, l’intervalle de confiance bilatéral pour 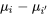 a pour bornes
a pour bornes6.2.1.2 Limites de confiance pourbasées sur le modèle à un facteur
.
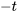 et
et  dans la distribution
dans la distribution 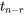 . L’équation 6.2.1.2 reprend essentiellement la formule de la partie 5, hormis le fait que
. L’équation 6.2.1.2 reprend essentiellement la formule de la partie 5, hormis le fait que 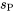 est calculé sur la base de
est calculé sur la base de  échantillons plutôt que deux, et qu’il y a
échantillons plutôt que deux, et qu’il y a  degrés de libertés plutôt que
degrés de libertés plutôt que 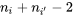 .
.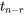 assignée à l’intervalle
assignée à l’intervalle 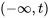 (avec
(avec 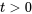 0″ title= »t>0″ class= »latex mathjax »> ). L’avantage des formules 6.2.1.1 et 6.2.1.2 (lorsqu’on peut les appliquer), en comparaison avec les formules correspondantes de la partie 5, c’est que pour un niveau de confiance donné, elles ont tendance à produire des intervalles plus courts.
0″ title= »t>0″ class= »latex mathjax »> ). L’avantage des formules 6.2.1.1 et 6.2.1.2 (lorsqu’on peut les appliquer), en comparaison avec les formules correspondantes de la partie 5, c’est que pour un niveau de confiance donné, elles ont tendance à produire des intervalles plus courts.Exemple 6.2.1.1 Intervalles de confiance pour moyennes et différences de moyennes des résistances à la compression du béton (suite)
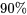 pour la résistance moyenne à la compression d’une seule formule de béton, puis un intervalle de confiance bilatéral de
pour la résistance moyenne à la compression d’une seule formule de béton, puis un intervalle de confiance bilatéral de 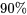 pour la différence de résistance moyenne de deux formules. Étant donné que
pour la différence de résistance moyenne de deux formules. Étant donné que 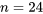 et
et 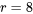 , il y a
, il y a 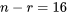 degrés de liberté associés à
degrés de liberté associés à 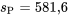 . Le quantile 0,95 de la distribution
. Le quantile 0,95 de la distribution 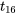 , à savoir 1,746, peut alors être utilisé dans les deux formules 6.2.1.1 et 6.2.1.2.
, à savoir 1,746, peut alors être utilisé dans les deux formules 6.2.1.1 et 6.2.1.2.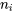 valent 3, la partie ± de la formule 6.2.1.1 donne :
valent 3, la partie ± de la formule 6.2.1.1 donne :
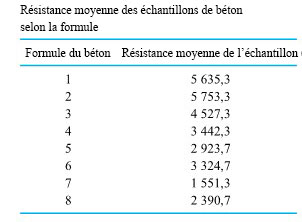
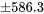 psi pourrait être rattachée à n’importe laquelle des moyennes d’échantillon du Tableau 6.2.1.1 comme estimation de la résistance moyenne de la formule correspondante. Par exemple, comme
psi pourrait être rattachée à n’importe laquelle des moyennes d’échantillon du Tableau 6.2.1.1 comme estimation de la résistance moyenne de la formule correspondante. Par exemple, comme 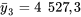 psi, l’intervalle de confiance bilatéral de
psi, l’intervalle de confiance bilatéral de 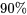 pour
pour 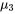 a pour bornes
a pour bornes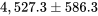

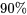 . Là encore, puisque tous les
. Là encore, puisque tous les 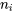 valent 3, la partie ± de la formule 6.2.1.2 donne :
valent 3, la partie ± de la formule 6.2.1.2 donne :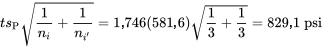
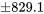 psi pourrait être rattachée à n’importe quelle différence entre les moyennes d’échantillons du tableau 6.2.1.1 comme estimation des résistances moyennes de la différence des formules correspondante. Par exemple, étant donné que
psi pourrait être rattachée à n’importe quelle différence entre les moyennes d’échantillons du tableau 6.2.1.1 comme estimation des résistances moyennes de la différence des formules correspondante. Par exemple, étant donné que 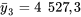 psi et que
psi et que 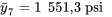 , l’intervalle de confiance bilatéral de
, l’intervalle de confiance bilatéral de 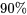 pour
pour  a pour bornes
a pour bornes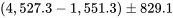
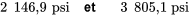
.
L’utilisation de 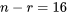 degrés de liberté dans l’exemple 6.2.1.1 plutôt que de
degrés de liberté dans l’exemple 6.2.1.1 plutôt que de 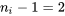 et de
et de 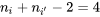 reflète la baisse de l’incertitude associée à l’utilisation de
reflète la baisse de l’incertitude associée à l’utilisation de 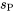 pour estimer
pour estimer 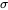 plutôt que l’utilisation de
plutôt que l’utilisation de 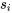 et de
et de 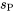 , comme on le faisait avec deux échantillons. Cette réduction de l’incertitude vient avec une condition : elle n’est valide que pour les modèles de variances égales.
, comme on le faisait avec deux échantillons. Cette réduction de l’incertitude vient avec une condition : elle n’est valide que pour les modèles de variances égales.