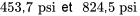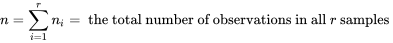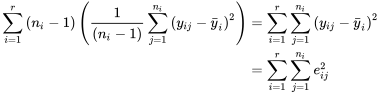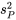6.1.3 Estimation de la variance pondérée pour les études multi-échantillons
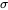 , l’écart-type associé aux réponses des conditions
, l’écart-type associé aux réponses des conditions 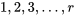 . À l’image de ce qui a été fait dans le cas
. À l’image de ce qui a été fait dans le cas 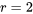 de la partie 5, il est tout à fait typique, dans les études multi-échantillons, de regrouper les variances d’échantillon
de la partie 5, il est tout à fait typique, dans les études multi-échantillons, de regrouper les variances d’échantillon  pour parvenir à une seule estimation de
pour parvenir à une seule estimation de 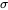 dérivée de tous les
dérivée de tous les  échantillons.
échantillons. échantillons numériques de tailles respectives
échantillons numériques de tailles respectives 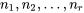 produisent des variances d’échantillons
produisent des variances d’échantillons 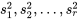 , la variance pondérée,
, la variance pondérée, 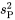 est la moyenne pondérée des variances d’échantillons, où les coefficients de pondération équivalent aux tailles des échantillons moins 1 :
est la moyenne pondérée des variances d’échantillons, où les coefficients de pondération équivalent aux tailles des échantillons moins 1 :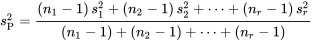
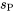 , correspond à la racine carrée de
, correspond à la racine carrée de 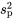 .
..
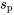 avec deux échantillons,
avec deux échantillons, 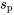 doit se situer entre les valeurs maximum et minimum des
doit se situer entre les valeurs maximum et minimum des 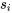 ; c’est une sorte de compromis pratique pour cette valeur sur le plan mathématique.
; c’est une sorte de compromis pratique pour cette valeur sur le plan mathématique.le nombre total d’observations dans le cadre d’une étude à r échantillons
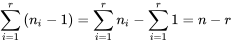
 vaut :
vaut :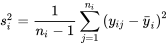
6.1.3.2 et 6.1.3.3
.
Autres formules pour.On peut donc définiren fonction du côté droit de l’équation 6.1.3.2 ou 6.1.3.3 divisé par
.
Exemple 6.1.3.1 Résistance à la compression (suite)
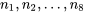 vaut 3, et les valeurs
vaut 3, et les valeurs 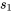 à
à 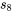 sont données dans le tableau 6.1.2.1. Donc en utilisant l’équation 6.1.3.1,
sont données dans le tableau 6.1.2.1. Donc en utilisant l’équation 6.1.3.1,![\begin{aligned} s_{\mathrm{P}}^2 & =\frac{(3-1)(965,6)^2+(3-1)(432,3)^2+\cdots+(3-1)(302,5)^2}{(3-1)+(3-1)+\cdots+(3-1)} \\ & =\frac{2\left[(965,6)^2+(432,3)^2+\cdots+(302,5)^2\right]}{16 } \\ & =\frac{2 705 705}{8 } \\ & =338 213(\mathrm{psi})^2 \end{aligned} \begin{aligned} s_{\mathrm{P}}^2 & =\frac{(3-1)(965,6)^2+(3-1)(432,3)^2+\cdots+(3-1)(302,5)^2}{(3-1)+(3-1)+\cdots+(3-1)} \\ & =\frac{2\left[(965,6)^2+(432,3)^2+\cdots+(302,5)^2\right]}{16 } \\ & =\frac{2 705 705}{8 } \\ & =338 213(\mathrm{psi})^2 \end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/23f6d727ecf83a1328d7d9195af31d01.png)
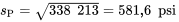
Signification de 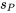
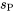 est une estimation de la variation intrinsèque ou de référence d’une variable étudiée pour un ensemble de conditions fixe, calculée en supposant que cette variation de référence est constante dans les conditions dans lesquelles les échantillons ont été prélevés. Lorsque cette supposition est raisonnable, l’idée de la pondération est de combiner plusieurs estimations de petits échantillons (non fiables séparément) pour obtenir une seule estimation relativement plus fiable. C’est une mesure fondamentale très appliquée dans de nombreuses méthodes efficaces d’inférence formelle.
est une estimation de la variation intrinsèque ou de référence d’une variable étudiée pour un ensemble de conditions fixe, calculée en supposant que cette variation de référence est constante dans les conditions dans lesquelles les échantillons ont été prélevés. Lorsque cette supposition est raisonnable, l’idée de la pondération est de combiner plusieurs estimations de petits échantillons (non fiables séparément) pour obtenir une seule estimation relativement plus fiable. C’est une mesure fondamentale très appliquée dans de nombreuses méthodes efficaces d’inférence formelle.
Limites de confiance pour la variance du modèle à un facteur
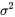 basée sur des données, on a également besoin d’un intervalle de confiance. Avec les restrictions du modèle 6.2.1.1, la variable
basée sur des données, on a également besoin d’un intervalle de confiance. Avec les restrictions du modèle 6.2.1.1, la variable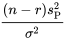
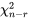 . Ainsi, de la même façon que pour la dérivation de la partie 5, l’intervalle de confiance bilatéral pour [latex]
. Ainsi, de la même façon que pour la dérivation de la partie 5, l’intervalle de confiance bilatéral pour [latex]![\sigma^2[/latex] a pour bornes</div>
<div>.</div>
<blockquote>
<div><strong>6.1.3.4 </strong>[latex]\frac{(n-r) s_{\mathrm{P}}^2}{U} \text { et } \frac{(n-r) s_{\mathrm{P}}^2}{L} \sigma^2[/latex] a pour bornes</div>
<div>.</div>
<blockquote>
<div><strong>6.1.3.4 </strong>[latex]\frac{(n-r) s_{\mathrm{P}}^2}{U} \text { et } \frac{(n-r) s_{\mathrm{P}}^2}{L}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/3250dba6ba9d84059174d0c9a2d8c5fb.png)
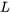 et
et  sont telles que la probabilité
sont telles que la probabilité 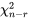 assignée à l’intervalle
assignée à l’intervalle 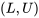 correspond au niveau de confiance souhaité. Et bien sûr, on peut obtenir un intervalle unilatéral en utilisant uniquement l’une des bornes 6.1.3.4 et en choisissant une valeur
correspond au niveau de confiance souhaité. Et bien sûr, on peut obtenir un intervalle unilatéral en utilisant uniquement l’une des bornes 6.1.3.4 et en choisissant une valeur  ou
ou 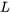 telle que la probabilité
telle que la probabilité 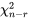 assignée à l’intervalle [latex](0, U)[/latex] ou
assignée à l’intervalle [latex](0, U)[/latex] ou 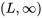 correspond au niveau de confiance souhaité.
correspond au niveau de confiance souhaité.Exemple 6.1.3.2 (suite)
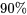 pour
pour 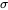 . Étant donné que
. Étant donné que 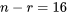 degrés de liberté sont associés à
degrés de liberté sont associés à 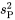 , on consulte le tableau A1.4 pour les quantiles 0,05 et 0,95 de la distribution
, on consulte le tableau A1.4 pour les quantiles 0,05 et 0,95 de la distribution 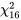 . On lit alors respectivement 7,962 et 26,296. Ainsi, l’intervalle de confiance pour
. On lit alors respectivement 7,962 et 26,296. Ainsi, l’intervalle de confiance pour 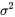 a pour bornes
a pour bornes
 pour
pour 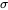 a pour bornes
a pour bornes