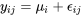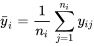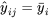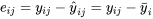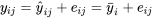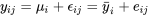6.1.2 Modèle multi-échantillons (normal) à un facteur, valeurs ajustées et résidus
Hypothèses de modèle normal à un facteur
 échantillons, de tailles respectives
échantillons, de tailles respectives 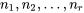 sont indépendants et suivent des distributions normales, avec une variance commune de
sont indépendants et suivent des distributions normales, avec une variance commune de 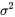 . Tout comme dans la section 5.3, où la version
. Tout comme dans la section 5.3, où la version 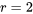 de ce modèle à un facteur (contrairement aux modèles à plusieurs facteurs) a amené des méthodes d’inférence pratiques pour
de ce modèle à un facteur (contrairement aux modèles à plusieurs facteurs) a amené des méthodes d’inférence pratiques pour  , cette version générale permettra d’utiliser de nombreuses méthodes d’inférence pratiques pour les études utilisant
, cette version générale permettra d’utiliser de nombreuses méthodes d’inférence pratiques pour les études utilisant  échantillons. La figure 6.1.2.1 présente plusieurs distributions normales différentes ayant le même écart-type. Essentiellement, elle représente la source des réponses mesurées lorsque l’on applique les méthodes de ce chapitre.
échantillons. La figure 6.1.2.1 présente plusieurs distributions normales différentes ayant le même écart-type. Essentiellement, elle représente la source des réponses mesurées lorsque l’on applique les méthodes de ce chapitre.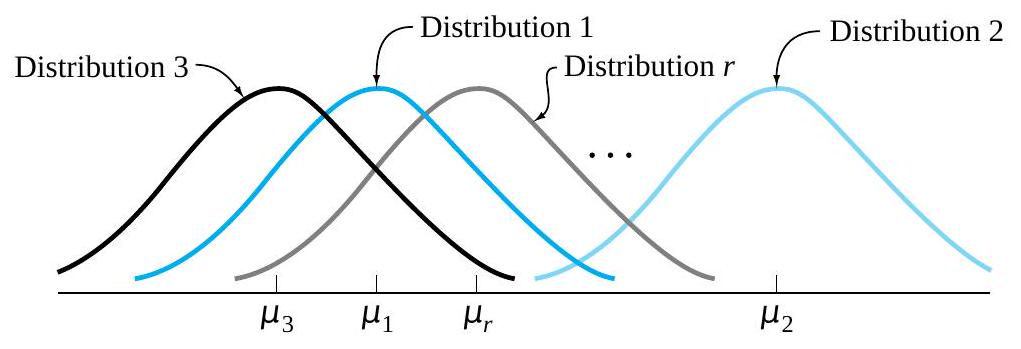
- Figure 6.1.2.1 Distributions normales ayant le même écart-type
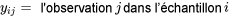
6.1.2.1 Énoncé du modèle à un facteur en symboles
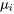 est la
est la  e moyenne sous-jacente et les quantités
e moyenne sous-jacente et les quantités 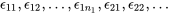 ,
, 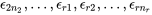 sont des variables aléatoires normales indépendantes de moyenne 0 et de variance
sont des variables aléatoires normales indépendantes de moyenne 0 et de variance 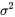 . (Ici, les moyennes
. (Ici, les moyennes 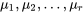 et la variance
et la variance 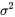 sont typiquement des paramètres inconnus.)
sont typiquement des paramètres inconnus.) se compose de la moyenne sous-jacente correspondante, à laquelle s’ajoute le bruit aléatoire suivant :
se compose de la moyenne sous-jacente correspondante, à laquelle s’ajoute le bruit aléatoire suivant :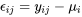
 échantillons, il peut être difficile de savoir comment appliquer les notions de valeurs ajustées et de résidus. Toutefois, il est probable que
échantillons, il peut être difficile de savoir comment appliquer les notions de valeurs ajustées et de résidus. Toutefois, il est probable que
 e échantillon
e échantillonie moyenne d’échantillon
6.1.2.2 Valeurs ajustées pour le modèle à un facteur
 échantillons, le schéma établi indique que les résidus sont les différences entre valeurs observées et moyennes d’échantillon. Par conséquent, avec :
échantillons, le schéma établi indique que les résidus sont les différences entre valeurs observées et moyennes d’échantillon. Par conséquent, avec :
6.1.2.3 Résidus pour modèle à un facteur
6.1.2.4
6.1.2.5
6.1.2.6 Observationréponse déterministe + bruit
valeur ajustée + résidu
1. Les valeurs ajustées 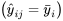 sont censées représenter approximativement la part déterministe de la réponse du système
sont censées représenter approximativement la part déterministe de la réponse du système 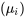 .
.
.
2. Les résidus 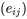 sont donc censés représenter approximativement le bruit correspondant dans la réponse
sont donc censés représenter approximativement le bruit correspondant dans la réponse 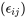 .
.
.
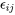 de l’équation 6.1.2.1 sont supposés être des variables aléatoires normales indépendantes et identiquement distribuées (iid)
de l’équation 6.1.2.1 sont supposés être des variables aléatoires normales indépendantes et identiquement distribuées (iid) 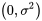 laisse alors supposer que les
laisse alors supposer que les 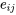 devraient au moins à peu près ressembler à un échantillon aléatoire suivant une distribution normale.
devraient au moins à peu près ressembler à un échantillon aléatoire suivant une distribution normale. échantillons sont souvent très utiles en pratique. Si
échantillons sont souvent très utiles en pratique. Si  est très grand, les contraintes budgétaires concernant le coût total de la collecte de données restreignent souvent la taille
est très grand, les contraintes budgétaires concernant le coût total de la collecte de données restreignent souvent la taille 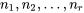 des échantillons à être relativement petite. Cela rend vaine toute étude des hypothèses du modèle de distribution normale de variance unique à l’aide (par exemple) de tracés normaux, échantillon par échantillon. (Évidemment, quand tous les
des échantillons à être relativement petite. Cela rend vaine toute étude des hypothèses du modèle de distribution normale de variance unique à l’aide (par exemple) de tracés normaux, échantillon par échantillon. (Évidemment, quand tous les 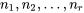 sont de taille décente, l’approche échantillon par échantillon peut être efficace.)
sont de taille décente, l’approche échantillon par échantillon peut être efficace.)Exemple 6.1.2.1 (suite)
Au premier abord, il peut sembler étrange que, dans ce tableau, 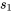 soit plus de trois fois plus grand que
soit plus de trois fois plus grand que 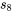 . Mais les échantillons sont si petits (
. Mais les échantillons sont si petits (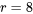 échantillons de taille 3 suivant une distribution normale) que ce n’est pas si inhabituel de voir un rapport de l’ordre de 3,2 entre le plus grand et le plus petit écart-type. À noter que d’après les tables
échantillons de taille 3 suivant une distribution normale) que ce n’est pas si inhabituel de voir un rapport de l’ordre de 3,2 entre le plus grand et le plus petit écart-type. À noter que d’après les tables 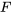 (table A1.5), même si on avait seulement deux écarts-types seulement sont impliqués (plutôt que huit), un rapport de variances de
(table A1.5), même si on avait seulement deux écarts-types seulement sont impliqués (plutôt que huit), un rapport de variances de 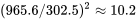 donnerait, pour les échantillons de taille 3, une valeur
donnerait, pour les échantillons de taille 3, une valeur  située entre 0,10 et 0,20 pour le test de l’hypothèse nulle de variances égales, avec une hypothèse alternative bilatérale. Les écarts-types des échantillons du tableau 6.1.2.1 n’indiquent pas foncièrement que le modèle à un facteur n’est pas adapté.
située entre 0,10 et 0,20 pour le test de l’hypothèse nulle de variances égales, avec une hypothèse alternative bilatérale. Les écarts-types des échantillons du tableau 6.1.2.1 n’indiquent pas foncièrement que le modèle à un facteur n’est pas adapté.
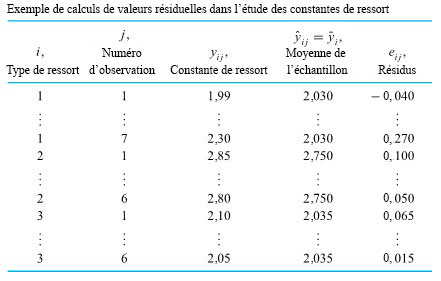
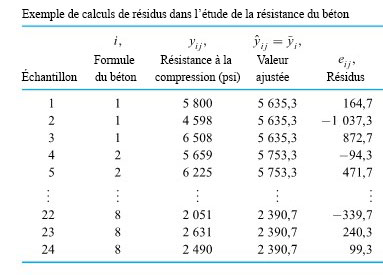
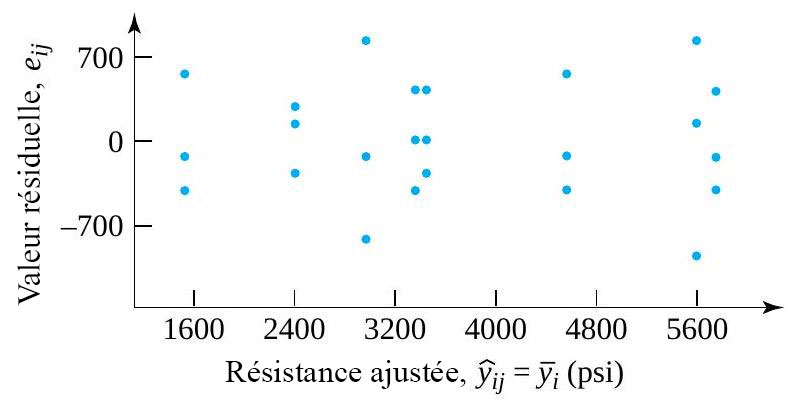
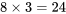 résidus. Le tableau 6.1.2.2 présente certains calculs nécessaires pour obtenir les résidus des données du tableau 6.1.1.1 (en utilisant les valeurs ajustées figurant dans le tableau 6.1.2.1 en tant que moyennes d’échantillons) sont présentés dans. Les figures 6.1.2.2 et 6.1.2.3 représentent respectivement un tracé de résidus en fonction de
résidus. Le tableau 6.1.2.2 présente certains calculs nécessaires pour obtenir les résidus des données du tableau 6.1.1.1 (en utilisant les valeurs ajustées figurant dans le tableau 6.1.2.1 en tant que moyennes d’échantillons) sont présentés dans. Les figures 6.1.2.2 et 6.1.2.3 représentent respectivement un tracé de résidus en fonction de 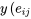 en fonction de
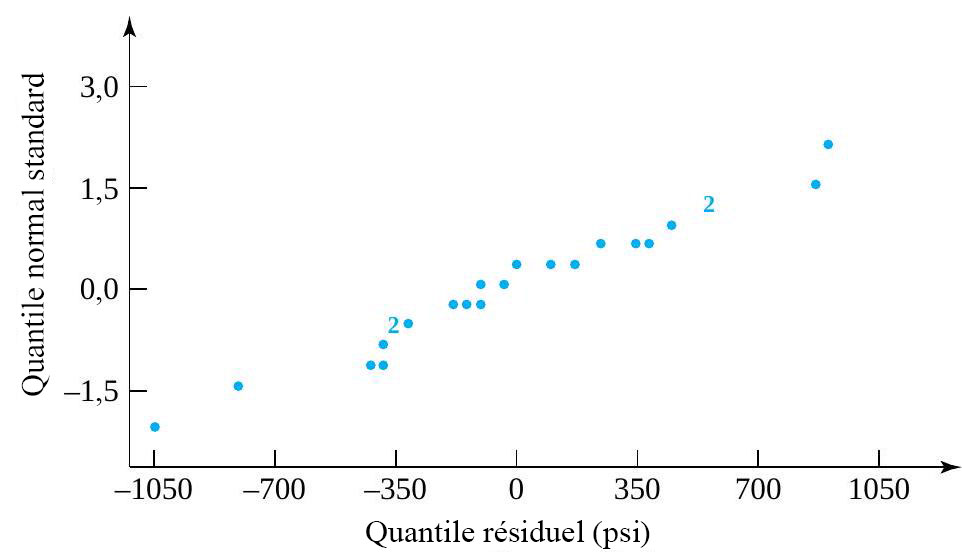
en fonction de 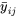 et un tracé normal des 24 résidus.
et un tracé normal des 24 résidus.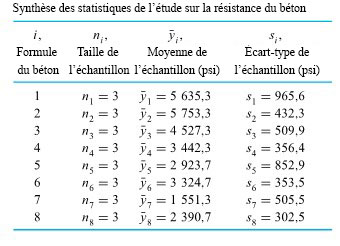
.
.
Exemple 6.1.2.2 Test sur les ressorts (suite)
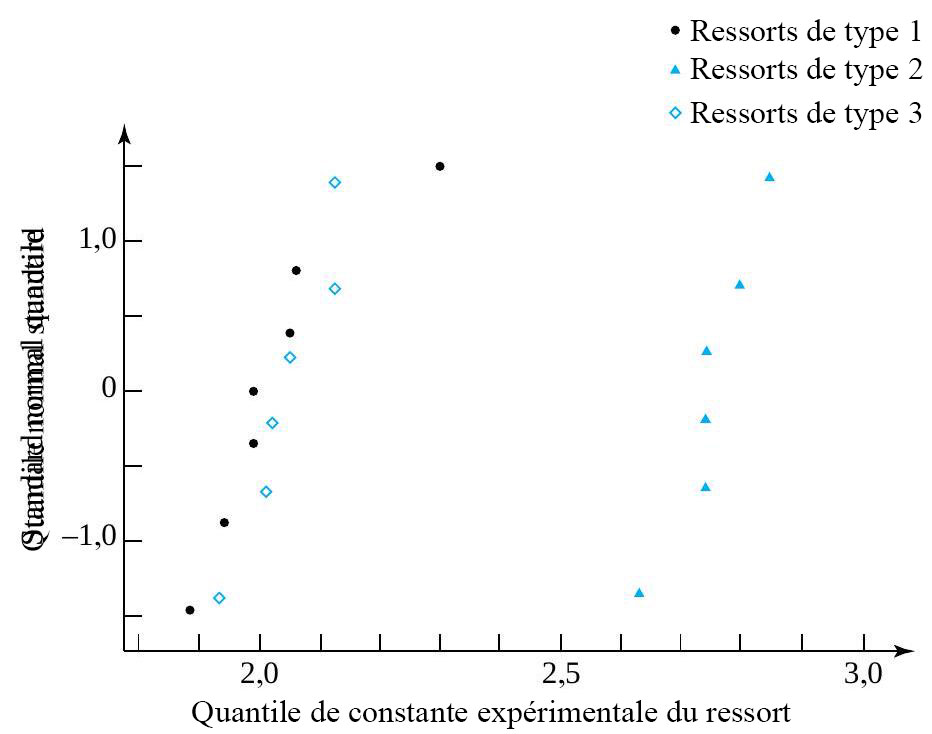
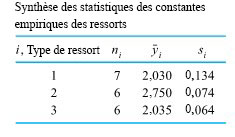
Les données expérimentales sur les ressorts peuvent également être analysées en tenant compte de l’utilisation potentielle du modèle normal à un facteur 6.1.1.1. Les figures 6.1.1.2 et 6.1.1.3 indiquent des variabilités comparables pour les constantes de ressort expérimentales, pour les r = 3 types de ressorts différents. La valeur élevée du ressort de type 1 suscite le doute concernant cette opinion et la description de « distribution normale » des constantes expérimentales de type 1 (en raison de la position de cette valeur aberrante sur le diagramme en boîtes). Le tableau 6.1.2.3 présente des statistiques synthétiques de ces échantillons.
.
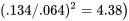 ne suffit pas pour abandonner la description de modèle à un facteur des constantes de ressort. (On constate dans les tables
ne suffit pas pour abandonner la description de modèle à un facteur des constantes de ressort. (On constate dans les tables 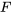 pour
pour 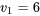 et
et 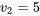 que 4,38 se trouve entre les quantiles 0,9 et 0,95 de la distribution
que 4,38 se trouve entre les quantiles 0,9 et 0,95 de la distribution 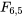 . Par conséquent, même s’il y avait seulement deux échantillons et non trois, un rapport de variance de 4,38 donnerait une valeur
. Par conséquent, même s’il y avait seulement deux échantillons et non trois, un rapport de variance de 4,38 donnerait une valeur  située entre 0,1 et 0,2 pour le test (bilatéral) d’égalité des variances.) Avant de laisser la constante empirique du ressort de type 1 de 2,30 mener à l’abandon du très utile modèle 6.1.2.1, il est judicieux de regarder ce qui se passe d’un peu plus près.
située entre 0,1 et 0,2 pour le test (bilatéral) d’égalité des variances.) Avant de laisser la constante empirique du ressort de type 1 de 2,30 mener à l’abandon du très utile modèle 6.1.2.1, il est judicieux de regarder ce qui se passe d’un peu plus près.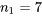 et
et 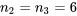 sont suffisamment grandes pour qu’il soit pertinent d’observer les tracés normaux des données constantes des ressorts échantillon par échantillon. La figure 6.1.2.4 présente ces tracés, réalisés sur les mêmes axes. De plus, l’utilisation des valeurs ajustées
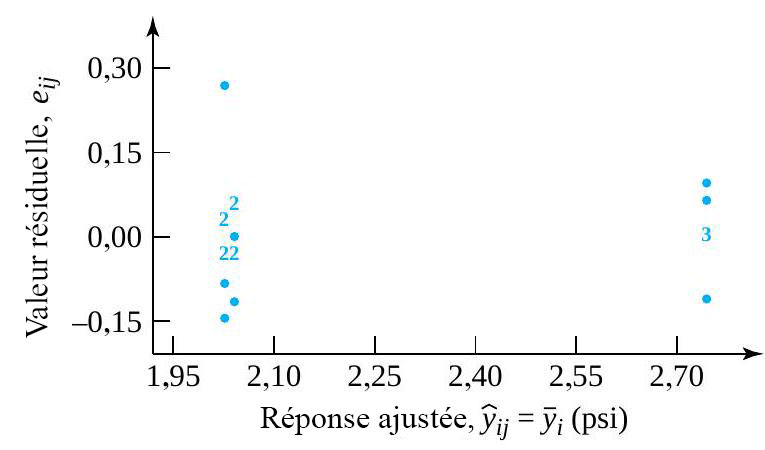
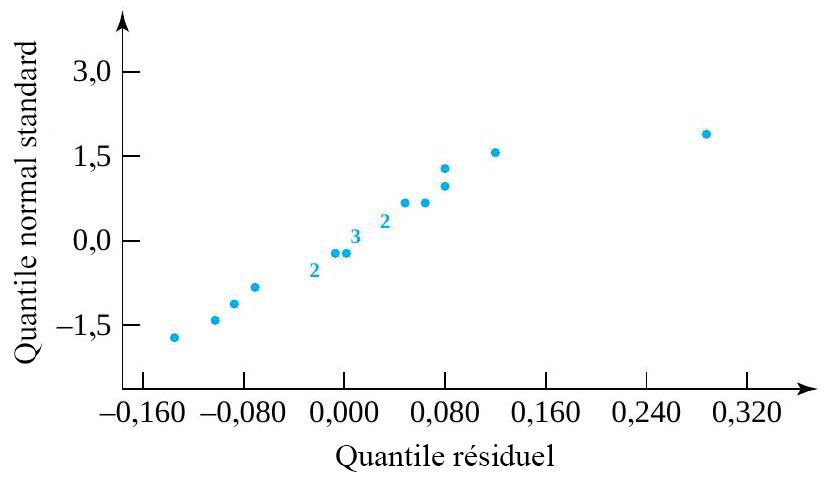
sont suffisamment grandes pour qu’il soit pertinent d’observer les tracés normaux des données constantes des ressorts échantillon par échantillon. La figure 6.1.2.4 présente ces tracés, réalisés sur les mêmes axes. De plus, l’utilisation des valeurs ajustées 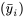 du tableau 6.1.2.3, dont les données originales proviennent du tableau 6.1.1.2, produit 19 résidus, comme l’illustre en partie le tableau 6.1.2.4. Les figures 6.1.2.5 et 6.1.2.6 montrent ensuite respectivement un tracé de résidus en fonction des réponses ajustées, et un tracé normal de l’ensemble des 19 résidus.
du tableau 6.1.2.3, dont les données originales proviennent du tableau 6.1.1.2, produit 19 résidus, comme l’illustre en partie le tableau 6.1.2.4. Les figures 6.1.2.5 et 6.1.2.6 montrent ensuite respectivement un tracé de résidus en fonction des réponses ajustées, et un tracé normal de l’ensemble des 19 résidus.On peut évidemment se limiter à étudier les ressorts de type 2 et 3. Il n’y a rien dans les deuxième et troisième échantillons qui rende le modèle de « distributions normales de même variance » indéfendable pour ces deux types de ressorts. Mais le schéma de variation des ressorts de type 1 semble être clairement différent de celui des ressorts de types 2 et 3, et ce modèle à un facteur n’est donc pas adéquat si l’on tient compte des trois types.
constantes de ressort empiriques