6.1.1 Comparaison graphique de plusieurs échantillons de données de mesure
Exemple 1 Comparaison de la résistance à la compression de huit formules de béton différentes
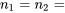
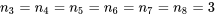 revient à établir un diagramme de dispersion de la résistance à la compression en fonction du numéro de la formule. Ce diagramme est présenté à la figure 6.1.1.1. Ce qui ressort globalement de la figure 6.1.1.1, c’est que les moyennes de résistance à la compression sont nettement différentes d’une formule à l’autre, mais que leurs variabilités sont à peu près comparables.
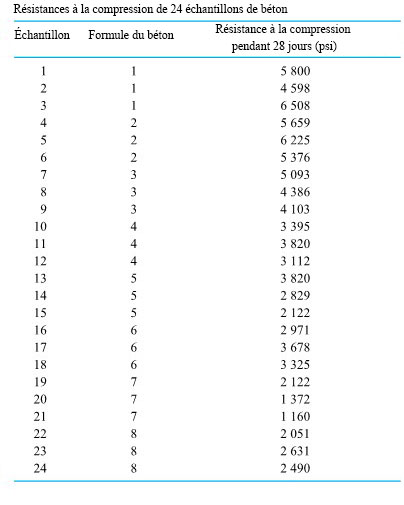
revient à établir un diagramme de dispersion de la résistance à la compression en fonction du numéro de la formule. Ce diagramme est présenté à la figure 6.1.1.1. Ce qui ressort globalement de la figure 6.1.1.1, c’est que les moyennes de résistance à la compression sont nettement différentes d’une formule à l’autre, mais que leurs variabilités sont à peu près comparables.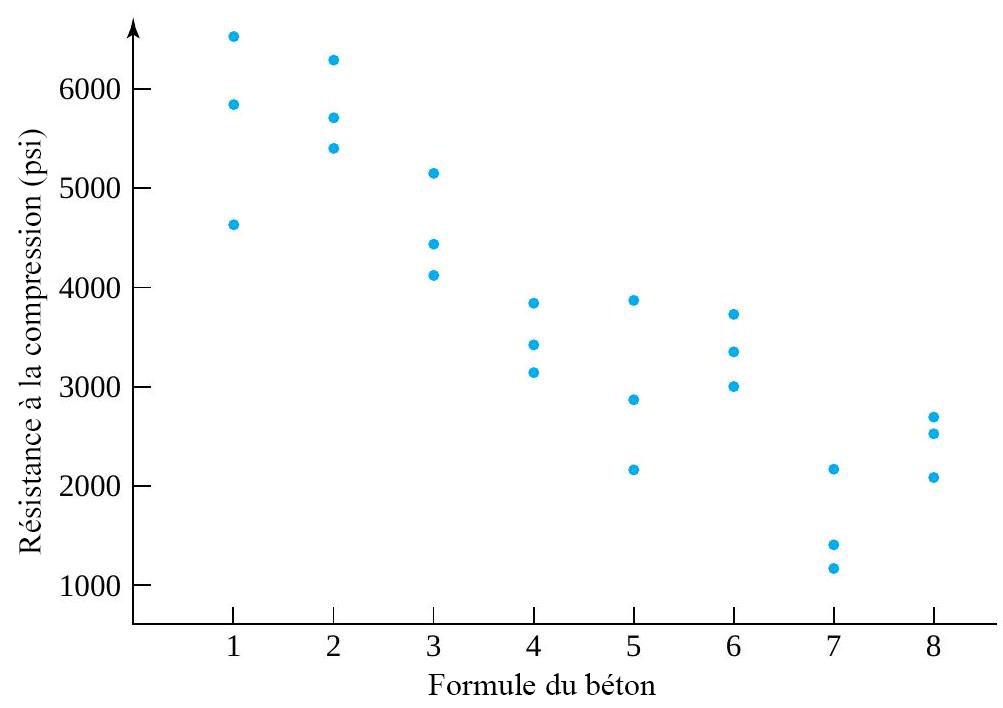
Exemple 6.1.1.2 Comparaison des constantes de ressort empiriques pour trois types de ressorts différents
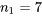 ressorts de type 1 (conception 4 po avec constante de ressort théorique de 1,86),
ressorts de type 1 (conception 4 po avec constante de ressort théorique de 1,86), 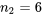 ressorts de type 2 (conception 6 po avec constante de ressort théorique de 2,63) et
ressorts de type 2 (conception 6 po avec constante de ressort théorique de 2,63) et 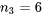 ressorts de type 3 (conception 4 po avec constante de ressort théorique de 2,12), en utilisant une charge de
ressorts de type 3 (conception 4 po avec constante de ressort théorique de 2,12), en utilisant une charge de 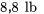 . Les valeurs expérimentales figurent dans le tableau 6.1.1.2.
. Les valeurs expérimentales figurent dans le tableau 6.1.1.2.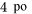 , mais qu’aucune différence entre les deux types de ressorts 4 po n’est évidente. Évidemment, les informations du tableau 6.1.1.2 peuvent également être présentées sous forme de diagramme de dispersion côte à côte, comme dans la figure 6.1.1.3.
, mais qu’aucune différence entre les deux types de ressorts 4 po n’est évidente. Évidemment, les informations du tableau 6.1.1.2 peuvent également être présentées sous forme de diagramme de dispersion côte à côte, comme dans la figure 6.1.1.3.
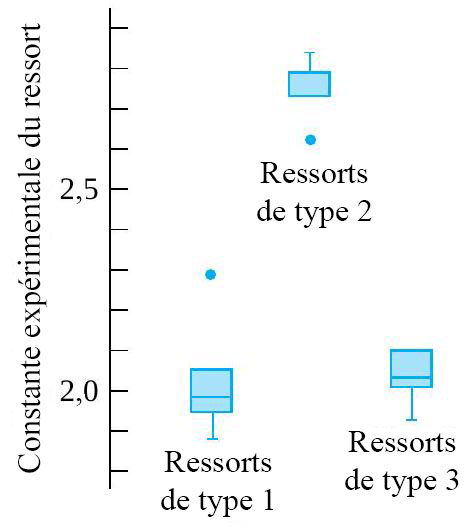
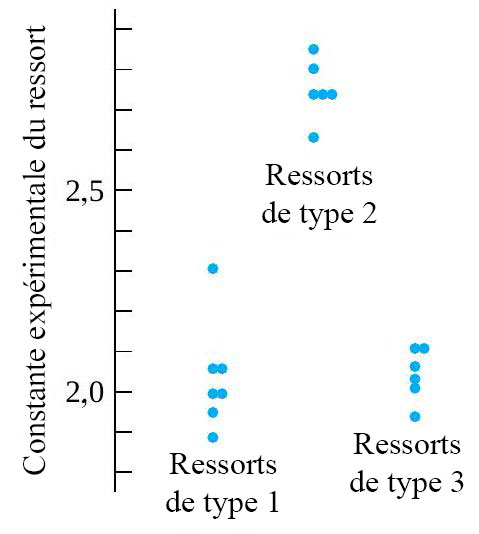
Les méthodes d’inférence statistique formelle ont pour but d’affiner et de quantifier les impressions que l’on peut avoir en réalisant une analyse descriptive de données. Mais en observant intelligemment les graphiques et en appliquant correctement les méthodes d’inférence formelle, il est rare d’obtenir des résultats complètement différents. En effet, les méthodes d’inférence formelle proposées ici pour des études multi-échantillons simples et non structurées sont confirmatoires – dans des cas comme ceux des exemples 1 et 2, ces méthodes ont pour but de confirmer ce qui ressort clairement d’une observation descriptive ou exploratoire des données.
