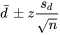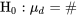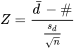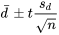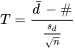5.2.5 Inférence pour moyenne de différences appariées
Les méthodes d’estimation de l’intervalle de confiance et de test d’hypothèse trouvent une application importante dans les données appariées. En ingénierie, il est courant de prendre deux mesures similaires sur le même échantillon d’un objet physique, mais à une heure différente ou à un autre endroit. L’objectif dans ce cas est souvent voir s’il y a un écart constant entre les deux mesures.
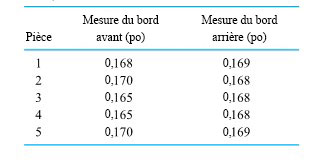
Exemple 5.2.5.1 Comparaison des mesures des bords avant et arrière sur un produit façonné en bois
Drake, Hones et Mulholland ont travaillé avec une entreprise sur le contrôle du fonctionnement d’une fraise à détourer en bout dans une usine fabriquant des produits en bois. Ils ont mesuré une dimension critique d’un certain nombre de pièces d’un type donné lorsqu’elles sortaient de la machine. Les mesures des bords avant et arrière ont été
prises sur chaque pièce. La conception de la pièce en question prévoit que les bords avant et arrière doivent tous deux présenter une valeur cible de 0,172 po. Le tableau 5.2.5.1 indique les mesures de bord avant et de bord arrière prises sur cinq pièces consécutives.
Dans cette situation, le fait que les dimensions des bords avant et arrière correspondent était au moins aussi essentiel à l’assemblage que le fait chaque dimension soit conforme à la valeur nominale de 0,172 po. Il s’agissait donc d’une situation d’appariement de données, dans laquelle l’une des préoccupations était la possibilité d’un écart constant entre les dimensions de bords avant et arrière. (Cet écart pouvait être dû à un mauvais réglage machine ou à une mauvaise utilisation de la machine.)
Dans des situations comme celle de l’exemple 5.2.5.1, une méthode simple pour rechercher un potentiel écart constant entre données appariées consiste à d’abord réduire les deux mesures sur chaque objet physique à leur différence. Les méthodes d’estimation d’intervalle de confiance et de test d’hypothèse étudiées peuvent ensuite être appliquées aux différences. Par conséquent, après avoir réduit les données appariées aux différences d1, d2, …,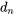 , si n (le nombre de données appariées) est élevé, les bornes de l’intervalle de confiance pour la différence moyenne sous-jacente
, si n (le nombre de données appariées) est élevé, les bornes de l’intervalle de confiance pour la différence moyenne sous-jacente 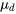 sont
sont
5.2.5.1 Limites de confiance pour
, pour un grand échantillon
où 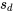 est l’écart-type de l’échantillon d1, d2, …,
est l’écart-type de l’échantillon d1, d2, …,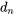 . De même, l’hypothèse nulle
. De même, l’hypothèse nulle
5.2.5.2
peut être testée à l’aide de la variable
5.2.5.3 Variable à tester pour
, grand échantillon
et d’une distribution normale standard de référence.
Si n est petit, pour trouver des méthodes d’inférence formelle, il doit être plausible que les différences suivent une distribution normale. Si tel est le cas, l’intervalle de confiance pour 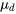 a pour bornes
a pour bornes
5.2.5.4 Limites de confiance pour
suivant une distribution normale
et l’hypothèse nulle (5.2.5.2) peut être testée à l’aide de la variable
5.2.5.5 Variable à tester pour
suivant une distribution normale
et d’une distribution de référence 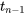 .
.
Suite de l’exemple 5.2.5.2
Pour illustrer cette méthode des différences appariées, testons l’hypothèse nulle  :
: 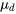 = 0 avec un intervalle de confiance de 95 %, pour tout écart constant entre les dimensions de bords avant et arrière,
= 0 avec un intervalle de confiance de 95 %, pour tout écart constant entre les dimensions de bords avant et arrière, 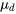 , à l’aide des données du tableau 5.2.5.1
, à l’aide des données du tableau 5.2.5.1
Commençons par réduire les n = 5 observations d’appariement du tableau 5.2.5.1 aux différences
d = dimension du bord avant − dimension du bord arrière
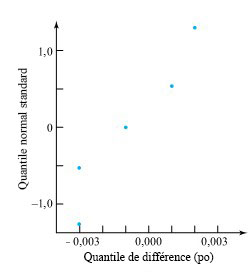
figurant dans le tableau 5.2.5.2. La figure 5.2.5.1 représente un tracé normal des n = 5 différences du tableau 5.2.5.2. Un peu d’expérimentation avec les tracés normaux des échantillons simulés de taille n = 5 suivant une distribution normale suffit à mettre en évidence le fait que le manque de linéarité sur la figure 5.2.5.1 n’est en aucun cas atypique des données normales. Si l’on ajoute à cela le fait que les distributions normales décrivent souvent très bien les dimensions usinées de pièces produites en série, on pourrait en conclure que les méthodes représentées par les expressions 5.2.5.4 et 5.2.5.5 sont de mise dans cet exemple.
Les différences du tableau 5.2.5.2 indiquent 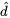 =−0,0008 po et
=−0,0008 po et 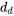 = 0,0023 po. Effectuons un test d’hypothèse en cinq étapes pour voir s’il est plausible d’affirmer que l’écart est constant :
= 0,0023 po. Effectuons un test d’hypothèse en cinq étapes pour voir s’il est plausible d’affirmer que l’écart est constant :
1. H0 : µd = 0.
2. Ha : µd = 0.
(Il n’y a a priori aucune raison d’opter pour une hypothèse alternative unilatérale.)
3. La variable à tester est la suivante :
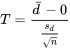
La distribution de référence sera la distribution t avec 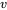 = n − 1 = 4 degrés de liberté. Une grande valeur de |t| permettra d’infirmer
= n − 1 = 4 degrés de liberté. Une grande valeur de |t| permettra d’infirmer  et de confirmer
et de confirmer  .
.
4. L’échantillon donne
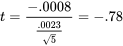
5. Le niveau de signification observé est P [|une variable aléatoire 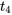 | ≥0,78], ce qui, d’après le tableau A1.2, est supérieur à 2(0,10) = 0,2. Les données ne se montrent pas en faveur d’une différence systématique entre les mesures des bords avant et arrière.
| ≥0,78], ce qui, d’après le tableau A1.2, est supérieur à 2(0,10) = 0,2. Les données ne se montrent pas en faveur d’une différence systématique entre les mesures des bords avant et arrière.
D’après le tableau A1.2 pour le quantile 0,975 de la distribution 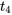 , le multiplicateur à utiliser dans l’expression pour un niveau de confiance à 95 % est t = 2,776. Cela signifie qu’un intervalle de confiance bilatéral à 95 % pour la différence moyenne entre les dimensions des bords avant et arrière a pour bornes
, le multiplicateur à utiliser dans l’expression pour un niveau de confiance à 95 % est t = 2,776. Cela signifie qu’un intervalle de confiance bilatéral à 95 % pour la différence moyenne entre les dimensions des bords avant et arrière a pour bornes
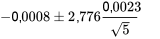
soit :
−0,0008 po ± 0,0029 po
ou encore :
−0,0037 po et 0,0021 po
Cet intervalle de confiance pour 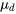 sous-entend (étant donné que 0 fait partie de l’intervalle calculé) que le niveau de confiance observé dans le cadre du test de
sous-entend (étant donné que 0 fait partie de l’intervalle calculé) que le niveau de confiance observé dans le cadre du test de  :
: 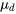 = 0 est supérieur à 0,05 (= 1 − 0,95). En d’autres termes, le calcul de l’IC ci-dessus montre bien que l’imprécision indiquée par le signe plus ou moins de l’expression est suffisamment grande pour concevoir que la différence perçue,
= 0 est supérieur à 0,05 (= 1 − 0,95). En d’autres termes, le calcul de l’IC ci-dessus montre bien que l’imprécision indiquée par le signe plus ou moins de l’expression est suffisamment grande pour concevoir que la différence perçue, 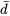 =−0,0008, n’est que le résultat de la variabilité d’échantillonnage.
=−0,0008, n’est que le résultat de la variabilité d’échantillonnage.

Inférence d’un grand échantillon pour 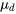
L’Exemple 5.2.5.2 traite un problème sur un petit échantillon. Nous ne présentons pas d’exemple pour n élevé. Un tel exemple ne consisterait qu’à refaire ce qui a déjà été vu. En effet, étant donné que pour un n élevé, la distribution t avec 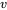 = n − 1 degré de liberté devient essentiellement une distribution normale standard, on pourrait même suivre l’exemple 5.2.5.2 pour n élevé et n’avoir aucun problème de logique. Ce n’est donc plus nécessaire de s’attarder à la méthode des différences appariées.
= n − 1 degré de liberté devient essentiellement une distribution normale standard, on pourrait même suivre l’exemple 5.2.5.2 pour n élevé et n’avoir aucun problème de logique. Ce n’est donc plus nécessaire de s’attarder à la méthode des différences appariées.
Données appariées ou non appariées
Le problème des données appariées (qui contiennent des observations à deux variables sur un seul échantillon) marque un contraste avec le problème précédent où les méthodes s’appliquent à une mesure unique faite sur chaque élément de deux échantillons différents. Dans le cas de l’usinage du bois de l’exemple 5.2.5.2, les données sont appariées puisque les mesures des bords avant et arrière ont été effectuées sur chaque pièce. Si les mesures du bord avant étaient prises sur un groupe de pièces et les mesures du bord arrière sur un autre, il faudrait alors faire une une analyse de deux échantillons (et non une analyse de différences appariées).