5.2.4 Inférence pour les variances de deux échantillons
Inférence pour le rapport de deux variances (basée sur des échantillons indépendants suivant une distribution normale)
Pour passer d’une inférence pour variance unique à une inférence permettant de comparer deux variances, il faut introduire une nouvelle famille de distributions de probabilité : les distributions F de Fisher-Snedecor.
DÉFINITION 5.2.4.1 Distribution F de Fisher-Snedecor
EXPRESSION 5.2.4.1
La distribution F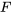 de Fisher-Snedecor avec paramètres de degrés de liberté du numérateur et du dénominateur
de Fisher-Snedecor avec paramètres de degrés de liberté du numérateur et du dénominateur 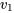 et
et 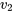 désigne une distribution de probabilité continue ayant pour densité de probabilité
désigne une distribution de probabilité continue ayant pour densité de probabilité
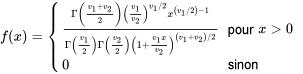 0 \\ 0 & \text { sinon }\end{cases}" title="f(x)= \begin{cases}\frac{\Gamma\left(\frac{v_1+v_2}\right)\left(\frac{v_1}{v_2}\right)^{v_1 / 2} x^{\left(v_1 / 2\right)-1}}{\Gamma\left(\frac{v_1}\right) \Gamma\left(\frac{v_2}\right)\left(1+\frac{v_1 x}{v_2}\right)^{\left(v_1+v_2\right) / 2}} & \text { pour } x>0 \\ 0 & \text { sinon }\end{cases}" class="latex mathjax">
0 \\ 0 & \text { sinon }\end{cases}" title="f(x)= \begin{cases}\frac{\Gamma\left(\frac{v_1+v_2}\right)\left(\frac{v_1}{v_2}\right)^{v_1 / 2} x^{\left(v_1 / 2\right)-1}}{\Gamma\left(\frac{v_1}\right) \Gamma\left(\frac{v_2}\right)\left(1+\frac{v_1 x}{v_2}\right)^{\left(v_1+v_2\right) / 2}} & \text { pour } x>0 \\ 0 & \text { sinon }\end{cases}" class="latex mathjax">
Si une variable aléatoire présente une densité de probabilité donnée par la formule (5.2.4.1), on dit qu’elle a une distribution 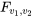 .
.
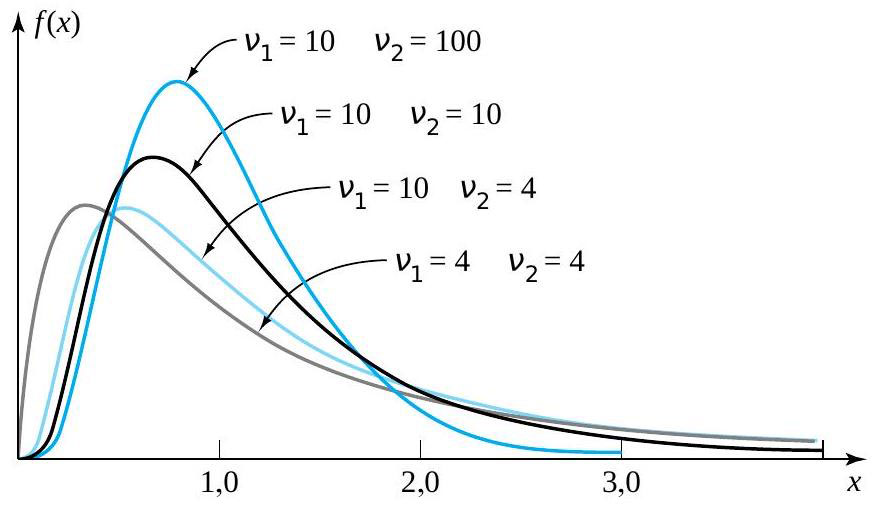
Comme le montre la Figure 5.2.4.1, les distributions F de Fisher-Snedecor sont des distributions à forte asymétrie droite, dont le maximum se situe à un argument légèrement inférieur à 1. Globalement, plus les valeurs 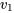 et
et 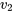 sont basses, plus la distribution F de Fisher-Snedecor concernée est asymétrique et étalée.
sont basses, plus la distribution F de Fisher-Snedecor concernée est asymétrique et étalée.
Utilisation des tables de distribution F (de Fisher-Snedecor), Tableau A1.5Utiliser directement la formule (5.2.4.1) pour trouver des probabilités pour la distribution 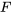 nécessite d’employer des méthodes d’intégration numérique. Pour appliquer la distribution
nécessite d’employer des méthodes d’intégration numérique. Pour appliquer la distribution 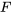 en inférence statistique, on utilise plutôt soit un logiciel de statistiques, soit des tables très abrégées de quantiles de distribution
en inférence statistique, on utilise plutôt soit un logiciel de statistiques, soit des tables très abrégées de quantiles de distribution 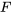 . Les tableaux A1.5 en annexe sont des tables de quantiles
. Les tableaux A1.5 en annexe sont des tables de quantiles 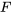 . Ils présentent, pour une valeur de
. Ils présentent, pour une valeur de  donnée, les quantiles
donnée, les quantiles  de la distribution
de la distribution 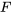 pour différentes combinaisons de
pour différentes combinaisons de 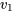 (le degré de liberté du numérateur) et
(le degré de liberté du numérateur) et 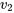 (le degré de liberté du dénominateur). Les valeurs de
(le degré de liberté du dénominateur). Les valeurs de 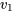 sont données dans l’en-tête de la table, et les valeurs de
sont données dans l’en-tête de la table, et les valeurs de 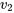 , dans la colonne de gauche.
, dans la colonne de gauche.
Les tableaux A1.5 ne donnent que les quantiles  pour
pour  supérieur à 0,5, mais les quantiles de distribution
supérieur à 0,5, mais les quantiles de distribution 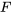 pour
pour  inférieur à 0,5 sont souvent également utiles. Plutôt que de créer des tables pour ces valeurs, la pratique la plus courante est d’utiliser une astuce de calcul. En effet, le rapport entre les quantiles
inférieur à 0,5 sont souvent également utiles. Plutôt que de créer des tables pour ces valeurs, la pratique la plus courante est d’utiliser une astuce de calcul. En effet, le rapport entre les quantiles 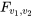 et
et 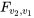 permet de déterminer les quantiles pour de faibles
permet de déterminer les quantiles pour de faibles  . Soit
. Soit 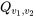 la fonction quantile
la fonction quantile 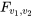 et
et 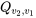 la fonction quantile pour la distribution
la fonction quantile pour la distribution 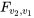 , alors
, alors
EXPRESSION 5.2.4.2 Rapport entre quantiles 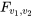 et
et 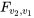
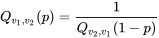
L’encadré (5.2.4.2) indique qu’il est possible d’obtenir un point de pourcentage de distribution inférieur en prenant l’inverse d’un point de pourcentage de distribution supérieur correspondant, en inversant les degrés de liberté.
Exemple 5.2.4.1 Utilisation des tables de quantiles de distribution
Supposons que 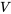 soit une variable aléatoire
soit une variable aléatoire 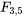 . Cherchons les quantiles .95 et .01 de la distribution de
. Cherchons les quantiles .95 et .01 de la distribution de 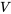 , puis regardons ce que le tableau A1.5 révèle sur
, puis regardons ce que le tableau A1.5 révèle sur 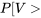 " title="P[V>" class="latex mathjax"> 4,0] et <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/109e3ebc4e9893167fd000040c2f0f7b.png" alt="P[V<0,3]" title="P[V.
" title="P[V>" class="latex mathjax"> 4,0] et <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/109e3ebc4e9893167fd000040c2f0f7b.png" alt="P[V<0,3]" title="P[V.
En consultant directement la table des quantiles pour 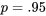 , colonne
, colonne 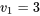 , ligne
, ligne 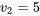 , on trouve dans un premier temps le nombre 5,41. Autrement dit,
, on trouve dans un premier temps le nombre 5,41. Autrement dit, 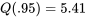 , ce qui équivaut à dire que <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e87e037cb2d9dc42f354bdabcc0770e6.png" alt="P[V<5,41]=0,95" title="P[V.
, ce qui équivaut à dire que <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e87e037cb2d9dc42f354bdabcc0770e6.png" alt="P[V<5,41]=0,95" title="P[V.
Pour trouver le quantile 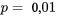 de la distribution
de la distribution 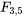 , il faut utiliser l’expression (5.2.4.2), soit :
, il faut utiliser l’expression (5.2.4.2), soit :
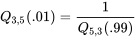
de sorte qu’en utilisant la colonne 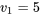 et la ligne
et la ligne 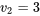 de la table de quantiles
de la table de quantiles 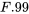 , on obtient :
, on obtient :
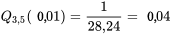
En considérant ensuite que 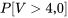 4,0]" title="P[V>4,0]" class="latex mathjax">, on constate (en utilisant la colonne [/latex]v_{1}=3[/latex] et la ligne
4,0]" title="P[V>4,0]" class="latex mathjax">, on constate (en utilisant la colonne [/latex]v_{1}=3[/latex] et la ligne 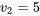 du tableau A1.5) que 4,0 se situe entre les quantiles 0,90 et 0,95 de la distribution
du tableau A1.5) que 4,0 se situe entre les quantiles 0,90 et 0,95 de la distribution 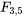 . C’est à dire que
. C’est à dire que
0,90<P[V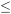 4.0]<0,95
4.0]<0,95
de sorte que
0,05<P[V>4,0]<0,10
Enfin, si l’on considère que <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/109e3ebc4e9893167fd000040c2f0f7b.png" alt="P[V<0,3]" title="P[V, notons qu’aucune des entrées des tableaux A1.5 n’est inférieure à 1,00. Ainsi, pour placer la valeur 3 dans la distribution 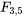 , il faut localiser sa réciproque, 3,33 (
, il faut localiser sa réciproque, 3,33 ( 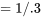 ), dans la distribution
), dans la distribution 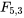 , puis utiliser l’expression (5.2.4.2). En utilisant les colonnes
, puis utiliser l’expression (5.2.4.2). En utilisant les colonnes 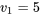 et les lignes
et les lignes 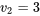 des tableaux A1.5, on constate alors que 3,33 se situe entre les quantiles 0,75 et 0,90 de la distribution
des tableaux A1.5, on constate alors que 3,33 se situe entre les quantiles 0,75 et 0,90 de la distribution 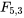 . Donc d’après l’expression (5.2.4.2), 0,3 se situe entre les quantiles 0,1 et 0,25 de la distribution
. Donc d’après l’expression (5.2.4.2), 0,3 se situe entre les quantiles 0,1 et 0,25 de la distribution 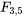 , et
, et
0,10<P[V<0,3]<0,25
Cet effort pour déterminer les faibles quantiles de distribution F est une conséquence des normes de création des tables, et non une particularité propres aux distributions F. Pour faciliter les choses et trouver les quantiles F plus simplement, il est notamment possible d’utiliser un logiciel de statistiques standard ou une calculatrice scientifique.
La distribution F est utilisée ici, car un fait de probabilité lie le comportement des rapports des variances d’échantillons indépendants (basés sur des échantillons suivant une distribution normale) aux variances 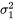 et
et 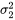 des distributions sous-jacentes. Autrement dit, lorsque
des distributions sous-jacentes. Autrement dit, lorsque 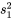 et <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/4271702ef47127321ec8a369ddc787e9.png" alt="s_^[latex][/latex] proviennent d’échantillons indépendants suivant une distribution normale, la variable
et <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/4271702ef47127321ec8a369ddc787e9.png" alt="s_^[latex][/latex] proviennent d’échantillons indépendants suivant une distribution normale, la variable
5.2.4.3 [latex][/latex]F=\frac{s_^}{\sigma_^} \cdot \frac{\sigma_^}{s_^}" title="s_^[latex][/latex] proviennent d’échantillons indépendants suivant une distribution normale, la variable
5.2.4.3 [latex][/latex]F=\frac{s_^}{\sigma_^} \cdot \frac{\sigma_^}{s_^}" class="latex mathjax">
suit une distribution
. (
a
degrés de liberté associés et figure dans le numérateur de cette expression, tandis que
a
degrés de liberté associés et figure dans le dénominateur, motivant le langage introduit à la définition 5.2.4.1)
C’est exactement dont nous avons besoin pour produire des méthodes d’inférence formelles pour le rapport
. Il est par exemple possible de choisir L et U, les bons quantiles F, de sorte que la probabilité que la variable (5.2.4.3) se situe entre L et U corresponde au niveau de confiance souhaité. (L et U sont typiquement choisis de manière à « répartir le manque de confiance » entre les queues
supérieure et inférieure.) Mais
L<
<U
équivaut algébriquement à
<img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/3832fa902041ddfb0c0504d802139bb0.png" alt="\frac{U} \cdot \frac{s_^}{s_^}<\frac{\sigma_^}{\sigma_^}<\frac{L} \cdot \frac{s_^}{s_^}" title="\frac{U} \cdot \frac{s_^}{s_^}<\frac{\sigma_^}{\sigma_^}Autrement dit, lorsqu’un mécanisme de génération de données peut être considéré comme fondamentalement équivalent à un échantillonnage aléatoire indépendant suivant deux distributions normales, l’intervalle de confiance bilatéral poura pour bornes
5.2.4.4 Limites de confiance de distribution normale pour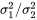 où L et U (quantiles
où L et U (quantiles) sont tels que la probabilité
assignée à l’intervalle (L, U) correspond au niveau de confiance souhaité.
De plus, il y a une méthode de test d’hypothèse évidente pour. Sous réserve des limites de modélisation nécessaires pour que la méthode d’intervalle de confiance s’applique,
5.2.4.5peut être testée à l’aide de la statistique5.2.4.6 Variable à tester suivant une distribution normale pouret d’une distribution de référence. (Le choix de
dans les encadrés (5.2.4.5) et (5.2.4.6) correspond à une hypothèse nulle où les variances sont égales. C’est le seul choix communément utilisé en pratique.)
Valeurs P de test
Les valeurspour les hypothèses alternatives unilatérales
< # et
\#" title="\mathrm{H}_{\mathrm{a}}: \sigma_1^2 / \sigma_2^2>\#" class="latex mathjax"> sont (respectivement) les queues de distribution
gauche et droite au-delà des valeurs observées de la variable à tester. Pour les hypothèses bilatérales alternatives
, la convention standard est de reporter deux fois la probabilité
à droite de la fonction étudiée si
1" title="f>1" class="latex mathjax">, et de reporter deux fois la probabilité
à gauche de la fonction
étudiée si
<1.
Exemple 5.2.4.2 Comparaison de l’uniformité des mesures d’indice de dureté de deux types d’acier
Condon, Smith et Woodford ont mené des essais de dureté sur des échantillons d’acier au carbone à. Une partie de leurs données figurent dans le tableau 5.2.4.1, où sont représentées les mesures de dureté de Rockwell pour dix échantillons provenant d’un lot d’acier à traitement thermique et cinq échantillons provenant d’un lot d’acier laminé à froid.
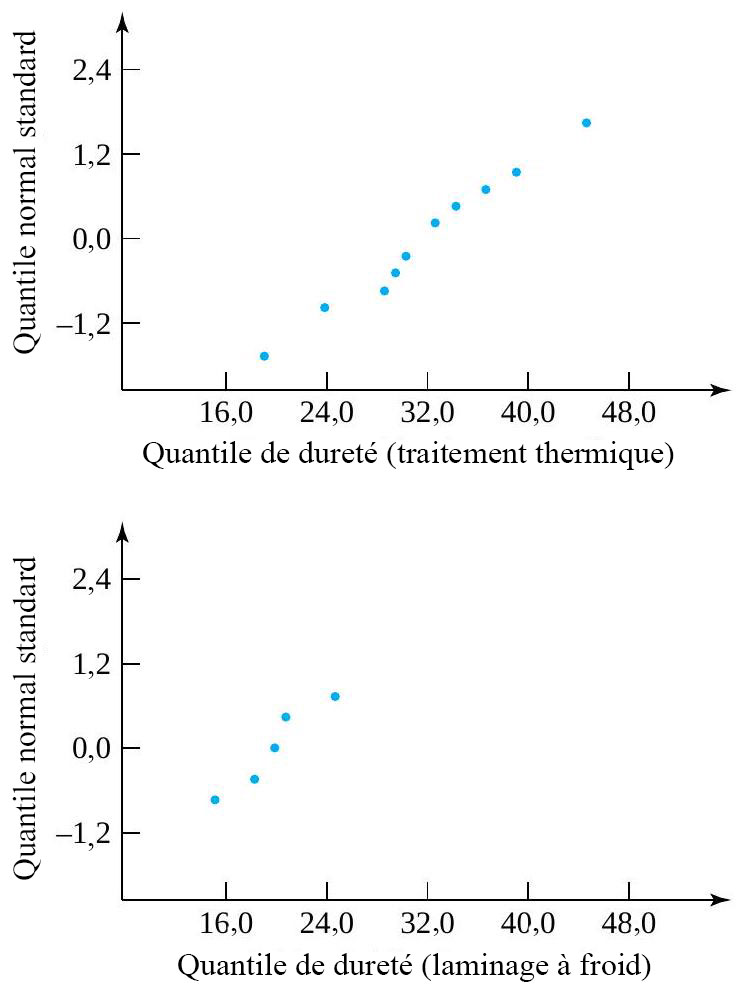
Comparons l’uniformité des mesures de dureté pour ces deux types d’acier (plutôt que la dureté moyenne, comme on l’a fait au chapitre 5.2.3). La figure 5.2.4.2 présente les diagrammes de dispersion de chaque échantillon et suggère que la variabilité associée aux échantillons d’acier à traitement thermique est plus élevée que celle associée aux échantillons d’acier laminé à froid. Les deux tracés normaux de la Figure 5.2.4.3 ne démontrent aucun problème clair avec l’hypothèse que les variables suivent une distribution normale.
Tableau 5.2.4.1 Mesures de dureté de Rockwell pour échantillons de deux types d’acier
Traitement thermique
Laminage à froid
Figure 5.2.4.2 Diagrammes de dispersion présentant la dureté de l’acier à traitement thermique et de l’acier laminé à froid
Figure 5.2..4.3 Tracés de dureté normaux pour acier à traitement thermique et acier laminé à froidChoisissons arbitrairement ensuite d’appeler condition numéro 1 le traitement thermique et condition numéro 2 le laminage à froid, on aet
; un test d’hypothèse d’égalité des variances en cinq étapes reposant sur la variable (5.2.4.6) se présente comme suit :
1.
2.
(Si une raison matérielle justifie le choix d’une autre hypothèse unilatérale, les auteurs n’en ont pas connaissance.)
3. La variable à tester est la suivante :
.La distribution de référence est la distribution, et
sera infirmée si la valeur observée de f est soit grande, soit petite.
.4. Les échantillons donnent..5. Comme f est supérieure à 1, pour l’alternative bilatérale, la valeur p est la suivante :..D’après les tableaux A1.5, 4,6 se situe entre les quantiles 0,9 et 0,95 de la distribution, donc le niveau de signification étudié se situe entre 0,1 et 0,2. Il semble donc peu probable (bien que pas impossible) que le traitement thermique et le laminage à froid aient des variabilités égales.
.Afin de préciser la taille relative des variabilités, les racines carrées des valeurs dans l’expression 5.2.4.6 peuvent être utilisées pour obtenir un intervalle de confiance bilatéral de 90 % pour le rapport. Comme le quantile 0,95 de la distribution
vaut 6,0 et que le quantile 0,95 de la distribution
vaut 3,63, le quantile .05 de la distribution
est
. Ainsi, l’intervalle de confiance de 90 % pour le rapport d’écarts-types
a pour bornes
..En faisant le calcul, on obtient :.0,87 et 4,07.Le fait que l’intervalle (0,87, 4,07) couvre des valeurs à la fois inférieures et supérieures à 1 indique que les données ne permettent pas de déterminer précisément laquelle des deux variabilités est la plus élevée.L’une des plus importantes applications en ingénierie des méthodes d’inférence représentées par ces expressions, c’est de pouvoir comparer la précision intrinsèque de diverses pièces d’équipement ou de diverses méthodes de fonctionnement d’une pièce d’équipement donnée.Exemple 4.2.4.3 Comparaison de l’uniformité de fonctionnement de deux massicots
Abassi, Afinson, Shezad et Yeo ont travaillé avec une entreprise de découpe de feuilles de papier à partir de rouleaux. L’uniformité de la longueur des feuilles est importante, car meilleure elle est, plus la longueur moyenne des feuilles peut se rapprocher de la valeur nominale sans générer de sous-dimensionnement, réduisant ainsi le gaspillage pour l’entreprise.
Les étudiant.e.s ont comparé l’uniformité des feuilles coupées à l’aide de deux massicots, l’un étant muni d’un frein manuel, et l’autre d’un frein automatique. Cette comparaison se base sur les écarts-types estimés de longueur de feuille coupée par les deux machines – précisément le genre de données qu’on utilise pour
poser le cadre des inférences formelles de cette section. Les étudiant.e.s ont estimé que/
était de l’ordre de 1,5. Selon leurs calculs, il faudrait tout au plus deux ans pour que l’entreprise récupère les coûts requis pour équiper tous les massicots de freins automatiques.
Avertissement concernant les inférences pour variance
Si l’on veut faire preuve de rigueur, les méthodes de cette section ne s’appliquent qu’aux distributions normales. Il est pertinent de se demander à quel point cette condition est essentielle pour qu’on puisse recourir à ces méthodes d’inférence pour une ou deux variances. À la fin du module 5.2.3, nous avions mentionné que les méthodes pour les moyennes tiennent relativement la route en cas de violation modérée des hypothèses du module. Malheureusement, ce n’est pas le cas des méthodes pour les variances présentées ici.
Pour ces méthodes, si les données ne suivent pas une distribution normale, le niveau de confiance nominal et les valeurs p peuvent facilement induire en erreur. Par conséquent, il est essentiel d’examiner minutieusement les données (comme on l’a fait avec les tracés normaux dans les exemples) pour justifier l’utilisation des méthodes de la présente section. Les tracés normaux n’étant typiquement pas très révélateurs à moins que l’échantillon concerné ne soit de taille moyenne ou grande, les inférences formelles pour variances seront plus fiables si les échantillons (d’apparence normale) sont de taille moyenne ou grande.
L’importance de la distribution normale en matière de fonctionnement prévisible des méthodes de cette section n’est pas la seule raison de préférer des échantillons de grande taille pour les inférences pour variances. L’expérience révèle rapidement que même s’ils suivent une loi normale, les petits échantillons sont souvent inadéquats pour répondre aux questions pratiques sur les variances. Les intervalles de confiance F pour les variances et le rapport des variances de petits échantillons peuvent être tellement grands qu’ils n’ont guère d’utilité pratique. De fait, il faut généralement utiliser de grands échantillons pour résoudre les problèmes de variances dans le monde réel. Cet avis n’est pas une admission de défaut de ces méthodes; il s’agit simplement d’une mise en garde et d’une explication sur le fait que pour être véritablement parlantes, les variances nécessitent plus de données que les moyennes (par exemple).

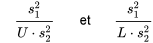
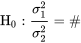
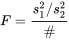
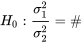


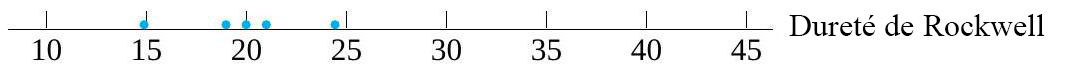
![]\mathrm{H}_{0}: \frac{\sigma_^}{\sigma_^}=1 ]\mathrm{H}_{0}: \frac{\sigma_^}{\sigma_^}=1](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/48b5d327892768d2dc3bab2f2eb7f65a.png)
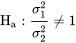
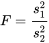
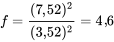
![2 P\left[\text { une variable aléatoire } F_{9,4} \text { } \geq 4,6\right] 2 P\left[\text { une variable aléatoire } F_{9,4} \text { } \geq 4,6\right]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/0536231e06063adb1b166b4daff68e4f.png)
