5.2.2 Comparaisons de deux moyennes sur un grand échantillon (basées sur des échantillons indépendants)
Tournons-nous maintenant vers les méthodes pouvant être utilisées pour comparer deux moyennes tirées de deux échantillons distincts « sans lien de parenté », en commençant par les méthodes pour les grands échantillons.
Exemple 5.2.2.1 Comparaison des propriétés d’empilement de morceaux moulés et concassés d’un solide
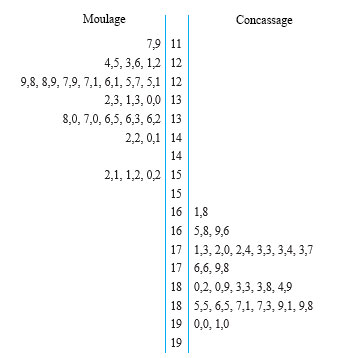
Une entreprise voulait trouver une géométrie fonctionnelle pour les pièces moulées d’un solide. Une des comparaisons effectuées portait sur le poids de pièces versées dans un contenant donné, en s’attardant sur la différence entre les pièces moulées selon une certaine géométrie et es pièces irrégulières obtenues par concassage. Une série de 24 tentatives de remplissage de morceaux moulés et concassés du solide a permis d’obtenir les données (en grammes) présentées à la figure 5.2.2.1 sous de diagrammes à tiges et à feuilles juxtaposés.
On remarque que, bien que la figure présente le même nombre de masses de pièces moulées que de masses de pièces concassés, les deux types d’échantillons sont nettement différents. Cette situation ne se compare en rien à celles de différence appariée traitées dans un autre chapitre, ce qui suggère d’utiliser une autre méthode d’inférence statistique.
Dans des situations comme celle de l’exemple 5.2.2.1, il est utile de noter les paramètres et les statistiques par des indices – par exemple, en prenant 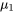 et
et 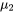 pour représenter les moyennes distributionnelles sous-jacentes correspondant aux première et deuxième conditions et
pour représenter les moyennes distributionnelles sous-jacentes correspondant aux première et deuxième conditions et 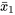 et
et 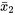 pour représenter les moyennes de l’échantillon correspondantes. Or, si les deux mécanismes de génération de données correspondent essentiellement et conceptuellement à un échantillonnage avec remplacement à partir de deux distributions, la partie 4 indique que
pour représenter les moyennes de l’échantillon correspondantes. Or, si les deux mécanismes de génération de données correspondent essentiellement et conceptuellement à un échantillonnage avec remplacement à partir de deux distributions, la partie 4 indique que 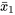 a une moyenne
a une moyenne 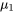 et une variance
et une variance 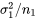 , et que
, et que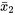 a une moyenne
a une moyenne 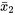 et une variance
et une variance 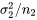 . La différence entre les moyennes des échantillons
. La différence entre les moyennes des échantillons 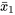 −
− 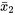 est une statistique naturelle à utiliser pour comparer
est une statistique naturelle à utiliser pour comparer 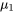 et
et 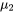 . Toujours selon la partie 4, s’il paraît raisonnable de percevoir les deux échantillons comme étant choisis séparément ou indépendants, cette variable aléatoire a l’espérance mathématique :
. Toujours selon la partie 4, s’il paraît raisonnable de percevoir les deux échantillons comme étant choisis séparément ou indépendants, cette variable aléatoire a l’espérance mathématique :
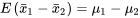
et la variance
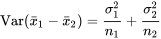
Si, en outre,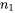 et
et 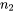 sont grands (de sorte que
sont grands (de sorte que 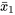 et
et 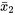 sont toutes deux approximativement normales),
sont toutes deux approximativement normales), 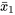 –
– 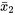 est approximativement normale. Ainsi,
est approximativement normale. Ainsi,
EXPRESSION 5.2.2.1
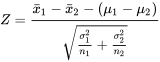
suit une distribution de probabilité approximativement normale.
Comme la variable 5.2.2.1 est approximativement normale réduite, on peut obtenir un intervalle de confiance et à des méthodes de test d’hypothèse pour 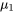 −
− 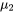 en utilisant une logique exactement parallèle à celle des parties « σ connu » du module 5.1. Mais dans la pratique, il s’avère beaucoup plus utile de commencer par une expression sans
en utilisant une logique exactement parallèle à celle des parties « σ connu » du module 5.1. Mais dans la pratique, il s’avère beaucoup plus utile de commencer par une expression sans 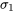 ni
ni 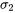 . Heureusement, si
. Heureusement, si 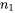 et
et 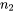 sont grands, non seulement la variable 5.2.2.1 est approximativement normale réduite, mais il en va de même pour
sont grands, non seulement la variable 5.2.2.1 est approximativement normale réduite, mais il en va de même pour
EXPRESSION 5.2.2.2
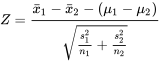
Ainsi, la logique standard du module 5.1 démontre que l’intervalle de confiance bilatéral de la différence des moyennes 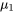 −
− 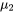 , basé sur deux grands échantillons indépendants, a les bornes suivantes :
, basé sur deux grands échantillons indépendants, a les bornes suivantes :
EXPRESSION 5.2.2.3 Bornes de confiance pour 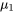 −
− 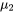 (n = grand)
(n = grand)
[latex]\bar{x}_1-\bar{x}_2 \pm z \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}[/latex]
où z est choisie de sorte que la probabilité que la distribution normale standard attribue à l’intervalle entre -z et z correspond à la confiance souhaitée. Et la logique exposée au module 5.2 démontre que, dans les mêmes conditions,

peut être testée à l’aide de la statistique
EXPRESSION 5.2.2.4 Statistique de test pour 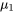 −
− 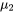 (n = grand)
(n = grand)
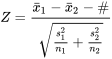
et d’une distribution normale réduite de référence.
Exemple 5.2.2.2 suite.
Dans le problème du moulage, on s’attendait a priori à ce que les pièces concassées s’empilent mieux que les pièces moulées (qui, autrement, conviennent mieux). Mesurons la signification statistique de la différence entre les poids moyens et établissons un intervalle de confiance unilatéral à 95 % pour cette différence (ce qui revient à affirmer que le
de la différence de poids moyen du concassé moins le poids moyen du moulé équivaut au moins à un certain nombre).
La taille des échantillons (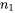 =
= 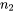 = 24) se situe à la limite de ce que l’on peut qualifier de grand. Il aurait été préférable d’avoir quelques observations de plus pour chaque type, mais faute de quoi, on utilisera la méthode des expressions 5.2.2.3 et 5.2.2.4, tout en faisant preuve de réserve à l’égard des résultats si ces derniers conduisaient à une décision « serrée » au sens de l’ingénierie ou des affaires.
= 24) se situe à la limite de ce que l’on peut qualifier de grand. Il aurait été préférable d’avoir quelques observations de plus pour chaque type, mais faute de quoi, on utilisera la méthode des expressions 5.2.2.3 et 5.2.2.4, tout en faisant preuve de réserve à l’égard des résultats si ces derniers conduisaient à une décision « serrée » au sens de l’ingénierie ou des affaires.
En étiquetant arbitrairement la condition 1 « concassé » et la condition 2 « moulé » et en calculant à partir des données de la figure 5.2.2.2 que alt\bar{x}_1alttitle\bar{x}_1title = 179,55 g, 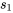 = 8,34 g,
= 8,34 g, 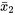 132,97 g et
132,97 g et 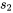 = 9,31 g, le modèle de test d’hypothèse en cinq étapes conduit au récapitulatif suivant :
= 9,31 g, le modèle de test d’hypothèse en cinq étapes conduit au récapitulatif suivant :
1. 
2.  0" title="\mathrm{H}_{\mathrm{a}}: \mu_1-\mu_2>0" class="latex mathjax">
0" title="\mathrm{H}_{\mathrm{a}}: \mu_1-\mu_2>0" class="latex mathjax">
(L’hypothèse de recherche retenue ici est que la moyenne du concassé surpasse la moyenne du moulé,
de sorte que la différence, prise dans cet ordre, est positive.)
3.La statistique de test est la suivante :
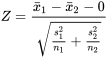
La distribution de référence est normale réduite, et de grandes valeurs |z| observées constitueront une preuve contre  et en faveur de
et en faveur de  .
.
4. Les échantillons donnent
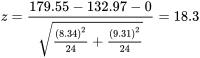
5. Le seuil de signification observé correspond à P[une variable normale réduite ≥ 18,3] ≈ 0. Les données indiquent de manière irréfutable que 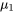
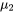 0" title="\mu_2> 0" class="latex mathjax"> : le poids moyen d’empilement des pièces concassées surpasse celui des pièces moulées.
0" title="\mu_2> 0" class="latex mathjax"> : le poids moyen d’empilement des pièces concassées surpasse celui des pièces moulées.
En ce qui à trait à l’intervalle de confiance unilatéral pour 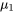 −
− 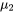 , il convient de noter que seule la borne inférieure donnée dans l’équation 5.2.2.3 sera utilisée. Par conséquent, z = 1,645 conviendra. Autrement dit, avec une confiance de 95 %, on peut conclure que la différence entre les moyennes (concassé moins moulé) surpasse
, il convient de noter que seule la borne inférieure donnée dans l’équation 5.2.2.3 sera utilisée. Par conséquent, z = 1,645 conviendra. Autrement dit, avec une confiance de 95 %, on peut conclure que la différence entre les moyennes (concassé moins moulé) surpasse

Autrement dit, elle surpasse :
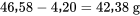
Formulé autrement, l’intervalle de confiance unilatéral à 95 % pour 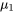 −
− 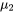 correspond à
correspond à
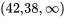
Les étudiant.e.s éprouvent parfois un certain malaise face au choix arbitraire qu’implique l’étiquetage des deux conditions dans une étude à deux échantillons. En réalité, les deux options peuvent être utilisés. Pour autant qu’on respecte ce choix tout au long du raisonnement, il n’affectera aucunement les conclusions tirées dans le monde réel. Dans l’exemple 5.5.2.2, si la condition « moulé » est désignée par le numéro 1 et la condition « concassé » par le numéro 2, l’intervalle de confiance la moyenne « moulé » moins la moyenne « concassé » est la suivante :
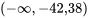
Concrètement, cet intervalle a exactement le même sens que celui de l’exemple.
Rappelons que les présentes méthodes s’appliquent lorsque des mesures uniques sont réalisées sur chaque élément de deux échantillons différents. Ceci contraste avec les questions relatives aux données appariées (où il y a des observations à deux variables sur un seul échantillon); nous reviendrons à ce cas plus tard.
