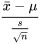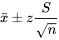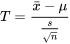5.2.1 Inférence pour une moyenne unique sur un petit échantillon
La principale limitation pratique à l’utilisation des méthodes évoquées dans les deux chapitres précédents, c’est que n doit être grand. Cette restriction résulte du fait que, si ce n’est pas le cas, il est impossible de conclure que la variable
5.2.1.1
est approximativement normale réduite. Donc, si on utilise machinalement la formule de l’intervalle de confiance pour un grand n
5.2.1.2
sur un petit échantillon, il s’avérera impossible d’évaluer le niveau de confiance réel. Autrement dit, pour un petit n, l’utilisation de z = 1,96 dans l’équation 5.2.1.2 ne génère généralement pas d’intervalles de confiance à 95 %. Sans condition supplémentaire, il n’y a ni moyen de savoir quelle confiance est associée à z = 1,96 ni moyen de savoir comment choisir z de façon à obtenir un niveau de confiance de 95 %.
Il y a un cas particulier et important pour lequel un raisonnement parallèle à celui de la partie 5 permet d’obtenir des méthodes d’inférence pour la moyenne d’un petit échantillon : lorsqu’on peut modéliser les observations en tant que variables aléatoires normales iid. Le cas des observations normales est pratique car, même si la variable 5.2.1.1 n’est pas normale réduite, sa distribution est connue et illustrée sous forme de tableau. Il s’agit de la distribution t de Student.
DÉFINITION 5.2.1.1 La distribution t de Student
La distribution t (de Student) avec un paramètre de degrés de liberté 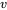 est une distribution de probabilité continue ayant une densité de probabilité
est une distribution de probabilité continue ayant une densité de probabilité
EXPRESSION 5.2.1.3
f(t)=\frac{\Gamma\left(\frac{v+1}{ 2}\right)}{\Gamma\left(\frac{v}{ 2}\right) \sqrt{\pi v}}\left(1+\frac{t^2}{v}\right)^{-(v+1) / 2}alttitlef(t)=\frac{\Gamma\left(\frac{v+1}{ 2}\right)}{\Gamma\left(\frac{v}{ 2}\right) \sqrt{\pi v}}\left(1+\frac{t^2}{v}\right)^{-(v+1) / 2}title
pour tout t.
Si une variable aléatoire présente une densité de probabilité donnée par l’équation 5.2.1.3, on dit qu’elle suit une distribution 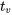 .
.
.
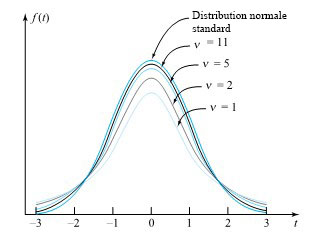
Le terme « Student » employé dans la définition 5.2.1.1 est en fait le nom de plume du premier statisticien à avoir découvert l’équation 5.2.1.3. Cette expression présente un caractère plutôt impressionnant. Le présent ouvrage ne prévoit aucun calcul direct à l’aide de cette formule. Toutefois, il s’avère utile de l’avoir à disposition pour esquisser quelques densités de probabilité t, afin de se faire une idée de leur forme. La figure 5.2.1.1 illustre les densités t pour les degrés de liberté 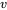 = 1, 2, 5, et 11, ainsi que la densité normale réduite.
= 1, 2, 5, et 11, ainsi que la densité normale réduite.
Distributions t et distribution normale réduite
Le message véhiculé par la figure 5.2.1.1 est que les densités de probabilité t ont la forme d’une cloche et sont symétriques par rapport à t = 0. Elles présentent un aspect plus plat que la densité normale réduite, mais s’en rapprochent de plus en plus à mesure que 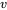 augmente. En fait, dans la plupart des cas, pour des
augmente. En fait, dans la plupart des cas, pour des 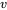 supérieurs à environ 30, la distribution t avec [latex]ν[/latex] degrés de liberté et la distribution normale standard sont impossibles à distinguer.
supérieurs à environ 30, la distribution t avec [latex]ν[/latex] degrés de liberté et la distribution normale standard sont impossibles à distinguer.
Généralement, pour calculer une probabilité associée à une distribution t, on n’utilise pas l’expression 5.2.1.3, car il n’existe pas d’antidérivée simple pour 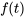 . On utilise plutôt des tables (ou des logiciels statistiques) pour évaluer les quantiles communs de la distribution t et ainsi obtenir des limites approximatives sur les types de probabilités nécessaires pour les tests d’hypothèse. La table A1.3 de l’annexe 1 des tables statistiques représente un tableau typique de quantiles t. Les colonnes représentent les probabilités cumulatives et les lignes, les valeurs du paramètre des degrés de liberté,
. On utilise plutôt des tables (ou des logiciels statistiques) pour évaluer les quantiles communs de la distribution t et ainsi obtenir des limites approximatives sur les types de probabilités nécessaires pour les tests d’hypothèse. La table A1.3 de l’annexe 1 des tables statistiques représente un tableau typique de quantiles t. Les colonnes représentent les probabilités cumulatives et les lignes, les valeurs du paramètre des degrés de liberté, 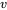 . Le corps de la table énumère les quantiles correspondants. À noter que la dernière ligne du tableau est une ligne «
. Le corps de la table énumère les quantiles correspondants. À noter que la dernière ligne du tableau est une ligne « 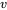 =∞ » (c.-à-d. distribution normale réduite).
=∞ » (c.-à-d. distribution normale réduite).
Exemple 5.2.1.1 Utilisation des tables de quantiles de distribution t
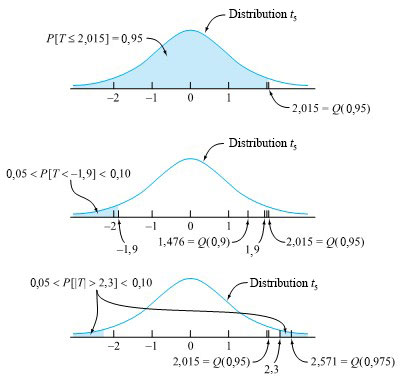
Soit T une variable aléatoire ayant une distribution t avec 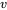 = 5 degrés de liberté. Trouvons d’abord le quantile 0,95 de la distribution de T, puis voyons ce que le tableau A1.3 révèle sur P [T < -1,9] et ensuite sur P [|T | > 2,3].
= 5 degrés de liberté. Trouvons d’abord le quantile 0,95 de la distribution de T, puis voyons ce que le tableau A1.3 révèle sur P [T < -1,9] et ensuite sur P [|T | > 2,3].
Tout d’abord, si l’on examine la ligne 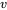 = 5 du tableau A1.3 sous la probabilité cumulative 0,95, on trouve 2,015 dans le corps du tableau. Autrement dit,
= 5 du tableau A1.3 sous la probabilité cumulative 0,95, on trouve 2,015 dans le corps du tableau. Autrement dit, 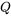 (0,95) = 2,015 ou (de manière équivalente) P [T ≤ 2,015] = 0,95.
(0,95) = 2,015 ou (de manière équivalente) P [T ≤ 2,015] = 0,95.
On notera alors que par symétrie,
P[T<-1,9]=P[T>1,9]=1-P[T \leq 1,9]alttitleP[T<-1,9]=P[T>1,9]=1-P[T \leq 1,9]title
En regardant la ligne 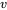 = 5 du tableau A1.3, on constate que 1,9 se situe entre les quantiles 0,90 et 0,95 de la distribution
= 5 du tableau A1.3, on constate que 1,9 se situe entre les quantiles 0,90 et 0,95 de la distribution 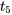 . Autrement dit,
. Autrement dit,
<img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e1890f6402fcf9259a7b0f0f04a0da1d.png" alt="0,90 < P[T \leq 1,9] \leq 0,95" title="0,90
Finalement :
<img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/aa11f0559ae54bcdeb34f81f860c2315.png" alt="0,05 < P[T<-1,9]<0,10" title="0,05 < P[T<-1,9]
Ensuite, en regardant la ligne  = 5 du tableau A1.3, on constate que 2,3 se situe entre les quantiles 0,95 et 0,975 de la distribution
= 5 du tableau A1.3, on constate que 2,3 se situe entre les quantiles 0,95 et 0,975 de la distribution 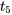 . Autrement dit,
. Autrement dit,
<img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/29569022f5ed215f07016795b932ebde.png" alt="0,95 < P[T \leq 2,3]<0,975" title="0,95 < P[T \leq 2,3]
donc
0,05<P[|T|>2,3]<0,10
Les trois calculs de cet exemple apparaissent à la figure 5.2.1.2.
La relation entre les expressions 5.2.1.3 et 5.2.1.1 qui permet de développer des méthodes d’inférence à petit n pour les observations normales se résume au fait que si un modèle normal iid convient,
5.2.1.4
suit une distribution t avec 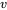 = n − 1 degrés de liberté. (Ce résultat cohérent avec le principe de base utilisé dans les deux chapitres précédents : pour un grand n,
= n − 1 degrés de liberté. (Ce résultat cohérent avec le principe de base utilisé dans les deux chapitres précédents : pour un grand n, 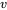 est grand, donc la distribution
est grand, donc la distribution 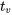 devient approximativement normale réduite; et pour un grand n, la variable 5.2.1.4 a déjà été traitée comme étant approximativement normale réduite.)
devient approximativement normale réduite; et pour un grand n, la variable 5.2.1.4 a déjà été traitée comme étant approximativement normale réduite.)
Puisque la variable 5.2.1.4 peut, dans des circonstances favorables, être traitée comme une variable aléatoire altt_{n-1}alttitlet_{n-1}title, il est possible de reprendre exactement ce qui a été fait à la partie 5 pour trouver des méthodes permettant d’établir des intervalles de confiance et d’effectuer des tests d’hypothèse. Autrement dit, si on peut considérer qu’un mécanisme de génération de données équivaut fondamentalement à tirer des observations indépendantes d’une distribution normale unique, un intervalle de confiance bilatéral pour µ comporte des des bornes
EXPRESSION 5.2.1.5 Bornes de distribution normale de confiance pour µ
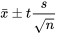
où t est choisie de sorte que la distribution 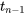 attribue une probabilité correspondant au niveau de confiance souhaité à l’intervalle compris entre -t et t. De même, l’hypothèse nulle
attribue une probabilité correspondant au niveau de confiance souhaité à l’intervalle compris entre -t et t. De même, l’hypothèse nulle
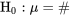
peut être testée à l’aide de la statistique
EXPRESSION 5.2.1.6 Statistique de test de la distribution normale pour µ
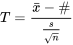
et d’une distribution 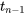 de référence.
de référence.
Sur le plan opérationnel, la seule différence entre les méthodes d’inférence exposées ici et les méthodes à grand échantillon des deux chapitres précédents est qu’au lieu d’utiliser les quantiles et les probabilités de la distribution normale réduite, on utilise ceux de la distribution 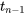 . Sur le plan conceptuel, les propriétés de confiance et de signification nominales ne sont pertinentes en pratique que sous la condition supplémentaire d’une distribution sous-jacente raisonnablement normale. Avant d’utiliser les expressions 5.2.1.5 et 5.2.1.6, il est recommandé d’examiner la pertinence du modèle de distribution normale.
. Sur le plan conceptuel, les propriétés de confiance et de signification nominales ne sont pertinentes en pratique que sous la condition supplémentaire d’une distribution sous-jacente raisonnablement normale. Avant d’utiliser les expressions 5.2.1.5 et 5.2.1.6, il est recommandé d’examiner la pertinence du modèle de distribution normale.
Exemple 5.2.1.2 Bornes de confiance pour la moyenne de la durée de vie d’un ressort sur un petit échantillon
Une partie d’un ensemble de données de W. Armstrong (figurant dans Analysis of Survival Data, de Cox and Oakes) fournit le nombre de cycles jusqu’à la rupture de 10 ressorts du même type sous une contrainte de 950 N/mm2. Ces observations relatives à la durée de vie des ressorts se retrouvent dans le tableau 5.2.1.1 en unités de 1 000 cycles.

Tableau 5.2.1.1. Dans ce scénario, on pourrait se demander : « Quelle est la durée de vie moyenne d’un ressort soumis à une contrainte de 950 N/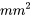 ? » Comme il n’y a que de n = 10 observations, la méthode pour les grands échantillons vue au module 5.1 ne s’applique pas. Seule la méthode indiquée par l’expression 5.2.1.5 peut potentiellement être utilisée, et pour qu’elle convienne, les durées de vie doivent être distribuées normalement.
? » Comme il n’y a que de n = 10 observations, la méthode pour les grands échantillons vue au module 5.1 ne s’applique pas. Seule la méthode indiquée par l’expression 5.2.1.5 peut potentiellement être utilisée, et pour qu’elle convienne, les durées de vie doivent être distribuées normalement.
Faute de disposer d’expérience pertinente en ingénierie des matériaux, il apparaît difficile de spéculer a priori sur la justesse d’un modèle de durée de vie normale dans ce contexte. Néanmoins, il reste possible d’examiner les données du tableau 5.2.1.1 pour vérifier si elles présentent un écart important par rapport à la distribution normale. La figure 5.2.1.3 illustre un tracé normal des données, qui suggère que les données semblent être normalement distribuées.
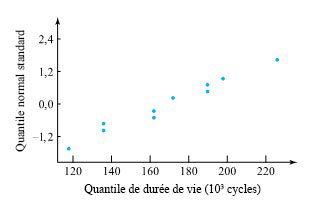
Pour les 10 durées de vie,  = 168,3(× 10³ cycles) et s = 33,1(×10³ cycles). Ainsi, pour estimer la durée de vie moyenne du ressort, ces valeurs peuvent être utilisées dans l’expression 5.2.1.5, avec une valeur de t convenablement choisie. En utilisant, par exemple, un niveau de confiance de 90 % et un intervalle bilatéral, t correspond au quantile 0,95 de la distribution t avec
= 168,3(× 10³ cycles) et s = 33,1(×10³ cycles). Ainsi, pour estimer la durée de vie moyenne du ressort, ces valeurs peuvent être utilisées dans l’expression 5.2.1.5, avec une valeur de t convenablement choisie. En utilisant, par exemple, un niveau de confiance de 90 % et un intervalle bilatéral, t correspond au quantile 0,95 de la distribution t avec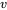 degrés de liberté. Autrement dit, on utilise la distribution
degrés de liberté. Autrement dit, on utilise la distribution 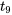 et on choisit t > 0 de sorte que
et on choisit t > 0 de sorte que
[latex]P[-t< \text{une variable aléatoire } t_9 < t] = 0,90[/latex]
En consultant le tableau A1.3, le choix t = 1,833 s’impose. Ainsi, l’intervalle de confiance bilatéral de 90 % pour µ comporte les bornes
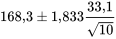
soit
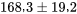
c.-à-d.
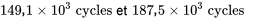
Vérification des tracés normaux
Comme l’illustre l’exemple 5.2.1.2, produire un tracé normal des données pour vérifier sommairement la plausibilité d’une distribution normale sous-jacente constitue une pratique valable, utilisée à maintes reprises dans ce manuel. Cependant, il faut éviter de s’attendre à plus que la méthode ne le justifie. Il vaut assurément mieux l’utiliser plutôt que de présumer, sans preuve, qu’une distribution est normale, ce qui pourrait ne pas être le cas. Mais il faut aussi reconnaître que lorsqu’elle est utilisée sur de petits échantillons, la méthode fournit rarement des indications décisives quant à la pertinence d’un modèle normal. Les petits échantillons issus de distributions normales ne présenteront souvent que des tracés normaux d’apparence légèrement linéaire. Parallèlement, les petits échantillons provenant de distributions assez anormales peuvent souvent présenter des courbes normales relativement linéaires. En somme, en raison de la variabilité de l’échantillonnage, les petits échantillons ne fournissent pas beaucoup d’informations sur la forme de la distribution sous-jacente. Tout ce que l’on peut attendre d’un tracé normal préliminaire sur un petit échantillon, tel que celui de l’exemple 5.2.1.2, c’est un avertissement en cas d’écart flagrant par rapport à la normalité –une distribution sous-jacente beaucoup plus lourde dans les queues qu’une distribution normale (c’est-à-dire produisant plus de valeurs extrêmes qu’une forme normale ne le ferait).
Tests d’hypothèses pour 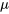 sur petits échantillons
sur petits échantillons
L’exemple 5.2.1.2 montre comment utiliser la formule de l’intervalle de confiance 5.2.1.5, mais pas comment faire un test d’hypothèse (équation 5.2.1.6). Puisque la méthode sur petit échantillon s’apparente exactement à la méthode sur grand échantillon du module 5.1 (en utilisant la distribution t plutôt que la distribution normale réduite), et que la source d’où proviennent les données n’indique aucune valeur de µ qui pourrait d’emblée constituer l’hypothèse nulle, l’utilisation de la méthode correspondant à l’expression 5.2.1.6 ne sera pas illustrée à ce stade.