5.1.6 Signification statistique, estimation et importance pratique
Quelques commentaires concernant les tests d’hypothèse et l’estimation
L’estimation d’un l’intervalle de confiance et le test d’hypothèse sont les deux formes d’inférence statistique formelle les plus couramment utilisées. À la lumière de leur présentation, il convient de faire quelques observations comparatives sur leur utilité pratique et, ce faisant, de faire état d’une orientation en matière d’estimation dont il sera question dans la majeure partie du traitement de l’inférence formelle dans le reste de cet ouvrage.
La plupart du temps, on se demande « Quelle est la valeur du paramètre? » plutôt que « Le paramètre équivaut-il à une valeur hypothétique? » Pour répondre à la première question, c’est à l’estimation de l’intervalle de confiance et non aux tests d’hypothèse qu’il faudra recourir. Un intervalle de confiance pour la moyenne du couple de rupture de 9,9 à 13,1 po oz indique quelles valeurs de µ semblent plausibles. Un infime seuil de signification observé dans le test de  : µ = 33,5 indique seulement que les données s’opposent manifestement à la possibilité que µ = 33,5, mais il ne donne pas d’indice sur la valeur probable de µ.
: µ = 33,5 indique seulement que les données s’opposent manifestement à la possibilité que µ = 33,5, mais il ne donne pas d’indice sur la valeur probable de µ.
Signification statistique et importance pratique Le fait que les tests d’hypothèse ne donnent aucune indication utile sur les valeurs plausibles des paramètres peut être occulté par une interprétation maladroite du langage semi-standard. Par exemple, il est courant dans certains domaines d’appeler les valeurs p inférieures à 0,05 « statistiquement significatives » et celles inférieures à 0,01 « hautement significatives ». Le piège dans ce type d’utilisation est que « significatif » peut être compris, à tort, comme synonyme de « grande conséquence pratique » et que la valeur p peut être interprétée, à tort, comme une mesure de l’écart entre un paramètre et la valeur énoncée dans l’hypothèse nulle. L’une des raisons pour lesquelles cette interprétation est faussée, c’est que le seuil de signification observé dans un test dépend non seulement de l’écart entre [latex]H_0[/latex] et la réalité, mais aussi de la taille de l’échantillon. Avec un échantillon de taille suffisante, tout écart par rapport à H0 peut être considéré comme « hautement significatif », qu’il ait une importance pratique ou non.
Exemple 5.1.6.1 Signification statistique et importance pratique dans le cadre d’un essai réalisé par un organisme de réglementation
L’article de presse de la figure 5.1.6.1 illustre parfaitement les points précédents. Le fabricant du Pass Master a effectué suffisamment de tests physiques de consommation d’essence (avec un n suffisamment élevé) pour produire une valeur p inférieure à 0,05 afin de tester l’hypothèse nulle de l’absence d’amélioration du kilométrage. Autrement dit, il a obtenu un résultat « statistiquement significatif ».
Cependant, l’amélioration du kilométrage réel rapportée reste « faible mais réelle », puisqu’elle s’élève à environ 0,8 mpg. Le fait que cette amélioration revête une importance pratique ou non reste une question nettement distincte du résultat du test d’hypothèse. Si on dispose d’un intervalle de confiance pour la moyenne d’amélioration du kilométrage,
on se trouve en meilleure posture pour juger de l’importance pratique
que si on n’a qu’une valeur p inférieure à 0,05.

Exemple 5.1.6.2 (suite)
Pour illustrer l’effet de la taille de l’échantillon sur le seuil de signification observé, reprenons l’exemple du couple de rupture et examinons deux échantillons hypothétiques, l’un de n = 25 et l’autre de n = 100, mais tous deux donnant  = 32,5 po oz et s = 5,1 po oz.
= 32,5 po oz et s = 5,1 po oz.
Pour les essais  : µ = 33,5 avec
: µ = 33,5 avec  : µ<33,5, le premier échantillon hypothétique donne :
: µ<33,5, le premier échantillon hypothétique donne :
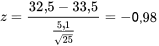
avec un seuil de signification observé associé de
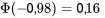
Le deuxième échantillon hypothétique donne
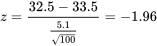
avec une valeur p correspondante de
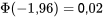
La taille du deuxième échantillon étant plus importante, celui-ci démontre plus clairement que la moyenne du couple de démarrage est inférieure à 33,5 po oz. Mais la meilleure supposition en fonction des données concernant la différence entre µ et 33,5 est  dans les deux cas. Or, c’est précisément l’ampleur de la différence entre µ et 33,5 po oz qui revêt une importance primordiale en ingénierie.
dans les deux cas. Or, c’est précisément l’ampleur de la différence entre µ et 33,5 po oz qui revêt une importance primordiale en ingénierie.
En outre, il importe de savoir qu’en plus de sa fonction principale, qui consiste à fournir un intervalle de valeurs plausibles pour un paramètre, l’intervalle de confiance apporte également des informations relatives au test d’hypothèse. Par exemple, un intervalle de confiance à 95 % pour un paramètre contient toutes les valeurs du paramètre pour lesquelles les tests d’hypothèse effectués à l’aide des données disponibles produiraient des valeurs p supérieures à 5 %. (Les valeurs non couvertes par l’intervalle auraient des valeurs p associées inférieures à 5 %.)
Exemple 6.1.6.3 (suite)
Au chapitre 5.1.1, il a été démontré que l’intervalle de confiance unilatéral à 90 % pour la moyenne du couple de rupture des disques durs défectueux est de (-∞, 12,8). Cela signifie que pour toute valeur # supérieure à 12,8 po oz, un test d’hypothèse de  : µ = # avec
: µ = # avec  : µ < # produirait une valeur p inférieure à 0,1. Ainsi, il apparaît clairement que le seuil de signification observé correspondant à l’hypothèse nulle
: µ < # produirait une valeur p inférieure à 0,1. Ainsi, il apparaît clairement que le seuil de signification observé correspondant à l’hypothèse nulle  : µ = 33,5 est inférieur à 0,1. (En fait, comme il a été vu plus haut dans ce chapitre, la valeur p est de 0 à la deuxième décimale.) En termes plus simples, l’intervalle (-∞, 12,8) est encore loin de contenir 33,5 po oz, ce qui rend une telle valeur de µ peu plausible.
: µ = 33,5 est inférieur à 0,1. (En fait, comme il a été vu plus haut dans ce chapitre, la valeur p est de 0 à la deuxième décimale.) En termes plus simples, l’intervalle (-∞, 12,8) est encore loin de contenir 33,5 po oz, ce qui rend une telle valeur de µ peu plausible.
La réflexion menée ici pourrait bien soulever la question suivante : « Dans la pratique, à quoi les tests d’hypothèse peuvent-ils servir? » Voici quelques réponses pertinentes à cette question :
1. D’une certaine manière, les valeurs p peuvent servir à évaluer dans quelle mesure les données disponibles sont peu probantes. Un seuil de signification élevé signifie qu’il faut obtenir plus d’informations pour parvenir à un jugement décisif.
2. Parfois, la loi impose l’utilisation de tests d’hypothèse dans le cadre d’une démonstration de conformité ou d’efficacité. (C’était le cas dans l’exemple 5.1.6.2, où la commercialisation du Pass Master exigeait une démonstration légale de la réduction de la consommation d’essence.)
3. Dans certains cas, l’utilisation de tests d’hypothèses dans un cadre de prise de décision se révèle nécessaire et pertinente. (L’échantillonnage pour acceptation en est un exemple : à partir d’informations tirées d’un échantillon d’articles provenant d’un lot volumineux, on doit décider si on réceptionne le lot ou non.)
4. À titre de preuves supplémentaire et de compléments aux rapports ou aux résultats de publications scientifiques.
Ainsi, lorsque les tests d’hypothèses sont correctement interprétés et utilisés, ils trouvent leur place dans la pratique de l’ingénierie. Par conséquent, bien que le reste de cet ouvrage mette l’accent sur l’estimation plutôt que sur les tests d’hypothèse, on ne peut négliger les méthodes utilisées dans le cadre des tests d’hypothèse.
