5.1.5 Test d’hypothèse et décision statistique
La logique à laquelle fait référence ce chapitre s’applique parfois à un contexte de prise de décision, où l’on fait appel à des données pour orienter le choix entre deux options concurrentes. Dans de tels cas, un cadre décisionnel explicite accompagne généralement l’analyse statistique formelle, ce qui entraîne le recours à une terminologie et à des schémas de pensée supplémentaires.
Dans certains contextes décisionnels, on peut envisager que les deux avenues sont liées à l’hypothèse nulle et à l’hypothèse alternative. Par exemple, dans le scénario du remplissage de pots, 
: µ = 139,8 g pourrait correspondre à la décision « ne pas toucher à la procédure », et 
: µ ≠ 139,8 pourrait correspondre à la décision « ajuster la procédure ». Dans ce genre de contexte, il y a deux types d’erreurs distincts qui peuvent se produire.
DÉFINITION 5.1.5.1 Erreur de type 1
Lorsqu’on recoure à un test d’hypothèse dans le cadre d’une prise de décision, le fait de se prononcer en faveur de alors que la réalité correspond plutôt à constitue une erreur de type 1.
DEFINITION 5.1.5.2 Erreur de type 2
Lorsqu’on utilise un test d’hypothèse dans le cadre d’une prise de décision, le fait de se prononcer en faveur de alors que la réalité correspond plutôt à constitue une erreur de type 2.
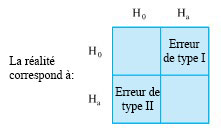
Le contenu de ces deux définitions est représenté dans le tableau 2 × 2 illustré à la figure 5.1.5.1. Dans l’exemple du remplissage de pots, l’ajustement d’une procédure correcte constituerait une erreur de type 1. En revanche, une erreur de type 2 consisterait à ne pas ajuster une procédure hors cible.
On utilise les tests d’hypothèse pour parvenir à une décision en choisissant une valeur critique, et si le seuil de signification observé se révèle inférieur à la valeur critique (rendant ainsi l’hypothèse nulle peu plausible), on tranche en faveur de . Autrement, on applique l’option correspondant à . La valeur critique relative au seuil de signification observé représente finalement la probabilité initiale qu’on se prononce en faveur de , probabilité calculée sous réserve de la véracité de . Ce concept fait l’objet d’une terminologie spécifique.
DÉFINITION 5.1.5.3 Seuil de signification
Lorsqu’un test d’hypothèse est utilisé dans un contexte décisionnel, la valeur critique qui sépare les seuils de signification élevés pour lesquels sera validée des seuils de signification inférieurs pour lesquels se verra rejetée en faveur de , se nomme probabilité d’erreur de type 1, ou seuil de signification. On utilise généralement le symbole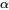 
pour désigner la probabilité d’erreur de type 1.
En pratique, 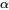est généralement un petit nombre (comme 0,1, 0,05 ou même 0,01), ce qui permet d’introduire une certaine inertie en faveur de H0 dans le processus de prise de décision. (Une telle pratique garantit la faible fréquence des erreurs de type 1. Mais, parallèlement, il en résulte une asymétrie dans le traitement de et de qui s’avère parfois injustifiée.)
La définition 5.1.5.2 et la figure 5.1.5.1 établissent clairement que les erreurs de type 1 ne constituent pas la seule possibilité peu souhaitable. Il faut également prendre en considération la possibilité d’erreurs de type 2.
DÉFINITION 5.1.5.4 Erreur de type 2
Lorsque des tests d’hypothèse sont utilisés dans un contexte décisionnel, la probabilité – calculée en supposant qu’une valeur particulière du paramètre décrite par est valide – que le seuil de signification observé se révèle supérieur à α (c’est-à-dire que ne soit pas rejetée) se nomme probabilité d’erreur de type 2. On utilise généralement le symbole β
pour représenter la probabilité d’erreur de type 2. Il existe un concept appelé « puissance statistique », qui correspond à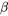 
.
Dans la plupart des méthodes d’essai étudiées dans cet ouvrage, le calcul de β excède la portée de l’introduction limitée aux probabilités fournie à la partie 4. Mais la tâche peut être effectuée pour la situation simple où l’on connaît σ évoquée lors de l’introduction du thème des tests d’hypothèse. De plus, quelques calculs de ce type vous procureront une certaine intuition représentative de ce qui prévaut généralement, du moins sur le plan qualitatif.
Example 5.1.5.1 (suite)
Considérons à nouveau la procédure de remplissage et le test et 
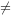. Cette fois, imaginons que, demain, on recourra à un test d’hypothèse avec n = 25
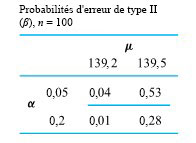
afin de déterminer s’il faut modifier ou non la procédure. Les probabilités d’erreur de type 2, calculées en présumant que µ = 139,5 et µ = 139,2 pour les tests utilisant α = 0,05 et α = 0,2, seront comparées.
On se penche d’abord sur α = 0,05. La décision sera prise en faveur de si la valeur p est supérieure à 0,05. En d’autres termes, la décision est favorable à l’hypothèse nulle si la valeur observée de Z donnée dans l’équation correspond à
|z| < 1,96
ce qui revient à dire
139,8-1,96(0,32)<\bar{x}<139,8+1,96(0,32)
Autrement dit, on veut déterminer si :
5.1.5.1<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/fe8f117cedd54f9dd050c132cca373d1.png » alt= »139,2<\bar{x}<140,4″ title= »139,2<\bar{x}
Si µ décrite par (avec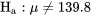 
) représente la véritable moyenne de la procédure,
n’est pas approximativement normale avec une moyenne de 139,8 et un écart-type de 0,32, mais plutôt approximativement normale avec une moyenne de µ et un écart-type de 0,32. Ainsi, pour une telle valeur de µ, l’inégalité 5.1.5.1 et la définition 5.1.5.4 démontrent que le β correspondant représente la probabilité que la distribution normale correspondante attribue à la possibilité que 139,2 < < 140,4. Ceci est illustré dans la figure 5.1.5.2 pour les deux moyennes µ = 139,5 et µ = 139,2.
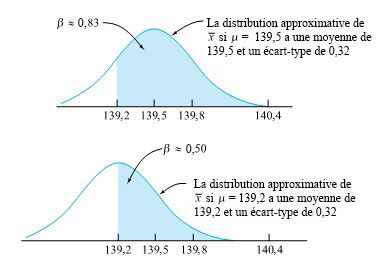
Pour calculer les cotes z correspondant à = 139,2 et = 140,4 avec des moyennes de 139,5 et de 139,2 et un écart-type de 0,32, il suffit de consulter une table de distribution normale standard, ce qui a été fait pour fournir les deux β de la figure 5.1.5.2.
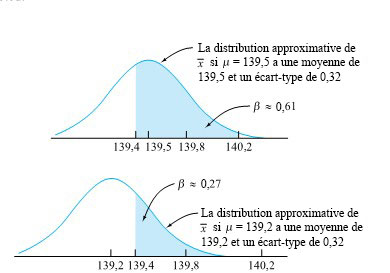
Le raisonnement parallèle pour la situation avec α = 0,2 se fait comme suit : la décision sera prise en faveur de si la valeur p est supérieure à 0,2. En d’autres termes, la décision sera favorable à si |z| < 1,28, soit si :
139,4 < < 140,2
Si µ décrite par représente la véritable moyenne de la procédure, est approximativement normale avec une moyenne µ et un écart type de 0,32. Ainsi, le β correspondant représente la probabilité que cette distribution normale attribue à la possibilité que 139,4 < < 140,2. La figure 5.1.5.3 l’illustre pour les deux moyennes µ = 139,5 et µ = 139,2, avec les probabilités d’erreur de type 2 correspondantes β = 0,61 et β = 0,27.
Les calculs représentés par les deux figures sont résumés dans le tableau 5.1.5.1. On peut remarquer deux caractéristiques dans ce tableau. Premièrement, les valeurs de β pour α = 0,05 sont plus élevées que celles pour α = 0,2. Si l’on ne veut courir qu’un risque de 5 % de décider (à tort) d’ajuster une procédure qui atteint sa cible, le prix à payer est d’avoir une plus grande probabilité de ne pas reconnaître que la procédure est hors cible. Deuxièmement, les valeurs de β pour µ = 139,2 sont plus petites que les valeurs β pour µ = 139,5. Plus la procédure de remplissage s’éloigne de la cible, plus il est probable qu’on détecte cet écart par rapport à la cible.
Le récit présenté dans le tableau 5.1.5.1 s’applique de manière qualitative à toutes les utilisations de tests d’hypothèse dans des contextes de prise de décision. Plus s’éloigne de la vérité, plus le β correspondant diminue. En outre, de petits α entraînent de grands β, et vice-versa.
Effet de la taille de l’échantillon sur 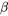s
Il y a un autre élément de ce panorama qui joue un rôle important dans la détermination des probabilités d’erreur : la taille de l’échantillon. Pour un α donné, si la taille d’un échantillon peut être augmentée, les β correspondants peuvent être réduits. Reprenons les calculs de l’exemple précédent, en supposant cette fois que n = 100 au lieu de 25. Le tableau 5.1.5.2 illustre les probabilités d’erreur de type 2 censées en résulter; en comparant avec le tableau 5.1.5.1, on voit l’effet de la taille de l’échantillon dans l’exemple de la procédure de remplissage.
Analogie entre
un test d’hypothèse et
un procès criminel
Pour mieux comprendre la logique communément appliquée aux tests d’hypothèse dans le cadre d’un processus de prise de décision, on peut faire une analogie avec un procès criminel. Dans un procès criminel, deux hypothèses s’opposent :
: la personne accusée est innocente
: la personne accusée est coupable
Des preuves, dont le rôle se rapproche de celui des données utilisées dans les tests, sont recueillies et utilisées pour trancher entre les deux hypothèses. Deux types d’erreurs éventuelles surviennent lors d’un procès criminel : la possibilité de condamner une personne innocente (erreur de type 1) et la possibilité d’acquitter une personne coupable (erreur de type 2). Un procès criminel constitue une situation où les deux types d’erreur ont
des conséquences résolument différentes et où les deux hypothèses subissent un traitement asymétrique. La présomption a priori est favorable à , l’innocence de la personne accusée. Afin de maintenir un faible risque de fausse condamnation (c’est-à-dire un α faible), des preuves accablantes s’avèrent nécessaires pour obtenir une condamnation, à l’instar de l’utilisation d’un α faible dans les tests, qui nécessite des valeurs extrêmes de la statistique de test pour infirmer . L’une des conséquences de cette procédure dans les procès criminels, c’est qu’il existe une probabilité substantielle qu’un individu coupable soit acquitté, au même titre que les faibles α produisent des β élevés dans les contextes de test d’hypothèse.
Ce parallèle entre les tests d’hypothèse et les procès criminels peut se révéler utile, à condition de ne pas en abuser. Il ne s’applique pas à toutes les utilisations des tests d’hypothèse, et rares sont les scénarios d’ingénierie suffisamment simples pour se réduire à un simple choix entre et . Les applications judicieuses des tests d’hypothèse ne constituent souvent que des étapes de « l’évaluation de la preuve » dans le cadre d’une tâche aux nombreuses facettes, fondée sur des données, nécessaire à la résolution d’un problème d’ingénierie. De plus, même lorsqu’un problème réel peut se réduire à la simple question de choisir entre et , cela ne veut pas dire que la logique dicte forcément qu’il faut choisir un α petit. Dans certains contextes en ingénierie, les conséquences d’une erreur de type 2 sur le plan pratique font en sorte qu’une prise de décision rationnelle doit trouver un équilibre entre un petit α et un petit β, deux possibilités qui s’opposent l’une à l’autre.