5.1.3 Modèle de synthèse de tests d’hypothèse en cinq étapes
Modèle de synthèse de tests d’hypothèse en cinq étapes
Il est utile de définir un modèle étape par étape pour organiser les comptes rendus des tests d’hypothèse. Celui qui sera utilisé dans ce manuel comprend les cinq étapes suivantes :
Étape 1 Énoncer l’hypothèse nulle.
Étape 2 Énoncer l’hypothèse alternative.
Étape 3 Énoncer les critères du test, c’est-à-dire, donner la formule de la statistique de test (en introduisant uniquement une valeur supposée de l’hypothèse nulle, mais aucune information sur l’échantillon) et la distribution de référence. Ensuite, indiquer, en termes généraux, les valeurs observées de la statistique de test
qui constitueront la preuve contre l’hypothèse nulle.
Étape 4 Montrer les calculs basés sur l’échantillon.
Étape 5 Signaler le seuil de signification observé et, dans la mesure du possible, expliquer ce qu’il signifie pour le problème d’ingénierie.
Exemple 5.1.3.1 Test d’hypothèse concernant le niveau moyen de remplissage
Le modèle de test d’hypothèse en cinq étapes peut être utilisé pour résumer la discussion précédente sur le processus de remplissage.
1.  : µ = 139,8 g.
: µ = 139,8 g.
2.  : µ
: µ 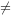 139,8 g.
139,8 g.
3. La statistique de test est la suivante :
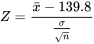
La distribution de référence est la distribution normale réduite, et de grandes valeurs observées |z| constitueront une preuve contre  .
.
4. L’échantillon donne
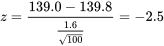
5. Le seuil de signification observé est :
![\begin{aligned} & P[\text { une variable normale réduite } \leq-2,5] \\ & \quad+P[\text { une variable normale réduite } \geq 2,5] \\ & \quad=P[\mid \text { une variable normale réduite } \mid \geq 2,5] \\ & \quad=0,01 \end{aligned} \begin{aligned} & P[\text { une variable normale réduite } \leq-2,5] \\ & \quad+P[\text { une variable normale réduite } \geq 2,5] \\ & \quad=P[\mid \text { une variable normale réduite } \mid \geq 2,5] \\ & \quad=0,01 \end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/1ea01517eb8ce96743c075f3c7345cb8.png)
Il s’agit d’un appui raisonnablement faible en faveur de l’hypothèse nulle. Par conséquent, il s’agit d’un appui raisonnablement solide que le niveau de remplissage moyen n’est pas conforme à la cible.
