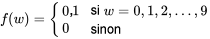4.2.4 Théorème central limite
Effet central limite
L’une des statistiques les plus fréquemment utilisées dans les applications d’ingénierie est la moyenne de l’échantillon. Nous avons déjà évoqué les équations pour la moyenne et la variance de la distribution de probabilité d’une moyenne d’échantillon ou d’une observation unique lorsque le modèle de variables iid s’applique. L’un des faits les plus utiles de la probabilité appliquée est que si la taille de l’échantillon est raisonnablement grande, il est également possible d’approximer la forme de la distribution de probabilité de 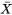 , quelle que soit la forme de la distribution sous-jacente des observations individuelles. Autrement dit, le fait suivant est avéré :
, quelle que soit la forme de la distribution sous-jacente des observations individuelles. Autrement dit, le fait suivant est avéré :
.
Proposition 4.2.4.1 Théorème central limite
Soient 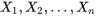 des variables aléatoires iid (avec une moyenne
des variables aléatoires iid (avec une moyenne  et une variance
et une variance  ). Pour des échantillons à grand
). Pour des échantillons à grand 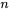 , la variable
, la variable 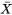 est approximativement normalement distribuée. (En d’autres termes, on peut approximer les probabilités de
est approximativement normalement distribuée. (En d’autres termes, on peut approximer les probabilités de 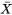 avec une distribution normale de moyenne
avec une distribution normale de moyenne  et de variance
et de variance 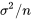 .)
.)
.
La preuve de la proposition 4.2.4.1 dépasse le cadre de ce manuel, mais on peut en saisir intuitivement la notion à l’aide d’un exemple.
Exemple 4.2.4.1 Effet central limite et moyenne d’un échantillon de numéros de série d’outils (suite)
Reprenons l’exemple de la section 3.2.1.2 concernant le dernier chiffre du numéro de série d’outils pneumatiques sélectionnés de manière essentiellement aléatoire. Supposons que
.
 le dernier chiffre du numéro de série observé lundi prochain à 9 h.
le dernier chiffre du numéro de série observé lundi prochain à 9 h. le dernier chiffre du numéro de série observé le lundi suivant à 9 h.
le dernier chiffre du numéro de série observé le lundi suivant à 9 h.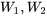 sont indépendantes, chacune avec la fonction de probabilité marginale :
sont indépendantes, chacune avec la fonction de probabilité marginale :4.2.4.1
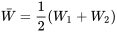 a la fonction de probabilité donnée au tableau 4.2.4.1 et illustrée à la figure 4.2.4.2.
a la fonction de probabilité donnée au tableau 4.2.4.1 et illustrée à la figure 4.2.4.2.
.
.

.
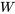 et une taille d’échantillon de
et une taille d’échantillon de 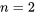 , la distribution de probabilité de
, la distribution de probabilité de 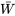 commence à prendre une forme de cloche – à tout le moins, plus que la distribution sous-jacente. La raison en est claire. Plus on s’éloigne de la moyenne ou de la valeur centrale de
commence à prendre une forme de cloche – à tout le moins, plus que la distribution sous-jacente. La raison en est claire. Plus on s’éloigne de la moyenne ou de la valeur centrale de 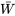 , moins il y a de combinaisons de
, moins il y a de combinaisons de  et
et 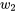 qui peuvent produire une valeur donnée de
qui peuvent produire une valeur donnée de 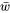 . Par exemple, pour que
. Par exemple, pour que  , il faut que
, il faut que  et
et 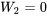 – autrement dit, il faut non pas une, mais deux valeurs extrêmes. En revanche, il existe 10 combinaisons différentes de
– autrement dit, il faut non pas une, mais deux valeurs extrêmes. En revanche, il existe 10 combinaisons différentes de  et
et 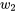 qui produisent
qui produisent 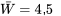 .
.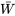 avec de grandes tailles d’échantillons
avec de grandes tailles d’échantillons 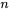 . Mais ce travail est fastidieux, et pour indiquer plus ou moins comment l’effet central limite prend le dessus au fur et à mesure que
. Mais ce travail est fastidieux, et pour indiquer plus ou moins comment l’effet central limite prend le dessus au fur et à mesure que 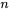 grossit, il suffit d’approximer la distribution de
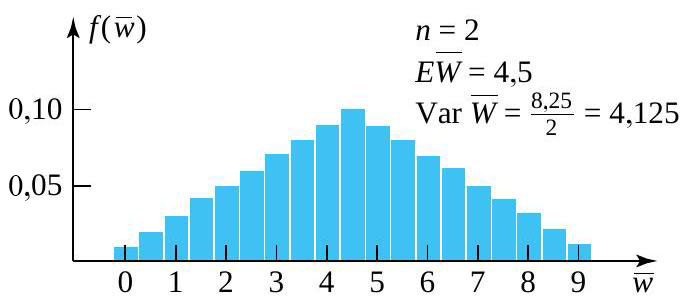
grossit, il suffit d’approximer la distribution de 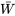 en simulant un échantillon de grande taille. À cette fin, regardons l’histogramme de fréquence (figure 4.2.4.3) de 1 000 ensembles de valeurs pour les variables iid
en simulant un échantillon de grande taille. À cette fin, regardons l’histogramme de fréquence (figure 4.2.4.3) de 1 000 ensembles de valeurs pour les variables iid 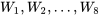 (avec une distribution marginale qui a été simulée et chaque ensemble pondéré pour produire 1 000 valeurs simulées de
(avec une distribution marginale qui a été simulée et chaque ensemble pondéré pour produire 1 000 valeurs simulées de 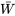 avec
avec 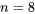 . Remarquez le caractère en forme de cloche du graphique. (La moyenne simulée de
. Remarquez le caractère en forme de cloche du graphique. (La moyenne simulée de 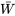 était de
était de 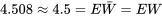 , alors que la variance de
, alors que la variance de 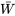 était de
était de 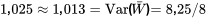 , en étroite concordance avec les formules.)
, en étroite concordance avec les formules.)
.
Taille de l’échantillon et effet central limite
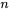 » dans la proposition 4.2.4.1 n’est pas évident. En réalité, la taille de l’échantillon nécessaire pour que
» dans la proposition 4.2.4.1 n’est pas évident. En réalité, la taille de l’échantillon nécessaire pour que 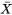 puisse être considérée comme essentiellement normale dépend de la forme de la distribution sous-jacente des observations individuelles. Les distributions sous-jacentes ayant des formes résolument non normales requièrent des valeurs un peu plus élevées de
puisse être considérée comme essentiellement normale dépend de la forme de la distribution sous-jacente des observations individuelles. Les distributions sous-jacentes ayant des formes résolument non normales requièrent des valeurs un peu plus élevées de 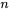 . Mais dans la plupart des applications d’ingénierie,
. Mais dans la plupart des applications d’ingénierie, 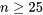 est généralement suffisant pour que
est généralement suffisant pour que 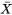 soit essentiellement normale pour la majorité des mécanismes de génération de données. (Les exceptions sont celles qui sont sujettes à la production occasionnelle de valeurs très éloignées de la réalité.) En effet, comme le suggère l’exemple 4.2.4.2, dans de nombreux cas
soit essentiellement normale pour la majorité des mécanismes de génération de données. (Les exceptions sont celles qui sont sujettes à la production occasionnelle de valeurs très éloignées de la réalité.) En effet, comme le suggère l’exemple 4.2.4.2, dans de nombreux cas 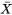 est essentiellement normale pour des tailles d’échantillon très inférieures à 25.
est essentiellement normale pour des tailles d’échantillon très inférieures à 25.Exemple 4.2.4.2 Exigence en matière de délai de vente de timbres.
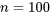 durées de service excessives pour obtenir :
durées de service excessives pour obtenir :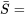 le temps moyen de l’échantillon (au-dessus du seuil de
le temps moyen de l’échantillon (au-dessus du seuil de 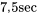 ) nécessaire pour réaliser les 100 prochaines ventes de timbres.
) nécessaire pour réaliser les 100 prochaines ventes de timbres.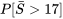 17]" title="P[\bar{S}>17]" class="latex mathjax">.
17]" title="P[\bar{S}>17]" class="latex mathjax">. est plausible pour les temps de service excessifs individuels
est plausible pour les temps de service excessifs individuels 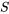 . Ainsi, on obtient
. Ainsi, on obtient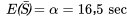
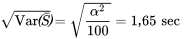
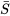 , selon nos équations. En outre, en tenant compte du fait que
, selon nos équations. En outre, en tenant compte du fait que 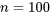 est grand, la table de probabilité normale peut être utilisée pour calculer les probabilités approximatives de
est grand, la table de probabilité normale peut être utilisée pour calculer les probabilités approximatives de 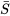 . La figure 4.2.4.4 illustre une distribution approximative pour
. La figure 4.2.4.4 illustre une distribution approximative pour 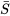 et l’aire correspondant à
et l’aire correspondant à 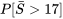 17]" title="P[\bar{S}>17]" class="latex mathjax">.
17]" title="P[\bar{S}>17]" class="latex mathjax">.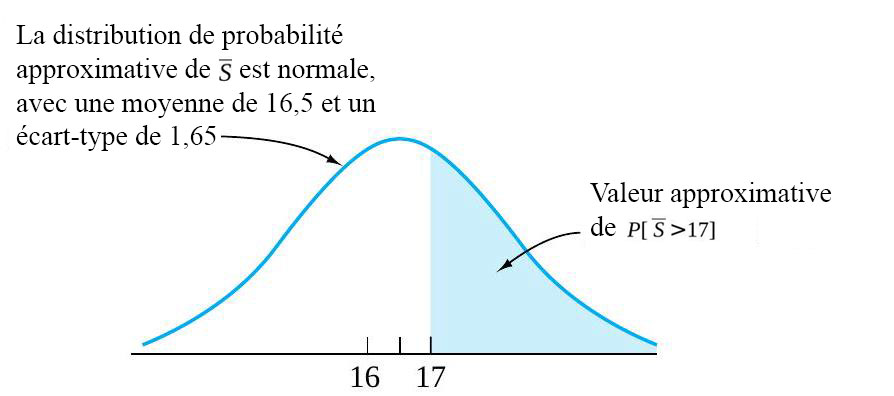
.
 avant de consulter la table normale standard. Dans ce cas, la moyenne et l’écart-type à utiliser sont (respectivement)
avant de consulter la table normale standard. Dans ce cas, la moyenne et l’écart-type à utiliser sont (respectivement)  et
et 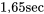 . Les cotes
. Les cotes 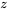 valent donc :
valent donc :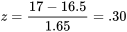
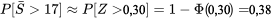 17] \approx P[Z>0,30]=1-\Phi(0,30)=0,38" title="P[\bar{S}>17] \approx P[Z>0,30]=1-\Phi(0,30)=0,38" class="latex mathjax">
17] \approx P[Z>0,30]=1-\Phi(0,30)=0,38" title="P[\bar{S}>17] \approx P[Z>0,30]=1-\Phi(0,30)=0,38" class="latex mathjax">Cote z d’une moyenne d’échantillon
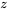 calculée dans l’exemple est une application de l’équation générale suivante :
calculée dans l’exemple est une application de l’équation générale suivante :4.2.4.1 Cote z calculée pour la moyenne d’un échantillon
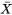 est approximativement normale si
est approximativement normale si 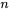 est grand, auquel cas il y a des équations pour obtenir sa moyenne et son écart-type.
est grand, auquel cas il y a des équations pour obtenir sa moyenne et son écart-type.