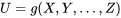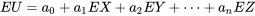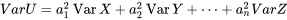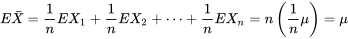4.2.3 Moyenne et variance des combinaisons linéaires de variables aléatoires

La section précédente a présenté les mathématiques utilisées pour modéliser simultanément plusieurs variables aléatoires. Une utilisation importante de ces outils en ingénierie concerne l’analyse des résultats de systèmes qui sont fonctions d’entrées aléatoires. Cette section porte sur la manière dont la variation d’une variable aléatoire de sortie dépend
des variables utilisées pour la produire. Nous nous concentrerons sur l’utilisation de combinaisons linéaires de variables aléatoires.

Distribution d’une fonction de variables aléatoires

Le problème examiné dans cette section est le suivant. Soient une distribution conjointe pour les variables aléatoires [latex]X, Y,…, Z[/latex] et une fonction 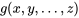g(x, y,...,z). L’objectif est de prédire le comportement de la variable aléatoire

4.2.3.1                        U=g(X, Y, \ldots, Z)

Dans certains cas très simples, il est possible de trouver exactement la distribution dont U hérite de X, Y,...,Z

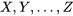
Exemple 4.2.3.1 Distribution du jeu entre deux pièces assemblées dont les dimensions sont déterminées de manière aléatoire

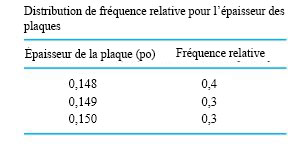
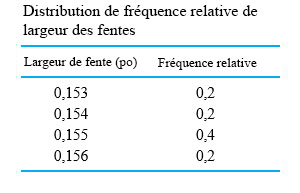
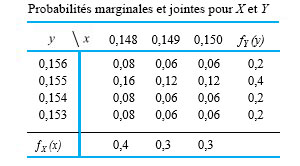
Supposons qu’une plaque d’acier d’une épaisseur nominale de 0,15 po doit reposer dans une rainure d’une largeur nominale de 0,155 po usinée sur la surface d’un bloc d’acier. Un lot de plaques a été fabriqué et les épaisseurs ont été mesurées, produisant la distribution de fréquence relative du tableau 4.2.3.1; une distribution de fréquence relative pour les largeurs de rainure mesurées sur un lot de blocs usinés est donnée dans le tableau 4.2.3.2.

Si une plaque est choisie au hasard et qu’un bloc est choisi séparément au hasard, la distribution conjointe naturelle pour les variables aléatoires

X = l’épaisseur de la plaque
Y = la largeur de la rainure

est indépendante, avec la distribution marginale de X donnée dans le tableau 4.2.3.1 et la distribution marginale de Y donnée dans le tableau 4.2.3.2. En d’autres termes, le tableau 4.2.3.3 donne une fonction de probabilité conjointe plausible pour X et Y.

 

Tableau 4.2.3.1

 

Tableau 4.2.3.2

Une variable dérivée de X et Y qui présente un intérêt potentiel substantiel est le jeu dans l’assemblage plaque/bloc,

U = Y – X

Remarquez qu’en prenant les extrêmes représentés dans les tableaux 4.2.3.1 et 4.2.3.2, U doit se trouver dans la plage comprise entre (0,153 – 0,150 =) 0,003 po et *(0,156 – 0,148 =) 0,008 po. Cependant, on peut obtenir beaucoup plus d’informations. En examinant le tableau 4.2.3.3, on constate que les diagonales des entrées (du bas à gauche au haut à droite) correspondent toutes à la même valeur de Y – X. En additionnant les probabilités sur ces diagonales, on obtient la distribution de U donnée dans le tableau 4.2.3.4.

 

Tableau 4.2.3.3

 

Tableau 4.2.3.4

L’exemple 4.2.3.1 implique une distribution conjointe discrète très simple et une fonction g très simple, à savoir, g(x, y) = y – x. En général, il n’est pas possible en pratique de trouver une solution complète et exacte pour la distribution de U = g(X, Y,…,Z ). Heureusement, pour de nombreuses applications des probabilités en ingénierie, les solutions approximatives et/ou partielles suffisent à répondre aux questions d’intérêt pratique.

Moyenne et variance d’une combinaison linéaire de variables aléatoires

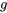Pour les besoins de l’ingénierie, il suffit souvent de connaître la moyenne et la variance de U données par l’équation 4.2.3.1. (Autrement dit, nul besoin de connaître la distribution complète de U.) Lorsque c’est le cas et que g est linéaire, il existe des formules explicites pour trouver ces valeurs.
.

PROPOSITION 4.2.3.2

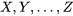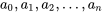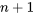Soient X, Y, \ldots, Z sont n variables aléatoires indépendantes, et a_{0}, a_1, a_2, \ldots, a_{n}, n+1 constantes. La variable aléatoire 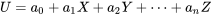U=a_{0}+a_1 X+a_2 Y+\cdots+a_{n} Z a alors une moyenne de

4.2.3.3                    E(U)=a_{0}+a_ E(X)+a_ E(Y)+\cdots+a_{n} E(Z)

et une variance de
.

4.2.3.4                    Var(U)=a_1^2 \operatorname{Var(X)} +a_2^2 \operatorname{Var(Y)} +\cdots+a_{n}^2 \operatorname{Var(Z)}

.
L’équation 4.2.3.3 est valide indépendamment du fait que les variables X, Y, \ldots, Z soient dépendantes ou indépendantes. Par contre, l’équation 4.2.3.4 repose sur l’indépendance des variables, mais il existe une façon de la généraliser aux cas où les variables sont dépendantes. Cependant, la forme de l’équation 4.2.3.4 donnée ici est adéquate pour les besoins actuels.
.
Un type d’application dans lequel la proposition 4.2.3.2 est immédiatement utile est celui des problèmes de tolérances géométriques, auquel cas on a a_{0}=0, et les autres a_{i}=\pm 1.
.

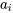Exemple 4.2.3.2 Jeu d’une plaque d’acier.

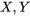Reprenons la situation du jeu nécessaire pour insérer une plaque d’acier dans une rainure usinée sur un bloc d’acier. Soient X, Y, et U l’épaisseur de la plaque, la largeur de la rainure et le jeu (respectivement). Les moyennes et variances pour ces variables peuvent alors être calculées. Nous vous invitons à vérifier que
.
\begin{array}{lll}E(X)=0,1489 & \text { et } & \operatorname{Var(X)}=6,9 \times 10^{-7} \\E(Y)=0,1546 & \text { et } & \operatorname{Var(Y)}=1,04 \times 10^{-6}\end{array}
.
Comme
.
[latex]U=Y-X=(-1) X+1 Y[/latex]
.
Il est possible d’appliquer la proposition 4.2.3.2 et de conclure que
.
\begin{aligned}E(U) & =-1 E(X)+1 E(Y)=-0,1489+0,1546=0,0057 \text{ po} \\\operatorname{Var(U)} & =(-1)^2 6,9 \times 10^{-7}+(1)^2 1,04 \times 10^{-6}=1,73 \times 10^{-6} \text{ po}^2 \end{aligned}
.
Ainsi,
.
\sqrt{\operatorname{Var(U)}}=0,0013 \text { po }
.
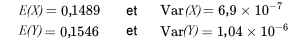
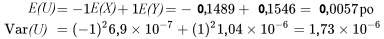
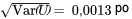
Il vaut la peine de vérifier que la moyenne et l’écart-type du jeu obtenu à l’aide de la proposition 4.2.3.2 concordent avec les valeurs obtenues à l’aide de la distribution de U figurant dans le tableau 4.2.3.4 et les formules de la moyenne et de la variance données dans la partie 3. L’avantage d’utiliser la proposition 4.2.3.2 est que si on a seulement besoin de 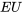E(U) et de [latex]\operatorname{Var(U)}[/latex], ce n’est pas nécessaire de passer par l’étape intermédiaire consistant à obtenir la distribution de U. Les calculs effectués à l’aide de la proposition 4.2.3.2 n’utilisent que les caractéristiques des distributions marginales.

.

Variables aléatoires 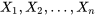X_1, X_2, \ldots, X_{n} modélisant des sélections aléatoires (avec remplacement) dans une même population

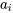Une autre utilisation particulièrement importante de la proposition 4.2.3.2 concerne n variables aléatoires iid pour lesquelles les coefficients a_{i} valent tous 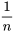\frac{ 1}{n}. Autrement dit, lorsque les variables aléatoires 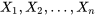X_, X_, \ldots, X_{n} sont conceptuellement équivalentes à des sélections aléatoires (avec remplacement) dans une même population, la proposition 4.2.3.2 indique comment la moyenne et la variance de la variable aléatoire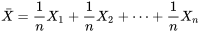
.
\bar{X}=\frac{ 1}{n} X_{ 1}+\frac{ 1}{n}X_2+\cdots+\frac{ 1}{n} X_{n}
.
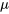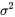sont liées aux paramètres de la population \mu et \sigma^2. Pour les variables indépendantes 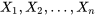X_1, X_2, \ldots, X_{n} de même moyenne 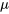\mu et de même variance 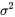\sigma^2, la proposition 4.2.3.2 énonce que :
.
4.2.3.5  Moyenne d’une moyenne de n variables aléatoires iid
.
E (\bar{X})=\frac{ 1}{n} E(X_1)+\frac{ 1}{n} E (X_2)+\cdots+\frac{ 1}{n} E (X_{n})=n\left(\frac{ 1}{n} \mu\right)=\mu
et
4.2.3.6 Variance d’une moyenne de n variables aléatoires iid
.
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/a7fa64aca13a7c86d0d0875dfb4350c6.png » alt= »\begin{aligned}\operatorname{Var( \bar{X} )} & =\left(\frac{ 1}{n}\right)^2 \operatorname{Var(X_1)} +\left(\frac{ 1}{n}\right)^2 \operatorname{Var(X_2)} +\cdots+\left(\frac{ 1}{n}\right)^2 \operatorname{Var(X_{n})} \\& =n\left(\frac{ 1}{n}\right)^2 \sigma^2=\frac{\sigma^2}{n}\end{aligned}
.
Étant donné que [latex]\sigma^2 / n[/latex] » title= »\begin{aligned}\operatorname{Var( \bar{X} )} & =\left(\frac{ 1}{n}\right)^2 \operatorname{Var(X_1)} +\left(\frac{ 1}{n}\right)^2 \operatorname{Var(X_2)} +\cdots+\left(\frac{ 1}{n}\right)^2 \operatorname{Var(X_{n})} \\& =n\left(\frac{ 1}{n}\right)^2 \sigma^2=\frac{\sigma^2}{n}\end{aligned}
.
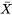Étant donné que [latex]\sigma^2 / n[/latex] » class= »latex mathjax »> diminue en \frac{ 1}{n}\frac{ 1}{n}title, les équations 4.2.3.5 et 4.2.3.6 présente l’image rassurante de \bar{X} ayant la distribution de probabilité centrée sur la moyenne de la population 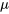\mu, avec une dispersion qui diminue au fur et à mesure que la taille de l’échantillon augmente.
.
Les relations 4.2.3.5 et 4.2.3.6, qui décrivent parfaitement le comportement aléatoire de \bar{X}[/latex] dans le cadre d’un échantillonnage aléatoire avec remplacement, sont également des descriptions approximatives du comportement de [latex][/latex]\bar{X} dans le cadre d’une échantillonnage aléatoire simple dans des contextes énumératifs. (Rappelons la discussion sur l’indépendance approximative des observations résultant d’un échantillonnage aléatoire simple dans une grande population.)

Licence

Introduction aux méthodes statistiques en ingénierie© par C. Bassim et Bryan Lee. Tous droits réservés.

Partagez ce livre