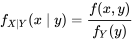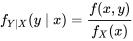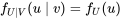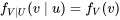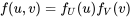4.2.2 Distributions conditionnelles et indépendance
Distributions conditionnelles et indépendance des variables aléatoires discrètes
Lorsqu’on travaille avec plusieurs variables aléatoires, il est souvent utile de réfléchir à ce que l’on attend de l’une des variables compte tenu des valeurs prises par toutes les autres. Par exemple, dans l’exercice du couple de serrage du boulon 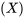 , un technicien qui vient de desserrer le boulon 3 et qui a mesuré le couple à la valeur
, un technicien qui vient de desserrer le boulon 3 et qui a mesuré le couple à la valeur 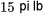 devrait avoir des attentes pour le couple du boulon 4
devrait avoir des attentes pour le couple du boulon 4 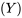 quelque peu différentes, à la lumière de la distribution marginale du tableau 4.2.1.3. Après tout, si on reprend les données du tableau 4.2.2.1, la distribution de la fréquence relative des couples des boulons 4 pour les composants dont le couple du boulon 3 est de
quelque peu différentes, à la lumière de la distribution marginale du tableau 4.2.1.3. Après tout, si on reprend les données du tableau 4.2.2.1, la distribution de la fréquence relative des couples des boulons 4 pour les composants dont le couple du boulon 3 est de 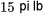 est similaire aux valeurs du tableau 4.2.2.1. D’une certaine manière, le fait de savoir que
est similaire aux valeurs du tableau 4.2.2.1. D’une certaine manière, le fait de savoir que 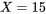 devrait modifier la distribution de probabilité de
devrait modifier la distribution de probabilité de  pour que la distribution de fréquence relative corresponde au tableau 4.2.2.1 plutôt qu’à la distribution marginale du tableau 4.1.1.3.
pour que la distribution de fréquence relative corresponde au tableau 4.2.2.1 plutôt qu’à la distribution marginale du tableau 4.1.1.3.

La théorie des probabilités tient compte de cette notion de « distribution d’une variable lorsqu’on connaît les valeurs des autres » à travers le concept de distribution conditionnelle. La version à deux variables est définie ci-après.
DÉFINITION 4.2.2.1. Fonction de probabilité conditionnelle de X étant donné que Y=y
EXPRESSION 4.2.2.1
 et
et  avec une fonction de probabilité conjointe
avec une fonction de probabilité conjointe 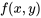 , la fonction de probabilité conditionnelle de
, la fonction de probabilité conditionnelle de  étant donné que
étant donné que 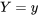 est la fonction de
est la fonction de 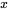 suivante :
suivante :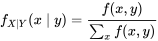
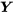 étant donné que
étant donné que 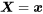 est la fonction de
est la fonction de 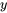 suivante :
suivante :Fonction de probabilité conditionnelle de X étant donné que Y=y 4.2.2.2
Fonction de probabilité conditionnelle pour Y étant donné que X=x 4.2.2.3
Calcul de distributions conditionnelles à partir d’une fonction de probabilité conjointe
Les équations 4.2.2.2 et 4.2.2.3 sont parfaitement logiques. La première indique qu’à partir d’une fonction 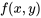 répertoriée dans un tableau à deux entrées et en ne considérant que la ligne
répertoriée dans un tableau à deux entrées et en ne considérant que la ligne 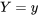 , la distribution conditionnelle appropriée pour
, la distribution conditionnelle appropriée pour  est indiquée par les probabilités de cette ligne (les valeurs de
est indiquée par les probabilités de cette ligne (les valeurs de 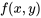 ), qu’on divise par leur somme
), qu’on divise par leur somme 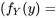
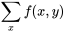 ) pour les renormaliser (faire en sorte qu’elles totalisent 1). De même, l’équation 4.2.2.3 indique que si l’on considère uniquement la colonne
) pour les renormaliser (faire en sorte qu’elles totalisent 1). De même, l’équation 4.2.2.3 indique que si l’on considère uniquement la colonne 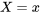 , la distribution conditionnelle appropriée pour
, la distribution conditionnelle appropriée pour  est donnée par les probabilités de cette colonne divisées par leur somme.
est donnée par les probabilités de cette colonne divisées par leur somme.
Exemple 4.2.2.1. Couples des boulons (suite)
 étant donné que
étant donné que 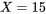 .
.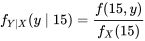
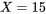 est
est 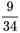 . Ainsi, en divisant les valeurs dans la colonne
. Ainsi, en divisant les valeurs dans la colonne 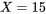 de ce tableau par
de ce tableau par 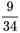 , on obtient la distribution conditionnelle pour
, on obtient la distribution conditionnelle pour  , qui est présentée dans le tableau 4.2.2.2. Si l’on compare ce résultat au tableau 4.2.1.4, on constate que l’équation 4.2.2.3 produit une distribution conditionnelle conforme à l’intuition.
, qui est présentée dans le tableau 4.2.2.2. Si l’on compare ce résultat au tableau 4.2.1.4, on constate que l’équation 4.2.2.3 produit une distribution conditionnelle conforme à l’intuition.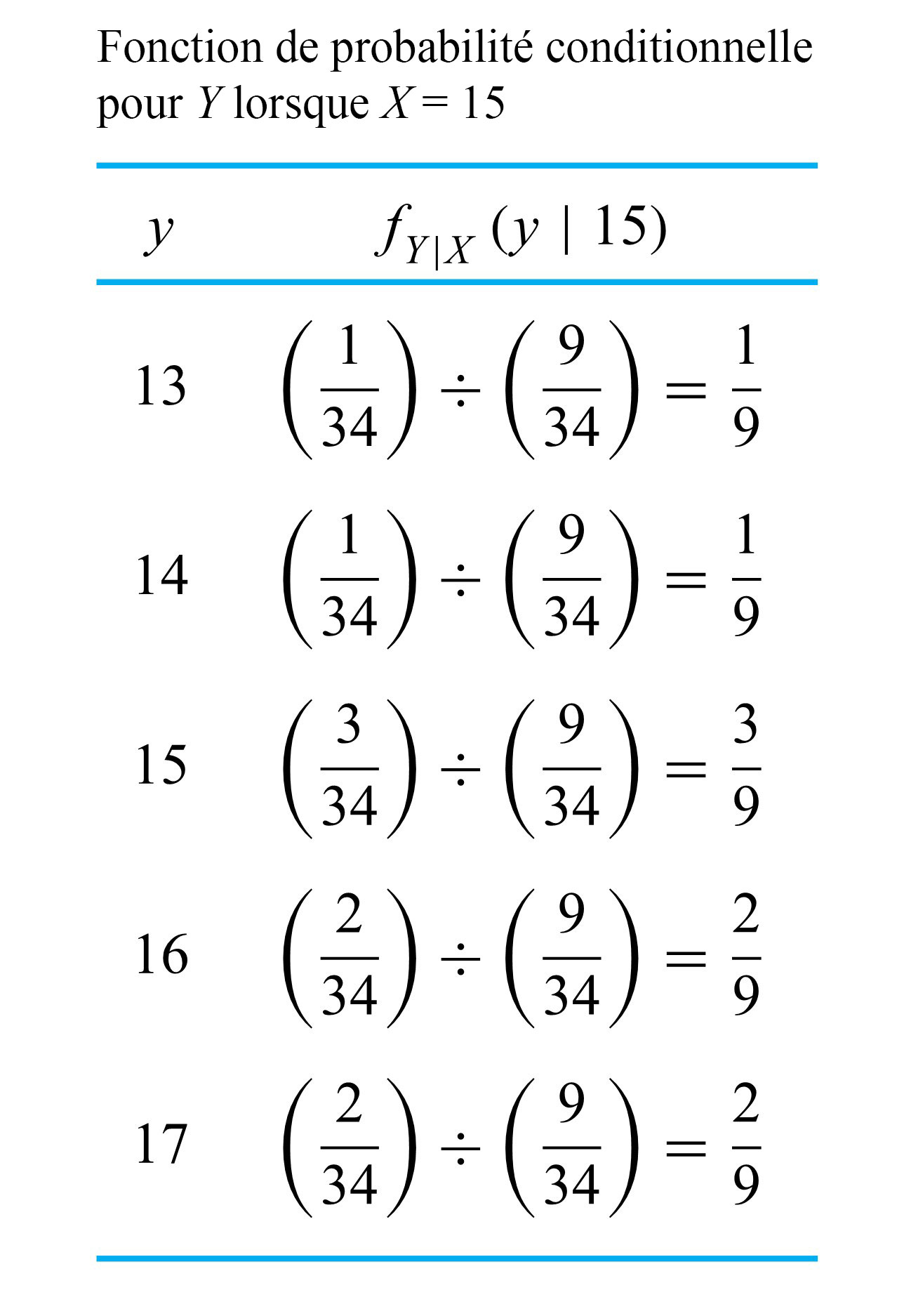
 f_{Y \mid X}(y \mid 18) :
f_{Y \mid X}(y \mid 18) :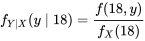
 étant donné que
étant donné que 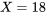 , présentée dans le tableau 4.2.2.3. Les tableaux 4.2.2.2 et 4.2.4.3 confirment que les distributions conditionnelles de
, présentée dans le tableau 4.2.2.3. Les tableaux 4.2.2.2 et 4.2.4.3 confirment que les distributions conditionnelles de  étant donné que
étant donné que 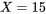 et étant donné que
et étant donné que 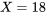 sont très différentes. Par exemple, si on sait que
sont très différentes. Par exemple, si on sait que 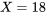 , on s’attend à ce que
, on s’attend à ce que  soit plus grand que lorsque
soit plus grand que lorsque 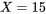 .
.
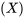 étant donné que le couple du boulon 4 est de 20
étant donné que le couple du boulon 4 est de 20 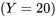 . Dans cette situation, l’équation 4.2.2.2 donne :
. Dans cette situation, l’équation 4.2.2.2 donne :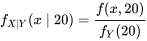
 sont les valeurs de la ligne
sont les valeurs de la ligne 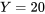 du tableau 4.2.1.2 divisées par la valeur marginale de
du tableau 4.2.1.2 divisées par la valeur marginale de 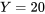 .)
.) 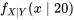 est répertoriée dans le tableau 4.2.2.4.
est répertoriée dans le tableau 4.2.2.4.
L’exemple du couple des boulons présente la particularité que les distributions conditionnelles de  étant donné les valeurs possibles pour
étant donné les valeurs possibles pour  sont différentes. En outre, ces distributions ne sont généralement pas identiques à la distribution marginale de
sont différentes. En outre, ces distributions ne sont généralement pas identiques à la distribution marginale de 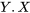 . [latex]X[/latex] fournit des informations à propos de
. [latex]X[/latex] fournit des informations à propos de  , en ce sens que selon sa valeur, il existe différentes évaluations de probabilité pour
, en ce sens que selon sa valeur, il existe différentes évaluations de probabilité pour  . Comparez cette situation à l’exemple suivant.
. Comparez cette situation à l’exemple suivant.
Exemple 4.2.2.2. Échantillonnage aléatoire de deux couples du boulon 4


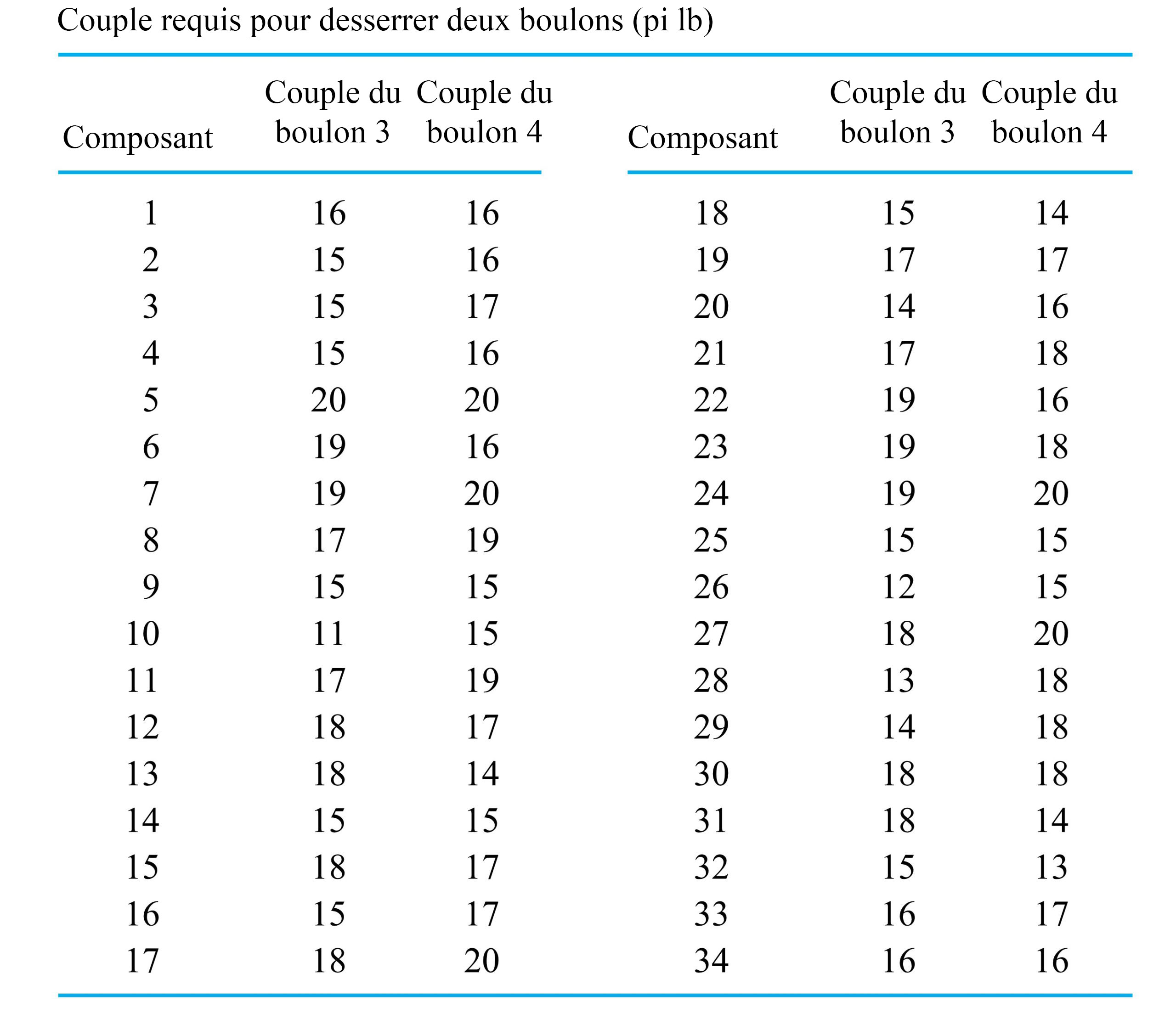
 et
et  de l’exemple 4.2.2.1, les variables
de l’exemple 4.2.2.1, les variables  et
et 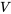 ne fournissent aucune information l’une sur l’autre. Quelle que soit la valeur de
ne fournissent aucune information l’une sur l’autre. Quelle que soit la valeur de  , la distribution de fréquence relative des couples du boulon 4 dans le chapeau est correcte comme distribution de probabilité (conditionnelle) pour
, la distribution de fréquence relative des couples du boulon 4 dans le chapeau est correcte comme distribution de probabilité (conditionnelle) pour 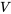 , et inversement. En d’autres termes, non seulement
, et inversement. En d’autres termes, non seulement  et
et  partagent la distribution marginale commune du tableau 4.2.2.6, mais il est également vrai que pour tout
partagent la distribution marginale commune du tableau 4.2.2.6, mais il est également vrai que pour tout 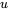 et tout
et tout 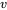 , on a :
, on a :4.2.2.4
4.2.2.5
 and
and 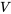 doivent être structurées, puisqu’en réécrivant le côté gauche de l’équation 4.2.2.4 à l’aide de l’expression 4.2.2.2, on obtient :
doivent être structurées, puisqu’en réécrivant le côté gauche de l’équation 4.2.2.4 à l’aide de l’expression 4.2.2.2, on obtient :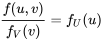
4.2.2.6
 et
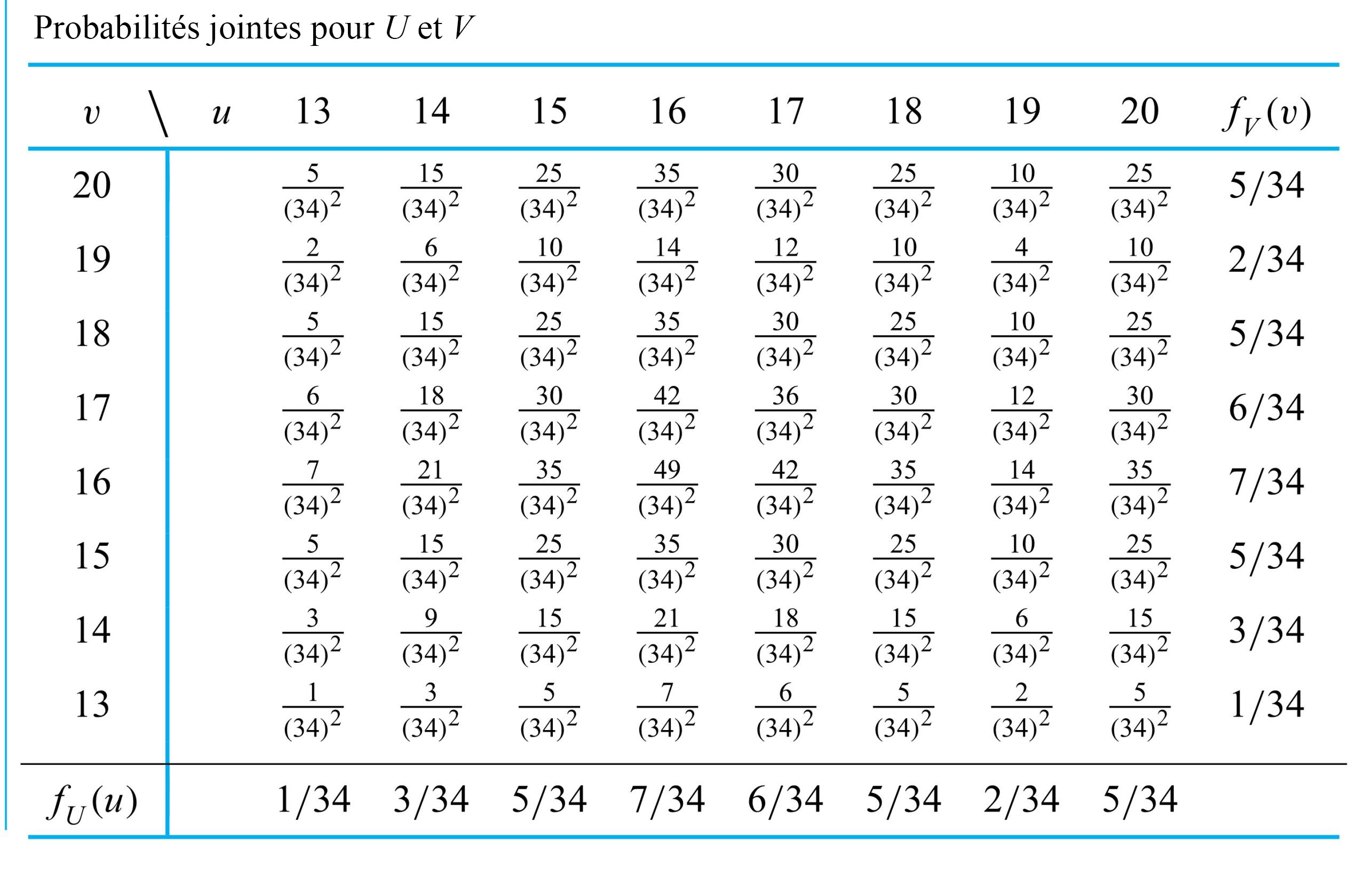
et 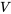 s’obtiennent en multipliant les probabilités marginales correspondantes. Le tableau 4.2.2.7 donne la fonction de probabilité conjointe pour
s’obtiennent en multipliant les probabilités marginales correspondantes. Le tableau 4.2.2.7 donne la fonction de probabilité conjointe pour  et
et 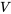 .
.
Indépendance des observations dans les études statistiques
L’exemple 4.2.2.2 suggère qu’on peut formaliser la notion intuitive que pour des variables aléatoires non liées, les distributions conditionnelles sont toutes égales aux distributions marginales correspondantes. De manière équivalente, on peut dire que les probabilités conjointes sont les produits des probabilités marginales correspondantes. Formellement, dans ce genre de cas, on parle de variables aléatoires indépendantes. La définition pour le cas à deux variables est la suivante.
DÉFINITION 4.2.2.7. Indépendance des variables aléatoires
EXPRESSION 4.2.2.7
 et
et  sont dites indépendantes si leur fonction de probabilité conjointe
sont dites indépendantes si leur fonction de probabilité conjointe 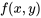 est le produit de leurs fonctions de probabilité marginales respectives. Autrement dit, l’indépendance signifie que
est le produit de leurs fonctions de probabilité marginales respectives. Autrement dit, l’indépendance signifie que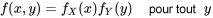
 et
et  sont dite dépendantes.
sont dite dépendantes. et
et 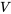 de l’exemple 4.2.2.2 sont indépendantes, tandis que les variable
de l’exemple 4.2.2.2 sont indépendantes, tandis que les variable  et
et  de l’exemple 4.2.2.1 sont dépendantes. En outre, les deux distributions conjointes illustrées à la figure 4.2.1.3 donnent un exemple de distribution conjointe fortement dépendante (la première) et de distribution conjointe indépendante (la seconde) qui ont les mêmes fonctions marginales.
de l’exemple 4.2.2.1 sont dépendantes. En outre, les deux distributions conjointes illustrées à la figure 4.2.1.3 donnent un exemple de distribution conjointe fortement dépendante (la première) et de distribution conjointe indépendante (la seconde) qui ont les mêmes fonctions marginales.Exemple 4.2.2.3. Exemple du couple des boulons (suite)
 and
and 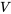 n’est pas un échantillonnage aléatoire simple. L’échantillonnage aléatoire simple tel que défini dans la partie 1 est un échantillonnage sans remplacement, et non la méthode d’échantillonnage avec remplacement utilisée pour produire
n’est pas un échantillonnage aléatoire simple. L’échantillonnage aléatoire simple tel que défini dans la partie 1 est un échantillonnage sans remplacement, et non la méthode d’échantillonnage avec remplacement utilisée pour produire  et
et 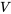 . En effet, si le premier papier n’est pas remplacé avant que le second ne soit sélectionné, les probabilités du tableau 4.2.2.7 ne décrivent pas
. En effet, si le premier papier n’est pas remplacé avant que le second ne soit sélectionné, les probabilités du tableau 4.2.2.7 ne décrivent pas  et
et 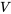 . Par exemple, si aucun remplacement n’est effectué, puisqu’un seul papier est étiqueté
. Par exemple, si aucun remplacement n’est effectué, puisqu’un seul papier est étiqueté 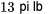 , il faut clairement que
, il faut clairement que![f(13,13)=P[U=13 \text { et } V=13]=0 f(13,13)=P[U=13 \text { et } V=13]=0](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/105fe4b3d7cbdef4eeb0ae8e8ae09cd5.png)
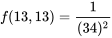
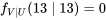
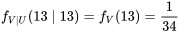
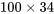 papiers, en suivant la fréquence relative du tableau 4.2.2.6. Ainsi, même si l’échantillonnage est effectué sans remplacement, les probabilités développées précédemment pour
papiers, en suivant la fréquence relative du tableau 4.2.2.6. Ainsi, même si l’échantillonnage est effectué sans remplacement, les probabilités développées précédemment pour  et
et  (et placées dans le tableau 4.2.2.7) restent aux moins approximativement valides. Par exemple, avec 3 400 papiers et en utilisant un échantillonnage sans remplacement, on a :
(et placées dans le tableau 4.2.2.7) restent aux moins approximativement valides. Par exemple, avec 3 400 papiers et en utilisant un échantillonnage sans remplacement, on a :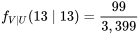
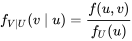
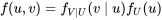
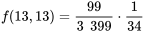
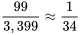
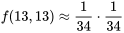
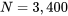 est beaucoup plus grande que la taille de l’échantillon
est beaucoup plus grande que la taille de l’échantillon 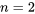 , l’indépendance est une description approximative appropriée des observations obtenues à l’aide d’un échantillonnage aléatoire simple.
, l’indépendance est une description approximative appropriée des observations obtenues à l’aide d’un échantillonnage aléatoire simple.Variables aléatoires indépendantes et identiquement distribuées
DÉFINITION 4.2.2.8. Variables indépendantes et identiquement distribuées.
Si les variables aléatoires 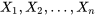 ont toutes la même distribution marginale et sont indépendantes, on dit qu’elles sont indépendantes et identiquement distribuées (iid).
ont toutes la même distribution marginale et sont indépendantes, on dit qu’elles sont indépendantes et identiquement distribuées (iid).
Par exemple, la distribution conjointe de  et
et 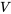 donnée dans le tableau 4.2.2.7 indique que
donnée dans le tableau 4.2.2.7 indique que  et
et 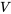 sont des variables aléatoires iid.
sont des variables aléatoires iid.
Observations pouvant être modélisées comme des variables iid