4.1.5 La règle empirique
La règle empirique
Si X est une variable aléatoire suivant une distribution normale avec une moyenne de µ et un écart-type de σ, alors la règle empirique énonce ce qui suit :
- Environ 68% des valeurs de x se situent entre –σ et +σ de la moyenne µ (à moins d’un écart-type de la moyenne).
- Environ 95% des valeurs de x se situent entre -2σ et +2σ de la moyenne µ (à moins de deux écarts-types de la moyenne).
- Environ 99,7% des valeurs de x se situent entre -3σ et +3σ de la moyenne µ (à moins de trois écarts-types de la moyenne). Autrement dit, presque toutes les valeurs x se situent à moins de trois écarts types de la moyenne.
- Les cotes z pour +σ et –σ sont +1 et -1, respectivement.
- Les cotes z pour +2σ et -2σ sont +2 et -2, respectivement.
- Les cotes z pour +3σ et -3σ sont +3 et -3, respectivement.
La règle empirique est également connue sous le nom de règle 68-95-99,7. Elle est illustrée à la figure 4.1.5.1.
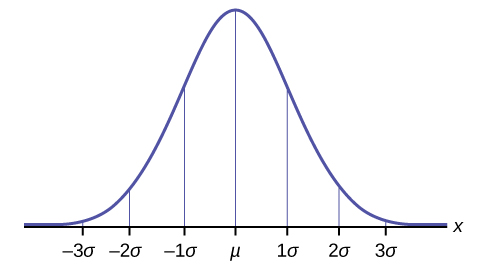
Figure 4.1.5.1. La règle empirique.
