4.1.3 Distribution normale de probabilités

Distribution normale de probabilités

Bien qu’il existe plusieurs distributions continues couramment appliquées aux problèmes d’ingénierie, la distribution normale est particulièrement importante.  De manière formelle, la distribution normale se définit comme suit :

DÉFINITION 4.1.3.1. Distribution normale

EXPRESSION 4.1.3.1

f(x)=\frac{ 1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2}

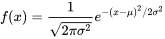
pour tout x, avec 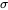\sigma > 0.

Ce n’est pas nécessairement évident, mais l’équation 4.1.3.1 donne une densité de probabilité légitime, dans la mesure où l’aire totale sous la courbe y = f(x) est égale à 1. En outre, il est également vrai que :

Moyenne et variance d’une distribution normale

E(X)=\int_{-\infty}^{\infty} x \frac{ 1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2} d x=\mu

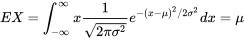
et

\operatorname{Var(X)} =\int_{-\infty}^{\infty}(x-\mu)^2 \frac{ 1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2} d x=\sigma^2

 

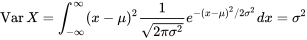
Paramètres de la distribution normale

La distribution normale a deux paramètres (deux mesures numériques descriptives de la distribution théorique), la moyenne µ et la variance 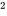\sigma^2 (on se rappelle que l’écart-type = 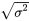\sqrt{\sigma^2} = σ).  La figure 4.1.3.1 illustre la notation de la distribution normale standard et indique que la forme de la distribution dépend de ces paramètres. Comme l’aire sous la courbe doit être égale à 1, un changement dans l’écart-type σ entraîne une modification de la forme de la courbe; la courbe devient plus large ou plus étroite selon si σ augmente ou diminue, respectivement. Une modification de μ entraîne une translation du graphique vers la gauche ou la droite. En vertu de ces deux paramètres, il existe un nombre infini de distributions de probabilités normales.

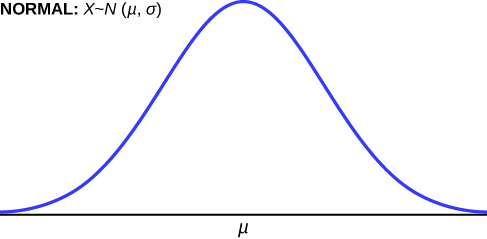
Figure 4.1.3.1. Notation de la distribution normale standard.

 

Les paramètres µ et 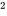\sigma^2 utilisés dans la définition 4.1.3.1 sont, respectivement, la moyenne et la variance (telles que définies dans les définitions 4.1.2.1 et 4.1.2.2) de la distribution. La figure 4.13.2 représente un graphique de la densité de probabilité donnée par l’équation 4.1.3.1. La courbe en forme de cloche représentée ici est symétrique par rapport à x = µ et présente des points d’inflexion à x = µ ± σ.

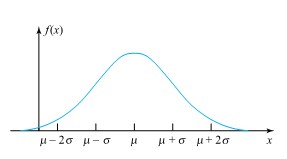
Figure 4.1.3.2. Graphique d’une fonction de densité de probabilité
normale

 

L’équation 4.1.3.1 a plusieurs origines théoriques, mais c’est également une forme qui se révèle empiriquement utile dans une grande variété d’applications. En théorie, les probabilités des distributions normales peuvent être trouvées directement par intégration en utilisant l’équation 4.1.3.1. En effet, les calculatrices de poche préprogrammées pour effectuer l’intégration numérique permettent de vérifier certains des calculs dans les exemples qui suivent, en utilisant directement les équations 4.1.1.2 et 4.1.3.1. Nous utiliserons également le calcul statistique pour les trouver à l’aide d’une formule.  Mais les méthodes d’évaluation des intégrales par primitives utilisées en première année de calcul échoueront lorsqu’il s’agira des distributions normales. Ces fonctions n’ont pas de primitives exprimables en termes de fonctions élémentaires. On utilise plutôt des tables de probabilités basées sur une version spécialisée de la distribution normale : la distribution normale réduite.

Licence

Introduction aux méthodes statistiques en ingénierie© par C. Bassim et Bryan Lee. Tous droits réservés.

Partagez ce livre