4.1.1 Fonction de densité de probabilité et fonction de probabilité cumulative
Fonction de densité de probabilité
Les méthodes utilisées pour spécifier et décrire les distributions de probabilité ont des parallèles en physique mécanique qui sont particulièrement utiles dans le cas des distributions de probabilité continues. En mécanique, les propriétés d’une distribution de masse continue sont liées à la densité (potentiellement variable) de la masse dans la région de l’espace qu’elle occupe. La quantité de masse d’une région donnée s’obtient en intégrant la densité de masse sur cette région.
En théorie des probabilités, le concept qui correspond à la densité de masse en mécanique, c’est la densité de probabilité. Pour spécifier une distribution de probabilité continue, il faut décrire « l’épaisseur » de la probabilité dans les différentes parties de l’ensemble des valeurs possibles. La définition formelle est la suivante :
DÉFINITION 4.1.1.1. Fonction de densité de probabilité (FDP)
EXPRESSION 4.1.1.1.
Une fonction de densité de probabilité pour une variable aléatoire continue X est une fonction non négative f(x) telle que :
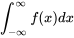
et telle que pour tout a ≤ b, P [a ≤ X ≤ b] correspond à :
EXPRESSION 4.1.1.2.
P (a ≤ X ≤ b) = 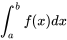
.
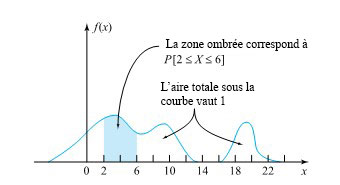
La figure 4.1.1.1 illustre une fonction de densité de probabilité (FDP) générique. Comme on peut le voir, le diagramme d’une distribution de probabilité continue est une courbe. Conformément aux équations de définition de la FDP, le graphique de f(x) ne descend pas sous l’axe des x, l’aire totale sous la courbe y = f(x) est égale à 1, et l’aire sous la courbe d’un intervalle donné correspond à la probabilité que la valeur se trouve dans cet intervalle. La fonction f(x) est définie de sorte que l’aire sous la courbe soit une probabilité. La probabilité maximale étant égale à 1, l’aire maximale est également égale à 1.
La courbe est la FDP. On utilise le symbole 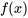 pour représenter la courbe.
pour représenter la courbe. 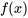 est la fonction qui correspond au graphique; on utilise la fonction de densité
est la fonction qui correspond au graphique; on utilise la fonction de densité 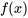 pour faire le graphique de la distribution de probabilité. L’aire sous la courbe représente la probabilité.
pour faire le graphique de la distribution de probabilité. L’aire sous la courbe représente la probabilité.
Analogie de la mécanique pour la densité de probabilité (suite)
Comme en mécanique, si f(x) est effectivement la « densité de probabilité » à x, alors la probabilité dans un petit intervalle dx autour de x est approximativement f(x) dx. (En mécanique, si f(x) est la densité de masse à x , alors la masse dans un petit intervalle dx autour de x est approximativement f(x) dx.) Pour calculer la probabilité entre a et b, il faut donc additionner les valeurs de f(x) dx. 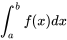 est exactement la limite de
est exactement la limite de 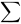 f(x) dx lorsque dx tend vers zéro. (En mécanique,
f(x) dx lorsque dx tend vers zéro. (En mécanique, 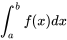 est la masse entre a et b.) L’expression dans la définition de la FDP et l’expression 4.1.1.2 sont donc raisonnables.
est la masse entre a et b.) L’expression dans la définition de la FDP et l’expression 4.1.1.2 sont donc raisonnables.
Pour une variable aléatoire continue X, P(X = a) = 0
Il y a un détail concernant les distributions de probabilité continuées qui peut sembler contre-intuitif à première vue : la probabilité qu’une variable aléatoire continue prenne une valeur précise (par exemple, a). Tout comme la masse en un seul point d’une distribution de masse continue est nulle, P(X = a) = 0 pour une variable aléatoire continue X. Cela découle de l’expression 4.1.1.2, car :
P(a 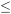 X
X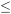 b) =
b) = 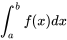 = 0
= 0
Une conséquence de cette curiosité mathématique est que lorsque l’on travaille avec des variables aléatoires continues, il n’est pas nécessaire de se préoccuper de savoir si les signes d’inégalité que l’on écrit sont des signes d’inégalité stricts. Autrement dit, si X est continue :
P(a 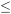 X
X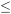 b) = P(a < X
b) = P(a < X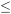 b) = P(a
b) = P(a 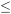 X < b) = P(a < X < b)
X < b) = P(a < X < b)
Fonction de distribution cumulative
Précédemment, nous avons donné une définition parfaitement générale de la fonction de distribution cumulative d’une variable aléatoire, et nous l’avons précisée dans le contexte des variables discrètes. On peut maintenant utiliser l’équation 4.1.1.2 pour exprimer la fonction de distribution cumulative d’une variable aléatoire continue en termes d’une intégrale de sa densité de probabilité. Soit X une variable aléatoire continue de densité de probabilité f(x) :
DÉFINITION 4.1.1.3. Fonction de distribution cumulative (FDC) d’une variable continue X
EXPRESSION 4.1.1.3
F(x) = P(X 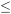 x) =
x) = 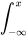 f(t) dt
f(t) dt
F(x) est calculée à partir de l’intégrale de f(x), en appliquant le théorème fondamentale du calcul à l’équation 4.1.1.3.
Autre relation entre F(x) et f(x)
EXPRESSION 4.1.1.4
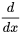 F(x) = f(x)
F(x) = f(x)
Autrement dit, f(x) est calculé à partir de la dérivée de F(x).
L’aire sous la courbe de la FDP est donnée par la FDC – ces deux fonctions ne sont pas identiques. La FDC est utilisée pour évaluer les probabilités et peut être trouvée en utilisant la géométrie, des formules, la technologie statistique ou des tables de probabilité.
Distributions de probabilités continues
Il existe de nombreuses distributions de probabilités continues. Lorsqu’on utilise une distribution de probabilité continue pour modéliser la probabilité, il faut choisir la distribution la plus adaptée au contexte. Dans ce module, nous étudierons la distribution uniforme, la distribution exponentielle et la distribution de Weibull, puis nous nous concentrerons sur la distribution la plus importante pour un cours d’introduction aux statistiques : la distribution normale.
Propriétés des distributions continues
La fonction de densité de probabilité (FDP) est utilisée pour décrire les probabilités des variables aléatoires continues. L’aire sous la courbe de densité entre deux points correspond à la probabilité que la variable se situe entre ces deux valeurs. En d’autres termes, l’aire sous la courbe entre les points a et b est égale à P(a<x<b). La fonction de distribution cumulative (FDC) donne la probabilité sous la forme d’une aire. Si X est une variable aléatoire continue, la fonction de densité de probabilité (FDP) f(x) permet de dessiner le graphique de la distribution de probabilité. L’aire totale sous le graphique de f(x) est égale à 1. L’aire sous le graphique de f(x) et entre les valeurs a et b donne la probabilité P(a<x<b). Ceci est illustré à la figure 4.1.1.2.
.
La fonction de distribution cumulative (FDC) de X est définie par P(X ≤ x). C’est une fonction de x qui donne la probabilité que la variable aléatoire est inférieure ou égale à x.
- Les résultats sont mesurés et non comptés.
- L’aire sous la courbe est égale à 1.
- La probabilité est calculée pour des intervalles de valeurs
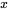 plutôt que pour des valeurs individuelles
plutôt que pour des valeurs individuelles 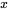 .
. - P(c<x<d) est la probabilité que la variable aléatoire
 se trouve dans l’intervalle entre les valeurs
se trouve dans l’intervalle entre les valeurs  et
et 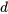 . P(c<x<d) est l’aire sous la courbe, entre
. P(c<x<d) est l’aire sous la courbe, entre  et
et 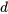 .
. 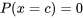 . La probabilité que
. La probabilité que 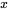 prenne une valeur précise est nulle. L’aire sous la courbe entre
prenne une valeur précise est nulle. L’aire sous la courbe entre 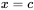 et
et 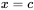 a une largeur nulle et est donc nulle.
a une largeur nulle et est donc nulle.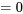 La probabilité étant égale à l’aire, la probabilité est donc également nulle.
La probabilité étant égale à l’aire, la probabilité est donc également nulle.- P(c<x<d) est égale à
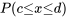 , car la probabilité est égale à l’aire.
, car la probabilité est égale à l’aire.

