3.2.6 Distribution de Poisson
Il est souvent important de noter le nombre total d’occurrences d’un phénomène relativement rare dans un intervalle de temps ou d’espace où il peut y avoir plusieurs occurrences. Par exemple, une caisse de tuiles de sol peut présenter un grand nombre d’imperfections; dans un intervalle d’une seconde, il y a potentiellement un grand nombre de messages qui peuvent arriver dans un centre de référence en vue d’être réacheminés; un échantillon de verre de 1 cc contient potentiellement un grand nombre d’imperfections.
Il faut donc des distributions de probabilités pour décrire le décompte aléatoire du nombre d’occurrences d’un phénomène relativement rare dans un intervalle de temps ou d’espace donné. Dans ce genre de situation, la distribution théorique la plus fréquemment utilisée est de loin la distribution de Poisson.
DÉFINITION 3.2.6.1. Distribution de Poisson 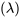
La distribution de Poisson 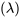 est une distribution de probabilité discrète avec la fonction de probabilité
est une distribution de probabilité discrète avec la fonction de probabilité
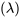 est une distribution de probabilité discrète avec la fonction de probabilité
est une distribution de probabilité discrète avec la fonction de probabilité
où 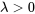 0″ title= »\lambda>0″ class= »latex mathjax »>.
0″ title= »\lambda>0″ class= »latex mathjax »>.
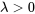 0″ title= »\lambda>0″ class= »latex mathjax »>.
0″ title= »\lambda>0″ class= »latex mathjax »>.La forme de l’équation 3.2.6.1 peut sembler un peu rébarbative au premier abord, mais il s’agit d’un modèle qui a des origines mathématiques raisonnables, qui est gérable et qui s’est révélé empiriquement utile dans de nombreux contextes d’« événements rares ». Une façon d’arriver à l’équation (3.2.6.1) est de penser à un très grand nombre d’essais indépendants (possibilités d’occurrence), où la probabilité de succès (occurrence) lors d’un seul essai est très faible et où le produit du nombre d’essais et de la probabilité de succès est 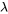 . On obtient alors la distribution binomiale
. On obtient alors la distribution binomiale 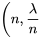 . En fait, si
. En fait, si  est grand, la fonction de probabilité binomiale
est grand, la fonction de probabilité binomiale 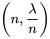 se rapproche de celle donnée dans la définition 3.2.6.1. On peut donc considérer que la distribution de Poisson pour les dénombrements résulte d’un mécanisme qui présente de nombreuses possibilités d’occurrences (à très faible probabilité) ou de non-occurrences indépendantes dans un intervalle de temps ou d’espace donné.
se rapproche de celle donnée dans la définition 3.2.6.1. On peut donc considérer que la distribution de Poisson pour les dénombrements résulte d’un mécanisme qui présente de nombreuses possibilités d’occurrences (à très faible probabilité) ou de non-occurrences indépendantes dans un intervalle de temps ou d’espace donné.
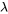 . On obtient alors la distribution binomiale
. On obtient alors la distribution binomiale 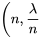 . En fait, si
. En fait, si  est grand, la fonction de probabilité binomiale
est grand, la fonction de probabilité binomiale 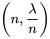 se rapproche de celle donnée dans la définition 3.2.6.1. On peut donc considérer que la distribution de Poisson pour les dénombrements résulte d’un mécanisme qui présente de nombreuses possibilités d’occurrences (à très faible probabilité) ou de non-occurrences indépendantes dans un intervalle de temps ou d’espace donné.
se rapproche de celle donnée dans la définition 3.2.6.1. On peut donc considérer que la distribution de Poisson pour les dénombrements résulte d’un mécanisme qui présente de nombreuses possibilités d’occurrences (à très faible probabilité) ou de non-occurrences indépendantes dans un intervalle de temps ou d’espace donné.La distribution de Poisson est asymétrique à droite avec 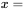
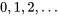 , et l’histogramme de probabilité atteint un sommet près de
, et l’histogramme de probabilité atteint un sommet près de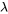 . La figure 3.2.6.1 présente deux histogrammes de probabilité de Poisson différents.
. La figure 3.2.6.1 présente deux histogrammes de probabilité de Poisson différents.
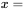
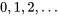 , et l’histogramme de probabilité atteint un sommet près de
, et l’histogramme de probabilité atteint un sommet près de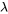 . La figure 3.2.6.1 présente deux histogrammes de probabilité de Poisson différents.
. La figure 3.2.6.1 présente deux histogrammes de probabilité de Poisson différents.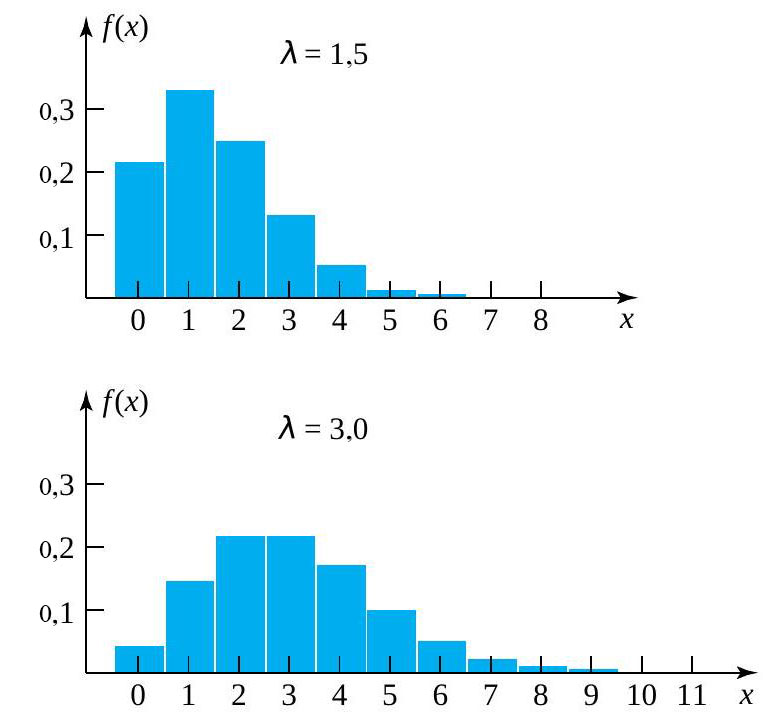
Figure 2.3.6.1. Deux histogrammes de probabilité de Poisson.
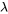 est à la fois la moyenne et la variance de la distribution de Poisson
est à la fois la moyenne et la variance de la distribution de Poisson 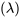 . Autrement dit, si
. Autrement dit, si  suit une distribution de Poisson
suit une distribution de Poisson 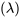 , alors
, alors
DÉFINITION 3.2.6.2. Moyenne de la distribution de Poisson 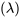
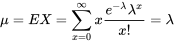
et
DÉFINITION 3.2.6.3. Variance de la distribution de Poisson 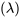
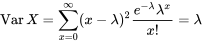
La définition 3.2.6.2 est utile pour déterminer quelle distribution de Poisson pourrait être utile pour décrire une situation d’« événements rares » donnée.
Exemple 3.2.6.1. Distribution de Poisson et décomptes de particules 
En 1910, Rutherford et Geiger ont publié dans le Philosophical Magazine un célèbre ensemble de données décrivant le nombre de particules  émises par une petite barre de polonium et entrant en collision avec un écran placé près de la barre au cours de 2 608 périodes de 8 minutes chacune. La distribution des fréquences relatives de Rutherford et Geiger a une moyenne de 3,87 et une forme remarquablement similaire à celle de la distribution de probabilité de Poisson avec une moyenne de
émises par une petite barre de polonium et entrant en collision avec un écran placé près de la barre au cours de 2 608 périodes de 8 minutes chacune. La distribution des fréquences relatives de Rutherford et Geiger a une moyenne de 3,87 et une forme remarquablement similaire à celle de la distribution de probabilité de Poisson avec une moyenne de 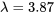 .
.
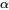 émises par une petite barre de polonium et entrant en collision avec un écran placé près de la barre au cours de 2 608 périodes de 8 minutes chacune. La distribution des fréquences relatives de Rutherford et Geiger a une moyenne de 3,87 et une forme remarquablement similaire à celle de la distribution de probabilité de Poisson avec une moyenne de
émises par une petite barre de polonium et entrant en collision avec un écran placé près de la barre au cours de 2 608 périodes de 8 minutes chacune. La distribution des fréquences relatives de Rutherford et Geiger a une moyenne de 3,87 et une forme remarquablement similaire à celle de la distribution de probabilité de Poisson avec une moyenne de 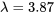 .
.Si on reproduit l’expérience de Rutherford/Geiger, on peu raisonnablement décrire

par la fonction de probabilité
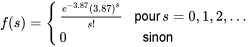
En utilisant un tel modèle, on obtient (par exemple)
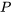 [au moins 4 particules sont enregistrées]
[au moins 4 particules sont enregistrées]![=P[S \geq 4] =P[S \geq 4]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/32e72bc46069c5e865b1358f0cb30ac6.png)
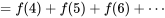
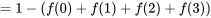
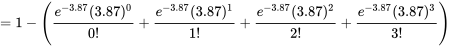
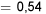
Exemple 3.2.6.2. Entrées dans la bibliothèque de l’université
Stork, Wohlsdorf et McArthur ont recueilli des données sur le nombre d’étudiant.e.s entrant dans la bibliothèque de l’ISU à différentes périodes au cours d’une semaine. Leurs données indiquent qu’entre 12 h 00 et 12 h 10 du lundi au mercredi, une moyenne d’environ 125 étudiant.e.s sont entré.e.s. Soit

Si on utilise une distribution de Poisson pour décrire 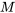 ,
, 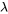 semble être
semble être
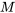 ,
, 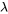 semble être
semble être
Ainsi,
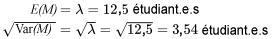
La probabilité que, par exemple, entre 10 et 15 étudiant.e.s (inclusivement) arrivent à la bibliothèque entre 12 h 00 et 12 h 01 serait évaluée comme suit :
![\begin{aligned}P[10 \leq M \leq 15]= & f(10)+f(11)+f(12)+f(13)+f(14)+f(15) \\= & \frac{e^{-12,5}(12,5)^}{10 !}+\frac{e^{-12,5}(12,5)^}{11 !}+\frac{e^{-12,5}(12,5)^}{12 !} \\& +\frac{e^{-12,5}(12,5)^}{13 !}+\frac{e^{-12,5}(12,5)^}{14 !}+\frac{e^{-12,5}(12,5)^}{15 !} \\= & .60\end{aligned} \begin{aligned}P[10 \leq M \leq 15]= & f(10)+f(11)+f(12)+f(13)+f(14)+f(15) \\= & \frac{e^{-12,5}(12,5)^}{10 !}+\frac{e^{-12,5}(12,5)^}{11 !}+\frac{e^{-12,5}(12,5)^}{12 !} \\& +\frac{e^{-12,5}(12,5)^}{13 !}+\frac{e^{-12,5}(12,5)^}{14 !}+\frac{e^{-12,5}(12,5)^}{15 !} \\= & .60\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/0fb614c04715fc8cdf4a57a37d5d8dc9.png)
