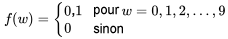3.2.1 Fonction de masse de probabilité d’une variable aléatoire discrète
Variable aléatoire discrète
Revoyons la définition d’une variable aléatoire discrète vue au module précédent :
Une variable aléatoire discrète est une variable qui ne peut prendre que certaines valeurs isolées (plutôt qu’un continuum de valeurs).
En outre, une variable aléatoire est imprévisible, et sa valeur n’est pas connue avant une expérience aléatoire. Par conséquent, décrire ou modéliser la variable aléatoire consiste à énumérer toutes les valeurs potentielles et les probabilités qui leur sont associées.
DÉFINITION 3.2.1.1. Distribution de probabilité
La spécification d’une distribution de probabilités d’une variable aléatoire consiste à donner l’ensemble des valeurs possibles et à, d’une manière ou d’une autre, attribuer de manière cohérente des chiffres compris entre 0 et 1 – appelés probabilités – qui correspondent à la probabilité que
telle ou telle valeur se réalise.
L’outil le plus souvent utilisé pour décrire une distribution de probabilité discrète est la fonction de masse de probabilité.
DÉFINITION 3.2.1.2. Fonction de masse de probabilité
La fonction de probabilité d’une variable aléatoire discrète X pouvant prendre les valeurs 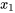 ,
,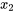 ,…, est une fonction non-négative f(x) telle que f (
,…, est une fonction non-négative f(x) telle que f (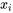 ) donne la probabilité que X prenne la valeur
) donne la probabilité que X prenne la valeur 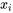 .
.
Rappel : P(X) ou P[X] signifie « la probabilité de [l’expression ou la phrase X] ». Par conséquent, la fonction de probabilité (fonction de masse de probabilité) de X est la fonction f telle que :
f(x) = P[X = x]
Autrement dit, « f(x) est la probabilité que (la variable aléatoire) X prenne la valeur x. »
Exemple 3.2.1.1. Retour sur le couple des boulons
Variable aléatoire de l’exigence de couple
Reprenons l’exemple du chapitre 2, où Brenny, Christensen et Schneider ont mesuré le couples des boulons de la plaque avant d’un composant d’équipement lourd.
Soit 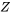 le prochain couple mesuré pour le boulon 3 (arrondi à l’entier le plus proche), que nous traiterons comme une variable aléatoire discrète. Il faut maintenant trouver une fonction de probabilité plausible pour Z. Les fréquences relatives des mesures de couple enregistrées sur le boulon 3 permettent d’établir la distribution des fréquences relative :
le prochain couple mesuré pour le boulon 3 (arrondi à l’entier le plus proche), que nous traiterons comme une variable aléatoire discrète. Il faut maintenant trouver une fonction de probabilité plausible pour Z. Les fréquences relatives des mesures de couple enregistrées sur le boulon 3 permettent d’établir la distribution des fréquences relative :
Ce tableau montre, par exemple, que pendant la période de collecte des données, environ 15 % des couples mesurés étaient de 19 pi lb. S’il est raisonnable de croire que le système qui a produit les données de ce tableau produira le couple du prochain boulon 3, il est alors logique d’établir la fonction de probabilité de Z selon les fréquences relatives de ce tableau.
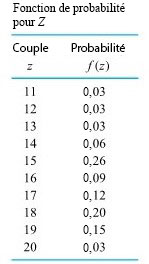
Autrement dit, on peut utiliser la distribution de probabilité spécifiée dans le prochain tableau. (En passant des fréquences relatives du premier tableau aux valeurs proposées pour f(z) dans le second tableau, les chiffres ont été arrondis de manière légèrement arbitraire pour que les valeurs de probabilité soient exprimées avec deux décimales et que leur total soit d’exactement 1,00.)
Distribution de masse de probabilité d’une valeur donnée sélectionnée aléatoirement dans une population
L’adéquation de la fonction de probabilité du tableau ci-dessus pour décrire Z dépend essentiellement de la stabilité physique du processus de serrage des boulons. Mais il y a une deuxième façon dont les fréquences relatives peuvent devenir des choix évidents pour les probabilités. Par exemple, considérons les 34 couples du tableau 3.2.1.1 comme une population, dans laquelle n = 1 élément doit être échantillonné de manière aléatoire, et soit  la valeur de couple sélectionnée.
la valeur de couple sélectionnée.
Dans ce cas, la fonction de probabilité du tableau 3.2.1.2 est également approximativement appropriée pour Y. Ce point n’est pas aussi important dans cet exemple spécifique qu’il l’est en général : lorsqu’il faut choisir une valeur hasard dans une population, une distribution de probabilité appropriée est une distribution équivalente à la distribution de fréquence relative de la population.
Principaux points à retenir
La distribution de probabilité d’une variable aléatoire répertorie toutes les valeurs possible de la variable aléatoire et la probabilité que la variable prenne chaque valeur. Elle décrit la manière dont les probabilités sont distribuées sur les valeurs de la variable aléatoire. S’il faut choisir une valeur au hasard dans une population, une distribution de probabilité appropriée est une distribution équivalente à la distribution de fréquence relative de la population.
Propriétés des fonctions de probabilité mathématiquement valides
La fonction de probabilité présentée dans le tableau 3.2.1.2 possède deux propriétés nécessaires à la cohérence mathématique d’une distribution de probabilité discrète. Les valeurs de f(z) sont toutes comprises dans l’intervalle [0, 1], et leur somme est égale à 1. Les probabilités négatives ou supérieures à 1 n’auraient aucun sens, étant donné qu’une probabilité de 1 indique une certitude d’occurrence, et une probabilité de 0 indique une impossibilité. Ainsi, selon le modèle du tableau 3.2.1.2, puisque la somme des valeurs de f(z) est égale à 1, l’occurrence de l’une des valeurs {11, 12, 13, 14, 15, 16, 17, 18, 19, 20} ft lb est certaine.
Une fonction de probabilité f(x) donne la probabilité d’occurrence de chacune des valeurs. Si on veut trouver la probabilité que X prenne n’importe laquelle des valeurs dans un sous-ensemble de ses valeurs possibles, on additionne les probabilités des valeurs du sous-ensemble.
Exemple 3.2.1.2. Retour sur le couple des boulons (suite)
Reprenons la fonction f(z) définie dans le tableau 3.2.1.2 pour trouver
P[Z > 17] = P [le couple suivant dépasse 17]
La somme des entrées de f (z) correspondant aux valeurs possibles supérieures à 17 ft lb donne
P[Z > 17] = f(18) + f(19) + f(20) = 0,20 + 0,15 + 0,03 = 0,38
La probabilité que le couple suivant soit supérieur à 17 ft lb est d’environ 38%.
Si, par exemple, les spécifications indiquent que le couple doit être compris entre 16 et 21 ft lb, la probabilité que le prochain couple mesuré soit conforme est :
P[16 ≤ Z ≤ 21] = f(16) + f(17) + f(18) + f(19) + f(20) + f(21)
= 0,09 + 0,12 + 0,20 + 0,15 + 0,03 + 0,00
= 0,59
Dans l’exemple de la mesure du couple, la fonction de probabilité est donnée sous forme de tableau. Dans d’autres cas, il est possible de trouver une équation pour f(x).
Exemple 3.2.1.3. Numéro de série d’outil aléatoire
La dernière étape du processus d’assemblage des outils pneumatiques étudié par Kraber, Rucker et Williams consistait à apposer une plaque de numéro de série sur l’outil terminé. Imaginez que vous vous rendiez à la fin de la chaîne de montage à 9 h 00 lundi prochain et que vous observiez le premier numéro de série apposé après 9 h 00.
Soit
W = le dernier chiffre du numéro de série observé
Supposons que les numéros de série des outils commencent par un code spécifique au modèle d’outil et se terminent par des numéros consécutifs reflétant le nombre d’outils du modèle en question qui ont été produits. La symétrie de cette situation suggère que les valeurs de W (w = 0, 1,…,9) sont équiprobables. Autrement dit, une fonction de probabilité plausible pour W prend la forme suivante :