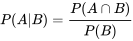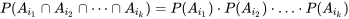3.1.2 Probabilité et indépendance des événements
Probabilité d’événements aléatoires
L’objectif de la théorie des probabilité est d’attribuer un nombre entre 0 et 1 pour mesurer la probabilité d’un événement aléatoire. Par exemple, si l’expérience consiste à tirer à pile ou face, on peut considérer l’événement 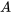 comme le fait d’obtenir au maximum une fois face. La probabilité de l’événement
comme le fait d’obtenir au maximum une fois face. La probabilité de l’événement 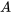 s’écrit
s’écrit 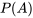 et correspond à un nombre compris entre zéro et un (inclusivement) qui décrit la proportion de fois où l’on s’attend à ce que l’événement se produise sur le long terme. P(A) = 0 signifie que l’événement A ne peut jamais se produire. P(A) = 1 signifie que l’événement A se produit toujours. P(A) = 0.5 signifie que l’événement A a la même probabilité de se produire ou de ne pas se produire. Par exemple, si vous tirez à pile ou face de manière répétée (20, 2 000 ou 20 000 fois), la fréquence relative de faces tends vers 0,5 (soit la probabilité d’obtenir face).
et correspond à un nombre compris entre zéro et un (inclusivement) qui décrit la proportion de fois où l’on s’attend à ce que l’événement se produise sur le long terme. P(A) = 0 signifie que l’événement A ne peut jamais se produire. P(A) = 1 signifie que l’événement A se produit toujours. P(A) = 0.5 signifie que l’événement A a la même probabilité de se produire ou de ne pas se produire. Par exemple, si vous tirez à pile ou face de manière répétée (20, 2 000 ou 20 000 fois), la fréquence relative de faces tends vers 0,5 (soit la probabilité d’obtenir face).
Passons en revue les axiomes de probabilité qui serviront à construire les règles de probabilité que nous utiliserons dans ce cours :
Un système de probabilités est une affectation de nombres (probabilités) 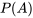 , à des événements
, à des événements 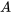 de telle sorte que :
de telle sorte que :
- Pour chaque événement
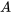 ,
, 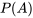 est un nombre réel non négatif compris entre 0 et 1 inclusivement. Autrement dit, 0 ≤ P(A) ≤ 1.
est un nombre réel non négatif compris entre 0 et 1 inclusivement. Autrement dit, 0 ≤ P(A) ≤ 1. - La probabilité de l’espace échantillon
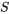 est de 1 et la probabilité de l’ensemble vide est de 0. Autrement dit, P(S) = 1 et P(∅) = 0.
est de 1 et la probabilité de l’ensemble vide est de 0. Autrement dit, P(S) = 1 et P(∅) = 0. - Les probabilités sont dénombrablement additives pour des événements disjoints. Autrement dit,
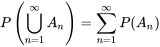
Probabilité conditionnelle et indépendance des événements
L’idée d’attribuer des probabilités à un événement en fonction de la valeur d’un autre événement est un concept essentiel pour comprendre pour les statistiques. Attribution conditionnelle de probabilités d’événements :
Pour l’événement A et l’événement B, si l’événement B a une probabilité non nulle, la probabilité conditionnelle de A étant donné B est
« 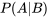 » signifie « probabilité de A, étant donné B ».
» signifie « probabilité de A, étant donné B ».
Souvent, l’événement A et l’événement B sont dépendants, ce qui veut dire que les probabilités conditionnelles s’appliquent et que les valeurs numériques de P(A|B) et P(A) sont différentes. Concrètement, cela signifie qu’on peut changer la probabilité de A si on sait que B s’est produit. Dans les cas où il n’y a pas de différence, on parle d’indépendance.
Deux événements 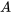 et
et 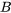 sont indépendants si le fait de savoir que l’un s’est produit n’affecte pas les chances que l’autre se produise. Par exemple, les résultats de deux lancers d’un dé standard sont des événements indépendants. Le résultat du premier jet ne modifie pas la probabilité du résultat du deuxième jet. Deux événements sont indépendants si l’un des éléments suivants est vrai :
sont indépendants si le fait de savoir que l’un s’est produit n’affecte pas les chances que l’autre se produise. Par exemple, les résultats de deux lancers d’un dé standard sont des événements indépendants. Le résultat du premier jet ne modifie pas la probabilité du résultat du deuxième jet. Deux événements sont indépendants si l’un des éléments suivants est vrai :
sont des événements avec une probabilité non-nulle dans l’espace échantillon S, et qu’ils sont indépendants, les identités suivantes s’appliquent :
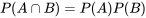 .
.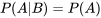 .
.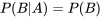 .
.
Les probabilités des événements obéissent à des règles qui découlent de l’application des axiomes des probabilités et de l’application de l’indépendance, et peuvent être illustrées comme suit :
Pour 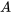 et
et 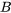 des événements dans un espace échantillon
des événements dans un espace échantillon 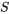 :
:
- Pour tout événement
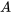 , P( A) = 1 − P(
, P( A) = 1 − P(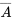 ).
). - La règle additive énonce que pour toute paire d’événements A et B : P (A ou B) = P (A) + P(B) − P(A et B)
- Pour des événements disjoints (mutuellement exclusifs) A et B, la règle additive se simplifie : P(A ou B) = P(A) + P(B)
- La règle de multiplication énonce que pour P(B) > 0, P(A et B) = P(A | B) · P(B).
- Pour des événements indépendants A et B, la règle de multiplication se simplifie : P(A et B) = P(A) · P(B).
On peut maintenant étendre la définition de l’indépendance à l’indépendance mutuelle de plusieurs événements. L’indépendance de plus de deux événements élargit la notion d’indépendance : le fait de savoir quelque chose sur certains de ces événements ne donne aucune information probabiliste sur les autres. L’indépendance mutuelle s’étend à toutes les collections d’événements dans l’espace échantillon. La notion d’indépendance mutuelle sera très importante pour l’attribution de probabilités aux événements des expériences aléatoires.
Les événements  sont mutuellement indépendants si pour tout sous-ensemble
sont mutuellement indépendants si pour tout sous-ensemble  :
:
Échantillonnage aléatoire et indépendance
L’échantillonnage peut être effectué avec remplacement ou sans remplacement.
- Avec remplacement : Chaque membre d’une population est remplacé après avoir été sélectionné, et il a la possibilité d’être sélectionné plus d’une fois. Lorsque l’échantillonnage est effectué avec remplacement, les événements sont considérés comme indépendants, ce qui signifie que le résultat de la première sélection ne modifiera pas les probabilités de la deuxième sélection.
- Sans remplacement : Lorsque l’échantillonnage est effectué sans remplacement, chaque membre d’une population ne peut être sélectionné qu’une seule fois. Dans ce cas, les probabilités de la deuxième sélection sont affectées par le résultat de la première sélection. Les événements sont considérés comme dépendants (ou non indépendants).
3.1.2.1. Échantillonnage à partir d’un jeu de cartes bien mélangé
Soit un jeu de 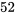 cartes bien mélangées. Il se compose de quatre couleurs : le trèfle, le carreau, le cœur et le pique. Chaque couleur comporte
cartes bien mélangées. Il se compose de quatre couleurs : le trèfle, le carreau, le cœur et le pique. Chaque couleur comporte 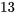 cartes :
cartes :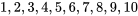 ,
, 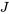 (valet),
(valet), 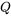 (dame),
(dame), 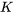 (roi) de cette couleur.
(roi) de cette couleur.
- Échantillonnage avec remplacement :Supposons qu’on sélectionne trois cartes avec remplacement. La première carte choisie sur les
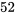 cartes est la
cartes est la 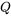 de pique. On remet la carte, on mélange le paquet et on pige une deuxième carte du jeu de
de pique. On remet la carte, on mélange le paquet et on pige une deuxième carte du jeu de 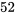 cartes. Il s’agit du 10 de trèfle. On remet la carte, on mélange le paquet et on pige une troisième carte du jeu de
cartes. Il s’agit du 10 de trèfle. On remet la carte, on mélange le paquet et on pige une troisième carte du jeu de 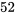 cartes. Cette fois, la carte est à nouveau la
cartes. Cette fois, la carte est à nouveau la 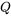 de pique. Les sélections sont {
de pique. Les sélections sont {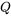 de pique, 10 de trèfle,
de pique, 10 de trèfle, 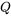 de pique}. La
de pique}. La 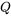 de pique a été pigée deux fois. Chaque sélection est faite parmi le jeu complet (
de pique a été pigée deux fois. Chaque sélection est faite parmi le jeu complet (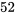 cartes).
cartes). - Échantillonnage sans remplacement :Supposons qu’on sélectionne trois cartes sans remplacement. La première carte choisie sur les
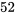 cartes est le
cartes est le 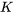 de cœur. On met cette carte de côté, puis on choisit une deuxième carte parmi les
de cœur. On met cette carte de côté, puis on choisit une deuxième carte parmi les 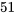 cartes restantes du jeu. Il s’agit du 3 de carreau. On met cette carte de côté, puis on choisit une troisième carte parmi dans les
cartes restantes du jeu. Il s’agit du 3 de carreau. On met cette carte de côté, puis on choisit une troisième carte parmi dans les 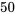 cartes restantes du jeu. La troisième carte est un
cartes restantes du jeu. La troisième carte est un 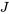 de pique. Les sélections sont {
de pique. Les sélections sont {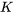 de cœur, 3 de carreau,
de cœur, 3 de carreau, 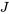 de pique}. Comme les cartes ont été pigées sans remplacement, on ne peut pas piger deux fois la même carte.
de pique}. Comme les cartes ont été pigées sans remplacement, on ne peut pas piger deux fois la même carte.