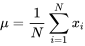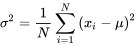2.2.3 Statistiques et paramètres
À ce stade, il est important de présenter un peu plus de terminologie de base. Le jargon et les notations des distributions d’échantillons sont quelque peu différents de ceux des distributions de population (et des distributions théoriques).
DÉFINITION 2.2.3.1. Statistiques et paramètres
Les synthèses numériques des données d’échantillons sont nommées statistiques d’échantillon. Les synthèses numériques de distribution de population ou théoriques sont nommées paramètres (de population ou de modèle). Généralement, on utilise les lettres latines pour les statistiques, et les lettres grecques pour les paramètres.
Prenons l’exemple de la moyenne. La définition 2.2.1.1 porte spécifiquement sur le calcul pour un échantillon. Si un ensemble de données représente une population entière, il est courant d’utiliser la lettre grecque minuscule mu 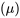 pour représenter la moyenne de la population et de noter :
pour représenter la moyenne de la population et de noter :
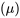 pour représenter la moyenne de la population et de noter :
pour représenter la moyenne de la population et de noter :Moyenne de la population 2.2.3.2.
Si on compare cette expression à celle de la définition 2.2.1.1, on remarque que le symbole utilisé pour la moyenne est différent, et qu’on utilise 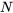 plutôt que
plutôt que  . Il est courant de désigner la taille d’une population par
. Il est courant de désigner la taille d’une population par 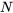 et la taille d’un échantillon par
et la taille d’un échantillon par  .
.
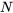 plutôt que
plutôt que  . Il est courant de désigner la taille d’une population par
. Il est courant de désigner la taille d’une population par 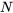 et la taille d’un échantillon par
et la taille d’un échantillon par  .
.Un autre exemple de l’utilisation suggérée par la définition 2.2.3.1 est celui de la variance et de l’écart-type. La définition 2.2.1.2 porte spécifiquement sur la variance et sur l’écart-type de l’échantillon. Si un ensemble de données représente une population entière, il est courant d’utiliser la lettre grecque sigma minuscule au carré (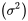 ) pour représenter la variance de la population et pour définir:
) pour représenter la variance de la population et pour définir:
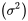 ) pour représenter la variance de la population et pour définir:
) pour représenter la variance de la population et pour définir:Variance de la population 2.2.3.3.
La racine carré positive de 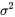 correspond donc à l’écart-type de la population,
correspond donc à l’écart-type de la population, 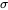 .
.
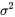 correspond donc à l’écart-type de la population,
correspond donc à l’écart-type de la population, 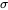 .
.Ce manuel s’écarte de la convention de symbolisme romain/grec exposée dans la définition 2.2.3.1 sur un point : la notation des quantiles. Nous utilisons 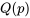 pour représenter le quantile
pour représenter le quantile  d’une distribution, qu’elle soit extraite d’un échantillon, d’une population ou d’un modèle théorique.
d’une distribution, qu’elle soit extraite d’un échantillon, d’une population ou d’un modèle théorique.
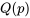 pour représenter le quantile
pour représenter le quantile  d’une distribution, qu’elle soit extraite d’un échantillon, d’une population ou d’un modèle théorique.
d’une distribution, qu’elle soit extraite d’un échantillon, d’une population ou d’un modèle théorique.