2.2.2 Mesures de dispersion
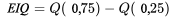 pour représenter la dispersion d’une distribution. L’écart interquartile mesure la répartition de la moitié centrale d’une distribution. Il est donc insensible à quelques valeurs extrêmes éventuelles. Une mesure apparentée est l’étendue, qui indique la dispersion de l’ensemble de la distribution.
pour représenter la dispersion d’une distribution. L’écart interquartile mesure la répartition de la moitié centrale d’une distribution. Il est donc insensible à quelques valeurs extrêmes éventuelles. Une mesure apparentée est l’étendue, qui indique la dispersion de l’ensemble de la distribution.DÉFINITION 2.2.2.1. Étendue
L’étendue d’un ensemble de données constitué de valeurs ordonnées 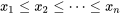 est
est
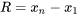
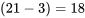 ». Étant donné que l’étendue ne dépend que des valeurs du plus petit point et du plus grand point d’un ensemble de données, elle est nécessairement très sensible aux valeurs extrêmes (ou aberrantes). Parce qu’elle est facile à calculer, elle a longtemps été populaire dans les milieux industriels, notamment en tant qu’outil de contrôle statistique de la qualité.
». Étant donné que l’étendue ne dépend que des valeurs du plus petit point et du plus grand point d’un ensemble de données, elle est nécessairement très sensible aux valeurs extrêmes (ou aberrantes). Parce qu’elle est facile à calculer, elle a longtemps été populaire dans les milieux industriels, notamment en tant qu’outil de contrôle statistique de la qualité.DÉFINITION 2.2.2.2. Variance et écart-type d’un échantillon
La variance de l’échantillon d’un ensemble de données composé des valeurs 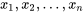 est
est
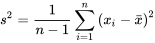
L’écart-type de l’échantillon, 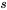 , est la racine carrée positive de la variance de l’échantillon.
, est la racine carrée positive de la variance de l’échantillon.
Sauf pour le remplacement de  par
par  dans le diviseur,
dans le diviseur, 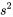 est la distance au carré moyenne des points de données par rapport à la valeur centrale
est la distance au carré moyenne des points de données par rapport à la valeur centrale  . Par conséquent,
. Par conséquent, 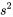 est non négatif, et ne vaut 0 que si tous les points de données sont exactement identiques. Les unités de
est non négatif, et ne vaut 0 que si tous les points de données sont exactement identiques. Les unités de 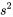 sont le carré des unités des données d’origine. La racine carrée de
sont le carré des unités des données d’origine. La racine carrée de 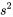 (pour obtenir
(pour obtenir 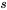 ) produit une mesure de la dispersion exprimée dans les unités d’origine.
) produit une mesure de la dispersion exprimée dans les unités d’origine.
Example 2.2.2.1. Pertes des rouleaux de papier (suite)
La dispersion des deux ensembles de pourcentages de pertes répertoriés dans le tableau 2.2.1.1 peuvent être exprimés dans l’un des termes précédents. Pour le fournisseur 1,
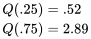
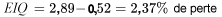
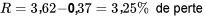
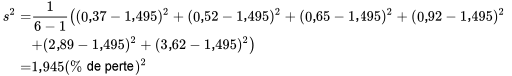
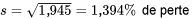
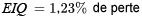
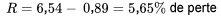
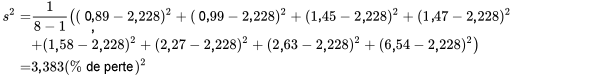
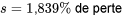
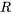 et
et 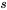 plus grandes. Ceci est cohérent avec la figure 2.2.1.1 : la partie centrale de la distribution du fournisseur 2 est très dense, mais le point extrême rend la variabilité globale plus importante pour le second fournisseur que pour le premier.
plus grandes. Ceci est cohérent avec la figure 2.2.1.1 : la partie centrale de la distribution du fournisseur 2 est très dense, mais le point extrême rend la variabilité globale plus importante pour le second fournisseur que pour le premier.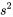 représente une sorte de moyenne du carré de l’écart. Bien entendu, la façon la plus judicieuse de trouver les variances d’échantillon dans la pratique est d’utiliser une calculatrice électronique de poche avec une fonction de variance préprogrammée, ou un logiciel statistique.
représente une sorte de moyenne du carré de l’écart. Bien entendu, la façon la plus judicieuse de trouver les variances d’échantillon dans la pratique est d’utiliser une calculatrice électronique de poche avec une fonction de variance préprogrammée, ou un logiciel statistique.