"

2.1.6 Diagrammes en boîtes

La principale condition préalable pour élaborer des diagrammes en boîtes, un type de graphique qui s’ajoute aux diagrammes de dispersion et aux histogrammes, est de maîtriser la notion de quantiles. Le diagramme en boîtes contient un peu moins d’informations, mais il présente l’avantage qu’on peut en placer plusieurs sur une même page pour les comparer.
Il existe plusieurs conventions courantes pour l’élaboration de diagrammes en boîtes. Celle utilisée ici est illustrée de manière générique à la figure 2.1.6.1. On dessine une boîte qui se rend du premier au troisième quartile, et on ajout une ligne à la médiane. Ensuite, on calcule l’écart interquartile :

DÉFINITION 2.1.6.1. Écart interquartile : EI

E I = Q(0,75) - Q(0,25)

Figure 2.1.6.1. Diagramme en boîtes générique.

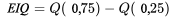
puis, on détermine le plus petit point des données situé dans un intervalle de 1,5 EI de 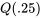Q(0,25) et le plus grand point des données située dans un intervalle de 1,5 EI de 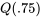Q(0,75). On trace des lignes (les « moustaches ») allant de la boîte à ces valeurs. En général, la plupart des points se situent dans l’intervalle [Q(0,25) - 1,5 E I, Q(0,75) + 1,5 E I]. Ceux qui ne le sont pas sont ajoutés individuellement, ce qui indique qu’il s’agit de valeurs aberrantes ou inhabituelles.

Exemple 2.1.6.2. Quantiles de force de rupture à sec de serviettes en papier (suite)

Créons un diagramme en boîte pour les données sur la force de rupture des serviettes en papier. Pour commencer,

\begin{aligned}Q(0,25) & = 8,572 \mathrm{~g} \\Q(0,5) & = 9,088 \mathrm{~g} \\Q(0,75) & = 9,614 \mathrm{~g}\end{aligned}
Donc
E I = Q(0,75) - Q(0,25) = 9,614 - 8,572 = 1,042 \mathrm{~g}
et
1.5 E I = 1,563 \mathrm{~g}
d’où
Q(0,75) + 1.5 E I = 9,614 + 1,563=11,177 \mathrm{~g}
et
Q(0,25) - 1,5 E I = 8,572 - 1,563 = 7,009 \mathrm{~g}
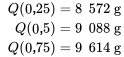
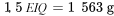
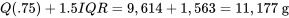
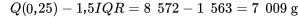
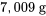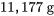Comme tous les points de données se trouvent dans la plage 7,009 \mathrm{~g} to 11,177 \mathrm{~g}, le diagramme en boîtes ressemble donc à la figure 2.1.6.2.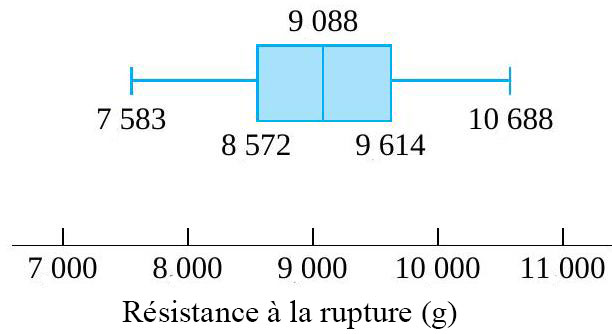

Figure 2.1.6.2. Diagramme en boîtes de la force de rupture de serviettes en papier.
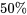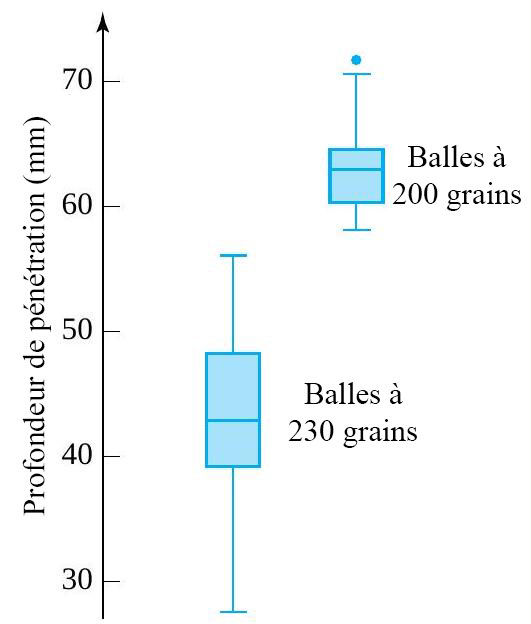
Un diagramme en boîtes illustre la distribution par l’intermédiaire de la boîte, qui englobe le 50 \% du milieu de la distribution, et les moustaches. Certains éléments de la forme de la distribution sont indiqués par la symétrie (ou l’asymétrie) de la boîte et des moustaches. En outre, un espace entre l’extrémité d’une moustache et un point individuel rappelle qu’il n’y a aucune autre valeur dans cet intervalle.
Pour comparer plusieurs échantillons efficacement, on peut juxtaposer leurs diagrammes de boîtes.

Exemple 2.1.6.3 Profondeur de pénétration des balles (suite)

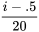Le tableau 2.1.6.1 répertorie les informations brutes nécessaires pour trouver les quantiles \frac{i - 0,5} des deux distributions de profondeur de pénétration des balles présentées à la section précédente. Pour les profondeurs de pénétration des balles de 230 grains, l’interpolation donne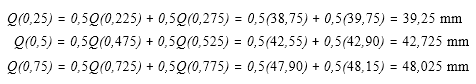
\begin{aligned}Q(0,25) & = 0,5 Q(0,225)+0,5 Q(0,275) = 0,5(38,75) + 0,5(39,75) = 39,25 \mathrm{~mm} \\Q(0,5) & = 0,5 Q(0,475) + 0,5 Q(0,525) = 0,5(42,55) + 0,5(42,90) = 42,725 \mathrm{~mm} \\Q(0,75) & = 0,5 Q(0,725)+0,5 Q(0,775) = 0,5(47,90) + 0,5(48,15) = 48,025 \mathrm{~mm}\end{aligned}
Donc
\begin{aligned}E I & = 48,025 - 39,25 = 8,775 \mathrm{~mm} \\1,5 E I & = 13,163 \mathrm{~mm} \\Q(0,75) + 1,5 E I & = 61,188 \mathrm{~mm} \\Q(0,25) - 1,5 E I & = 26,087 \mathrm{~mm}\end{aligned}
Pour les profondeurs de pénétration des balles de 200 grains, l’interpolation donne
\begin{aligned}Q(0,25) & = 60,25 \mathrm{~mm} \\Q(,5) & = 62,80 \mathrm{~mm} \\Q(0,75) & = 64,35 \mathrm{~mm} \\Q(0,75) + 1,5 E I & = 70,50 \mathrm{~mm} \\Q(0,25) - 1,5 E I & = 54,10 \mathrm{~mm}\end{aligned}

Tableau 2.1.6.1.

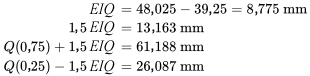
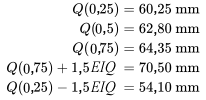
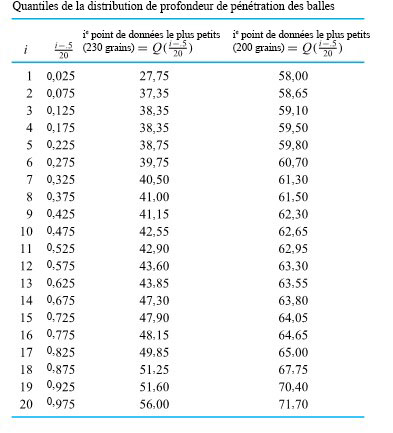
La figure 2.1.6.3 illustre les diagrammes en boîte placées côte à côte sur la même échelle. On constate que les balles de 200 grains ont une profondeur de pénétration plus importante et plus régulière, et on remarque qu’il y a un point particulièrement extrême dans l’ensemble de données de 200 grains. En outre, les longueurs relatives des moustaches indiquent une certaine asymétrie (rappelons la terminologie introduite précédemment pour discuter de la forme de la distribution) dans les données. Et tout ça, dans un graphique très épuré et compact. Il serait possible d’ajouter beaucoup d’autres boîtes à la figure 2.1.6.3 (pour comparer d’autres types de balles) sans alourdir le graphique.

Figure 2.1.6.3. Diagrammes en boîte côte à côte pour la profondeur de pénétration des balles

Licence

Introduction aux méthodes statistiques en ingénierie© par C. Bassim et Bryan Lee. Tous droits réservés.

Partagez ce livre