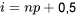2.1.5 Quantiles et diagrammes quantile
La plupart des lecteurs connaissent le concept de percentile (ou rang centile), une notion surtout vue dans le contexte des résultats des examens scolaires. Par exemple, si une personne a obtenu une note la plaçant au 80e rang centile, environ 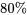 des personnes qui ont passé l’examen ont obtenu une moins bonne note, et
des personnes qui ont passé l’examen ont obtenu une moins bonne note, et 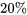 ont obtenu une meilleure note. Ce concept est également utile pour décrire des données d’ingénierie. Toutefois, comme il est souvent plus pratique de travailler en termes de fractions entre 0 et 1 plutôt qu’en termes de pourcentages entre 0 et 100, on utilisera une terminologie légèrement différente : on parlera de « quantiles » plutôt que de rang centiles. Après avoir soigneusement défini les quantiles d’un ensemble de données, on les utilise pour créer divers outils utiles de statistiques descriptives : diagrammes quantile, diagrammes en boîte, diagrammes
ont obtenu une meilleure note. Ce concept est également utile pour décrire des données d’ingénierie. Toutefois, comme il est souvent plus pratique de travailler en termes de fractions entre 0 et 1 plutôt qu’en termes de pourcentages entre 0 et 100, on utilisera une terminologie légèrement différente : on parlera de « quantiles » plutôt que de rang centiles. Après avoir soigneusement défini les quantiles d’un ensemble de données, on les utilise pour créer divers outils utiles de statistiques descriptives : diagrammes quantile, diagrammes en boîte, diagrammes  , et diagrammes normaux (un type de diagramme
, et diagrammes normaux (un type de diagramme  théorique).
théorique).
 compris entre 0 et 1 , le quantile
compris entre 0 et 1 , le quantile  d’une distribution est un nombre tel qu’une fraction
d’une distribution est un nombre tel qu’une fraction  de la distribution se trouve à gauche, et une fraction
de la distribution se trouve à gauche, et une fraction  , à droite. Toutefois, en raison du caractère discret des ensembles finis de données, il est nécessaire d’indiquer exactement ce que l’on veut dire par là. La définition 1 donne la convention qui sera utilisée dans ce texte.
, à droite. Toutefois, en raison du caractère discret des ensembles finis de données, il est nécessaire d’indiquer exactement ce que l’on veut dire par là. La définition 1 donne la convention qui sera utilisée dans ce texte.Définition 3.1.5.1 Quantile 
 valeurs ordonnées
valeurs ordonnées 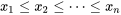 ,
,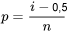 pour un entier positif
pour un entier positif 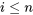 , le quantile
, le quantile  de l’ensemble de données est
de l’ensemble de données est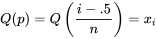
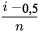 .)
.) compris entre
compris entre 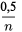 et
et 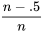 qui n’est pas de la forme
qui n’est pas de la forme 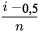 avec
avec  entier, le quantile
entier, le quantile  de l’ensemble de données s’obtient par interpolation linéaire entre les deux valeurs de
de l’ensemble de données s’obtient par interpolation linéaire entre les deux valeurs de 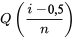 avec les valeurs
avec les valeurs 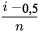 correspondantes qui entourent
correspondantes qui entourent  .
. est dénoté
est dénoté 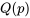 .
.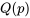 pour tous les
pour tous les  compris entre
compris entre 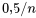 et
et 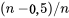 . Pour trouver
. Pour trouver 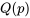 pour une telle valeur de
pour une telle valeur de  , on isole
, on isole  dans
dans 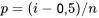 , ce qui donne
, ce qui donneIndex (i) du point de données ordonnées au quantile
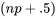 e point de données ordonnées ».
e point de données ordonnées ».Exemple 2.1.5.1. Quantiles de force de rupture à sec de serviettes en papier
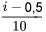 , il est facile de trouver les quantiles d’ordre
, il est facile de trouver les quantiles d’ordre 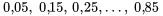 et 0,95 de la répartition de la force de rupture, comme illustré au tableau 2.1.5.2.
et 0,95 de la répartition de la force de rupture, comme illustré au tableau 2.1.5.2.
.
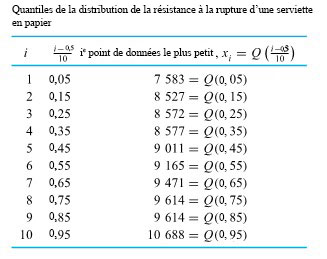
Étant donné qu’il y a 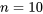 points de données, chacun d’eux compte pour
points de données, chacun d’eux compte pour 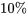 de l’ensemble de données. Appliquons la convention (1) de la définition 3.1.5.1 pour trouver le quantile d’ordre 0,35 (par exemple). Les trois points de données les plus petits et la moitié du quatrième plus petit sont considérés comme se trouvant à gauche du nombre souhaité, et les six points de données les plus grands et la moitié du septième plus grand sont considérés comme se trouvant à droite. Ainsi, le quatrième point de données le plus petit doit être le quantile d’ordre 0,35, comme le montre le tableau 2.1.5.2.
de l’ensemble de données. Appliquons la convention (1) de la définition 3.1.5.1 pour trouver le quantile d’ordre 0,35 (par exemple). Les trois points de données les plus petits et la moitié du quatrième plus petit sont considérés comme se trouvant à gauche du nombre souhaité, et les six points de données les plus grands et la moitié du septième plus grand sont considérés comme se trouvant à droite. Ainsi, le quatrième point de données le plus petit doit être le quantile d’ordre 0,35, comme le montre le tableau 2.1.5.2.
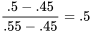 unité à mi-chemin entre 0,45 et 0,55, l’interpolation linéaire donne :
unité à mi-chemin entre 0,45 et 0,55, l’interpolation linéaire donne :
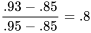 unité à mi-chemin entre 0,85 et 0,93, l’interpolation linéaire donne :
unité à mi-chemin entre 0,85 et 0,93, l’interpolation linéaire donne :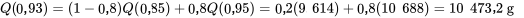
 donne des quantités
donne des quantités 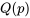 qui portent des noms spéciaux.
qui portent des noms spéciaux.DÉFINITION 2.1.5.2 Médiane
Définition 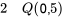 est la médiane de la distribution.
est la médiane de la distribution.
DÉFINITION 2.1.5.3 Premier et troisième quartiles
Définition 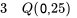 et
et 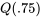 sont respectivement le premier et le troisième quartiles d’une distribution.
sont respectivement le premier et le troisième quartiles d’une distribution.
Exemple 2.1.5.1 Quantiles de force de rupture à sec de serviettes en papier (suite)
Si l’on se réfère à nouveau au tableau 2.1.5.2 et à la valeur de 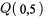 précédemment calculée, pour la distribution de la force de rupture, on a :
précédemment calculée, pour la distribution de la force de rupture, on a :
On peut représenter les quantiles à l’aide d’un diagramme.
DÉFINITION 2.1.5.4 Diagramme quantile
Un diagramme quantile est un graphique de 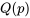 en fonction de
en fonction de  . Pour un ensemble de données ordonnées de taille
. Pour un ensemble de données ordonnées de taille  contenant les valeurs
contenant les valeurs 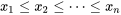 , on obtient ce graphique en traçant les points
, on obtient ce graphique en traçant les points 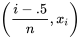 puis en reliant les points consécutifs par des segments de droite.
puis en reliant les points consécutifs par des segments de droite.
C’est la convention (2) de la définition 2.1.5.1, qui demande une interpolation linéaire, qui fait qu’on ajoute des segments de droite au diagramme de quantiles.
Exemple 2.1.5.1. Quantiles de force de rupture à sec de serviettes en papier (suite)
Si l’on se réfère à nouveau au tableau 2.1.5.2 pour les quantiles de la distribution de la force de rupture, il est clair qu’un diagramme quantile pour ces données impliquera de tracer puis de relier les paires ordonnées consécutives suivantes.

Ce graphique se trouve à la figure 2.1.5.1.
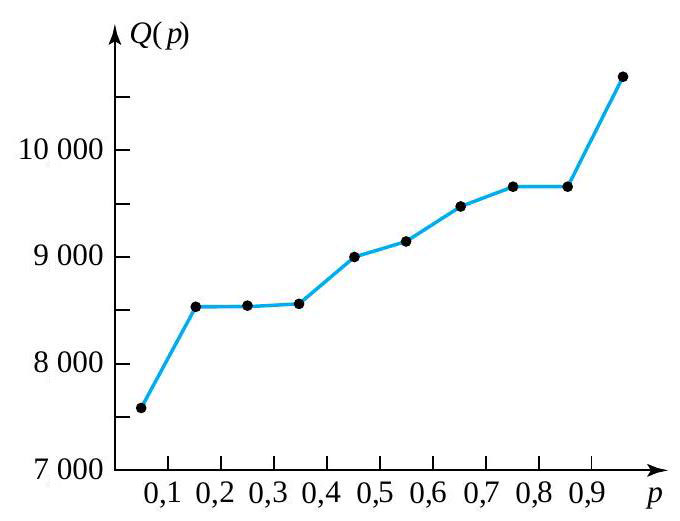
Un diagramme quantile permet d’effectuer de lisser quelque peu les données irrégulières. (On suppose tacitement que pour le mécanisme de génération des données à l’étude, si on augmentait la taille de l’échantillon, on obtiendrait un diagramme quantile plus lisse.)