1.1.7 Modèles mathématiques, réalité et analyse des données
Il est possible d’apprendre les bases de la statistique et les méthodes statistiques de l’ingénierie sans comprendre les mathématiques sous-jacentes. Les statistiques contiennent une bonne quantité de mathématiques que la plupart des ingénieur.e.s trouveront raisonnablement compréhensibles, bien que peu familières et initialement déroutantes. Mais si on adopte une approche mathématique au contexte d’apprentissage, on pave la voir vers une utilisation approfondie et améliorée des méthodes statistiques en ingénierie. C’est aussi une bonne manière d’appliquer la théorie mathématique apprise dans une application pratique. Il semble donc judicieux d’essayer de mettre en perspective le contenu mathématique du livre dès le début. Cette section porte sur les relations entre les mathématiques, le monde physique et les statistiques d’ingénierie.Modèles mathématiques et réalité
Les mathématiques sont une construction et un outil. Bien qu’elles présentent un intérêt en soi pour certaines personnes, les ingénieur.e.s les abordent généralement du point de vue de leur utilité pour décrire et prédire le comportement des systèmes physiques. En effet, les théories mathématiques sont des guides dans toutes les disciplines de génie moderne.
Tout au long de ce texte, nous utiliserons fréquemment l’expression « modèle mathématique ».
DÉFINITION 1.1.7.1. Modèle mathématique
Un modèle mathématique est une description ou un résumé des principales caractéristiques d’un système ou d’un phénomène réel, sous forme de symboles, d’équations, de nombres, etc.
Les modèles mathématiques ne sont pas la réalité, mais ils peuvent être des descriptions extrêmement efficaces de la réalité. Cette efficacité repose sur deux propriétés quelque peu opposées d’un modèle mathématique: 1) son degré de simplicité, et 2) sa capacité de prédiction. Les modèles mathématiques les plus puissants sont ceux qui sont à la fois simples et qui produisent de bonnes prédictions. La simplicité d’un modèle permet d’opérer dans son cadre en utilisant des hypothèses de base pour tirer des conséquences mathématiques, lesquelles forment des prédictions sur le comportement du processus. Lorsque ces prédictions sont empiriquement correctes, c’est que le modèle est un outil efficace.
Les lois de Newton sont un exemple remarquable de modélisation mathématique efficace. Par exemple, la simple affirmation mathématique que l’accélération gravitationnelle est constante,
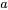 =
= 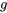
permet, après une opération mathématique facile (une intégration), de prédire qu’après un temps , un objet initialement au repos en chute libre se déplacera à la vitesse
, un objet initialement au repos en chute libre se déplacera à la vitesse
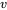 =
= 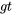
Une deuxième intégration permet de prédire qu’après un temps  , le même objet aura parcouru la distance
, le même objet aura parcouru la distance
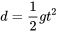
L’avantage est que, dans la plupart des cas, ces prédictions simples sont très adéquates. Elles correspondent bien à ce qui est observé de manière empirique et peuvent être prises en compte lorsqu’on conçoit, construit, exploite ou améliore des processus physiques ou des produits.Modèles mathématiques appliqués aux statistiques
Mais alors, quel rôle la notion de modélisation mathématique joue-t-elle dans les statistiques d’ingénierie? Elle joue plusieurs rôles, en fait. D’une part, la collecte et l’analyse des données sont essentielles pour ajuster ou estimer les paramètres des modèles mathématiques. Pour illustrer cela, reprenons l’exemple du corps en chute libre. Si l’on postule que l’accélération due à la gravité est constante, il reste ensuite à
définir la valeur numérique de cette constante. Il faut évaluer le paramètre 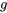 avant d’utiliser le modèle à des fins pratiques. Pour cela, il faut collecter des données.
avant d’utiliser le modèle à des fins pratiques. Pour cela, il faut collecter des données.
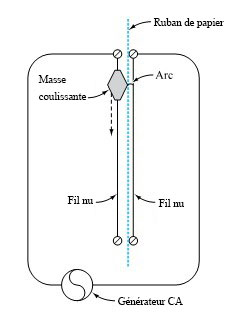
Souvent, au niveau postsecondaire, le premier laboratoire de physique consiste à évaluer empiriquement la valeur de 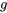 . La méthode la plus couramment utilisée consiste à laisser tomber une masse le long d’un fil vertical passant par un trou en son centre et à laisser un courant électrique de 60 Hz former un arc entre le fil et un autre fil, brûlant légèrement une bande de papier intercalée entre les deux fils à chaque cycle. La figure 1.1.7.1 illustre ce genre de montage. Les marques de brûlure sont indiquent la position de la masse à des intervalles de
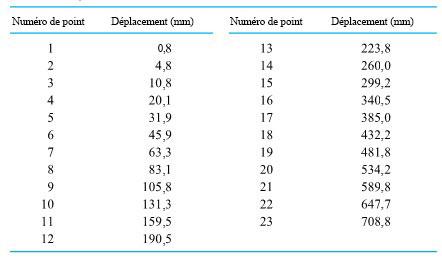
. La méthode la plus couramment utilisée consiste à laisser tomber une masse le long d’un fil vertical passant par un trou en son centre et à laisser un courant électrique de 60 Hz former un arc entre le fil et un autre fil, brûlant légèrement une bande de papier intercalée entre les deux fils à chaque cycle. La figure 1.1.7.1 illustre ce genre de montage. Les marques de brûlure sont indiquent la position de la masse à des intervalles de 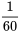 d’une seconde. Le tableau 1.1.7.1 répertorie les mesures de ces positions. (Le ruban a été fourni par Frank Peterson, du département de physique et d’astronomie de l’ISU.) Le tracé des positions de la masse dans le tableau à intervalles égaux produit le tracé approximativement quadratique illustré à la figure 1.1.7.2. Pour obtenir la valeur de
d’une seconde. Le tableau 1.1.7.1 répertorie les mesures de ces positions. (Le ruban a été fourni par Frank Peterson, du département de physique et d’astronomie de l’ISU.) Le tracé des positions de la masse dans le tableau à intervalles égaux produit le tracé approximativement quadratique illustré à la figure 1.1.7.2. Pour obtenir la valeur de 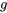 , il suffit de calculer la courbe de régression. La méthode d’ajustement de courbe par moindres carrés donne une valeur de 9,79
, il suffit de calculer la courbe de régression. La méthode d’ajustement de courbe par moindres carrés donne une valeur de 9,79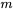 /
/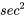 pour g, très proche de la valeur communément admise de 9,8
pour g, très proche de la valeur communément admise de 9,8 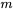 /
/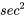 .
.
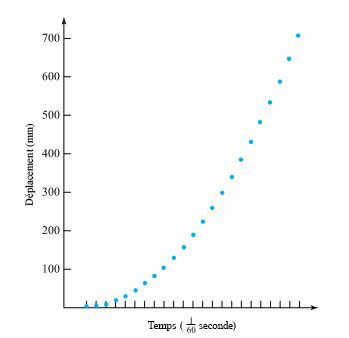
Notez que (au moins, avant Newton) les données du tableau 1.1.7.1 auraient pu être utilisées d’une autre manière. La forme parabolique du tracé de la figure 1.1.7.2 aurait pu suggérer la forme du modèle décrivant le mouvement d’un corps en chute libre. En observant attentivement le tracé de la position en fonction du temps, on devrait conclure qu’il existe une relation approximativement quadratique entre la position et le temps (et, à partir de là, faire deux dérivées pour conclure que l’accélération gravitationnelle est à peu près constante). Ce manuel regorge d’exemples montrant à quel point il peut être utile d’utiliser des données pour, d’une part, identifier des formes potentielles de modèles empiriques et, d’autre part, pour évaluer les paramètres de ces modèles (ce qui nous permettra de les utiliser pour faire des prédictions).
Cette discussion s’est concentrée sur le fait que les statistiques fournissent la matière première pour développer des modèles mathématiques réalistes de systèmes réels. Mais il existe un autre interaction essentielle entre les statistiques et les mathématiques. La théorie mathématique des probabilités fournit un cadre permettant de quantifier l’incertitude associée aux inférences liées aux données.
DÉFINITION 1.1.7.2. Probabilité
La probabilité est la théorie mathématique servant à décrire les situations et les phénomènes que l’on qualifierait familièrement d’aléatoires.
Si, par exemple, cinq étudiant.e.s obtiennent les cinq valeurs expérimentales de 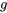 suivantes :
suivantes :
9,78, 9,82, 9,81, 9,78, 9,79
on se demande naturellement comment utiliser ces données pour énoncer à la fois une meilleure valeur pour 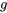 et une certaine mesure de précision pour cette valeur. La théorie des probabilités sert à résoudre ces questions. Le contenu du chapitre 3 montre que les considérations de probabilité permettent d’utiliser la moyenne de la classe de 9,796 pour estimer la valeur
et une certaine mesure de précision pour cette valeur. La théorie des probabilités sert à résoudre ces questions. Le contenu du chapitre 3 montre que les considérations de probabilité permettent d’utiliser la moyenne de la classe de 9,796 pour estimer la valeur 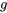 et d’y attacher une précision de l’ordre de ± 0,02
et d’y attacher une précision de l’ordre de ± 0,02 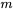 /
/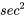 .
.
Les mathématiques des probabilités constituent un sujet à part entière, aussi ce texte ne fournira-t-il qu’une introduction minimale au sujet. Mais il ne faut pas perdre de vue que les probabilités et statistiques ne sont pas synonymes. La probabilité est plutôt une branche des mathématiques et une matière utile en soi. Elle se retrouve dans un cours de statistique en tant qu’outil parce que la variation que l’on observe dans les données réelles est étroitement liée, d’un point de vue conceptuel, à la notion de hasard modélisée par la théorie des probabilités.
