1.1.6 Mesure : Importance et difficultés
La réussite des études d’ingénierie statistique dépend de la capacité à effectuer des mesures. Pour des propriétés physiques, comme la longueur, la masse, la température, etc., les méthodes de mesure sont très courantes et évidentes. Souvent, ces propriétés suffisent à caractériser adéquatement le comportement d’un système d’ingénierie. Mais lorsque c’est impossible, il faut définir précisément ce qui est à observer dans le système, puis faire preuve d’ingéniosité pour créer une méthode de mesure adaptée.
Exemple 1.1.6.1. Mesure de la fragilité
Dans le cadre d’un projet de fin d’études en génie métallurgique, il fallait aider un fabricant à améliorer les performances d’une pièce métallique en forme de pointe. Dans l’application à laquelle elle était destinée, cette pièce devait être solide mais très fragile : lorsqu’elle rencontrait un obstacle sur son chemin, elle devait se briser plutôt que de se plier, car la flexion
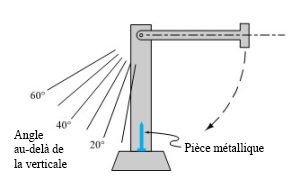
aurait causé d’autres dommages à la machine dans laquelle la pièce fonctionnait. Pendant qu’ils planifiaient une étude statistique visant à déterminer les variables de fabrication qui affectent la performance des pièces, les étudiant.e.s ont réalisé que l’entreprise ne disposait pas d’un bon moyen pour évaluer la performance des pièces. Pour mener à bien leur étude, ils ont mis au point un appareil de mesure qui ressemblait grossièrement à l’illustration de la figure 1.1.7.1. Un bras oscillant avec une grande masse à son extrémité était placé en position horizontale, puis on le libérait pour qu’il aille frapper une pièce d’essai solidement
fixée en position verticale au bas de sa trajectoire. L’angle maximal au-delà de la verticale formé par le bras après l’impact avec la pièce constituait une mesure efficace de la fragilité.
Exemple 1.1.6.2. Mesure de la solidité d’un joint en bois
Dimond et Dix voulaient mener une étude visant à comparer la solidité d’un joint pour une combinaison de trois essences différentes et de trois colles. Comme ils ne disposaient pas d’un appareil d’essai de solidité, ils en ont inventé un. Pour tester un joint, ils ont suspendu un grand récipient à l’une des pièces de bois et y ont versé de l’eau jusqu’à ce le joint se brise sous le poids de l’eau. Connaissant le volume d’eau versé dans le récipient et la densité de l’eau, ils ont pu déterminer la force nécessaire pour briser le joint.
Qu’on utilise une technologie disponible sur le marché ou qu’il faille fabriquer un nouveau dispositif, un certain nombre de questions concernant les mesures doivent être prises en compte, dont la validité, les variations et les erreurs de mesure, l’exactitude et la précision.
DÉFINITION 1.1.6.1. Validité
Une mesure ou une méthode de mesure est considérée comme valide si elle représente de manière utile et correcte une caractéristique importante d’un objet ou d’un système.
On ne saurait trop insister sur l’importance de se poser la question de la validité des mesures avant de se lancer dans une étude d’ingénierie statistique. La collecte des données d’ingénierie coûte de l’argent, et trop souvent, on consacre des ressources considérables à recueillir des données qui, finalement, n’aident pas vraiment à résoudre le problème en question.
Erreur de mesure
La section 1.1.1.1 a souligné qu’en utilisant des données, on est rapidement confronté au fait que la variation est omniprésente. Une partie de ces variations est due au fait que les objets étudiés ne sont jamais exactement les mêmes. Mais une autre partie des variations découle du fait que les processus de mesure ont également leur propre variabilité inhérente. Si on a une échelle de mesure suffisamment précise, il sera impossible – quels que soient les efforts déployés – d’obtenir plusieurs fois la même mesure pour un même objet. Il est naïf d’attribuer toute variation dans les mesures répétées à une mauvaise technique ou à un manque de rigueur. (Bien entendu, une mauvaise technique et un manque de rigueur peuvent accroître la variation des mesures au-delà de ce qui est inévitable).
Un exercice suggéré par W. J. Youden dans son ouvrage Experimentation and Measurements illustre bien la réalité des erreurs de mesure. Essayez de mesure l’épaisseur du papier de ce livre en utilisant la technique suivante : Ouvrez le livre à une page située vers le début et à une page située vers la fin. Saisissez fermement la pile entre les deux pages
entre le pouce et l’index et mesurez l’épaisseur de la pile (à 0,1 mm près) à l’aide d’une règle d’écolier. En divisant l’épaisseur de la pile par le nombre de feuilles de la pile et en consignant le résultat à 0,0001 mm près, vous obtiendrez la mesure de l’épaisseur.
Exemple 1.1.6.3. Mesures d’épaisseur du papier d’un livre
Vous trouverez ci-dessous dix mesures de l’épaisseur du papier, tirées de l’ouvrage Statistics for Experimenters de Box, Hunter et Hunter, effectuées au cours d’un semestre par les étudiant.e.s en ingénierie Wendel et Gulliver.
Wendel : 0,0807,0,0826, 0,0854, 0,0817, 0,0824,
0,0799, 0,0812, 0,0807, 0,0816, 0,0804
Gulliver : 0,0972, 0,0964, 0,0978, 0,0971, 0,0960,
0,0947, 0,1200, 0,0991, 0,0980, 0,1033
La figure 1.1.6.2 présente un graphique de ces données et révèle clairement que même des mesures répétées par une même personne sur un même livre varient, et que les schémas de variation pour deux personnes différentes peuvent être tout à fait différents. (Les valeurs de Wendel sont à la fois plus petites et plus cohérentes que celles de Gulliver.)
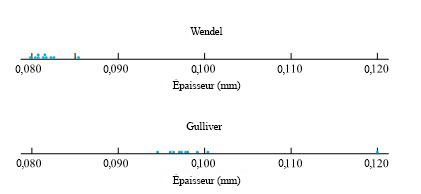
La variabilité qui est inévitable dans les mesures peut être considérée comme ayant des composantes internes et externes.
DÉFINITION 1.1.7.2. Précision
Un système de mesure est dit précis s’il produit de faibles variations lors de mesures répétées du même objet.
La précision correspond à la cohérence interne d’un système de mesure. Généralement, il est possible de l’améliorer en n’opérant que quelques petites modifications dans la configuration du système.
Suite de l’exemple 1.1.6.3.
En ignorant la possibilité qu’une propriété du livre de Gulliver soit à l’origine de la plus grande dispersion de ses valeurs par rapport à celles de Wendel, il apparaît que la technique de mesure de Wendel était plus précise que celle de Gulliver. Il aurait probablement été possible d’améliorer la précision des mesures de Gulliver et de Wendel en leur donnant un trombone et un micromètre. Le trombone exerce une pression relativement constante sur les piles de pages à mesurer, éliminant ainsi la subjectivité et les variations liées à la saisie ferme de la pile entre le pouce et l’index. Pour déterminer l’épaisseur de la pile, le micromètre est un instrument nettement plus précis que la règle.
La précision des mesures est importante, mais pour de nombreux objectifs, elle n’est pas suffisante.
Définition 1.1.7.3 Exactitude
un système de mesure est dit exact (ou parfois, non biaisé) si, en moyenne, il produit la vraie valeur d’une quantité mesurée.
L’exactitude représente la conformité d’un système de mesure à une norme externe quelconque. Il s’agit d’une propriété qui peut généralement être modifiée sans nécessiter de changement physique important à la méthode de mesure. La calibration (aussi appelée étalonnage) d’un système peut être aussi simple que de comparer les mesures du système à un étalon, d’élaborer un schéma de conversion approprié, puis d’utiliser
les valeurs converties au lieu des valeurs brutes du système.
Suite de l’exemple 1.1.6.3.
On ne sait pas ce que la méthode de mesure standard du secteur aurait donné pour l’épaisseur du papier dans la copie du texte de Wendel, mais supposons qu’une valeur de 0,0850 mm/feuille soit appropriée. Le fait que les mesures de Wendel aient été en moyenne de 0,0817 mm/feuille suggère que son exactitude future
pourrait être améliorée en procédant comme précédemment, mais en multipliant tout chiffre obtenu par le rapport 0,0850/0,0817, soit 1,04.
Au Canada, les ensembles de référence des mesures physiques sont établis par Mesures Canada. Aux États-Unis, c’est le National Institute of Standards and Technology qui s’en charge. C’est un travail important. Des appareils de mesure mal calibrés peuvent être suffisants pour comparer les conditions locales, mais pour établir les valeurs des quantités dans un sens absolu, ou pour que les valeurs locales puissent être utilisées en d’autres lieux et à d’autres moments, il est essentiel d’étalonner les systèmes de mesure par rapport à un étalon constant. Un millimètre aujourd’hui en Ontario doit correspondre à un millimètre la semaine dernière en Colombie-Britannique.
Exactitude et études statistiquesLa possibilité de biais ou d’inexactitude dans les systèmes de mesure a au moins deux implications importantes pour la planification des études d’ingénierie statistique. La première, c’est que les appareils doivent être surveillés et recalibrés au besoin. Le phénomène bien connu de la dérive des instruments peut ruiner une étude statistique autrement irréprochable. La deuxième, c’est que dans la mesure du possible, il faut utiliser un seul système pour toutes les mesures. Si on a recours à plusieurs appareils et plusieurs personnes, il devient difficile de déterminer si les différences observées sont attribuables aux variables à l’étude, ou aux instruments et aux gens. S’il faut absolument utiliser plusieurs appareils, ceux-ci doivent être calibrés par rapport à un étalon (ou au moins les uns par rapport aux autres). L’exemple suivant illustre le rôle du facteur humain dans les différences.
Exemple 1.1.6.4. Différences d’utilisation d’une jauge entre plusieurs technicien.ne.s
Cowan, Renk, Vander Leest et Yakes ont travaillé avec une entreprise sur la surveillance d’une dimension critique d’une pièce métallique de haute précision produite sur un tour à commande numérique. Ils ont constaté une variation importante et initialement inexplicable de cette dimension entre les différentes équipes de l’usine. Cette variation a finalement été attribuée
non pas à une différence réelle entre les pièces d’une équipe à l’autre, mais à une instabilité du système de mesure de l’entreprise. Toutes les équipes utilisaient la même jauge pour mesurer la dimension critique, mais pas de la même manière. L’entreprise a donc dû former les technicien.ne.s pour leur montrer à utiliser la jauge d’une seule et unique façon standardisée.
Pour illustrer la différence entre précision et exactitude, prenons l’exemple d’une cible. Si on tire sur la cible, on peut être sur la cible ou en dehors (exactitude), et les tirs peuvent être groupés ou non (précision ou imprécision). La figure 1.1.7.2 illustre cette analogie.
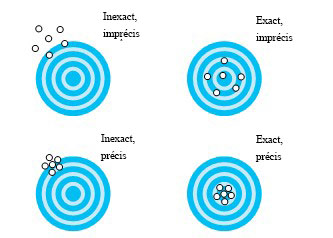
La prise de bonnes mesures est un travail difficile, mais sans elle, la collecte de données est vaine. Pour progresser, il faut obtenir des mesures valides, effectuées par des méthodes suffisamment précises et exactes pour pouvoir identifier les changements importants dans le comportement du système. En règle générale, l’inexactitude et l’imprécision des mesures doivent être inférieures d’un ordre de grandeur à la variation de la réponse causée par ces changements.
