1.1.5 Types de données
Les ingénieur.e.s gèrent de nombreux types de données. Il st souvent utile de les classer selon la mesure dans laquelle elles sont intrinsèquement numériques.
DÉFINITION 1.1.5.1. Données catégoriques
Les données qualitatives ou catégoriques sont les valeurs des caractéristiques fondamentalement non numériques associées aux éléments d’un échantillon. Elles peuvent parfois être ordonnées, mais il faut les agréger et les dénombrer pour produire des valeurs numériques significatives.
Considérons à nouveau un échantillon de cinq pièces de machine tiré d’une caisse de 100 pièces. S’il est possible de classer chaque pièce dans l’une des catégories (ordonnées) 1) conformes, 2) à retravailler, et 3) à jeter, et que l’on connaît les classifications des cinq pièces, on dispose alors de cinq points de données qualitatives. Si l’on dénombre trois pièces conformes, une à retravailler et une à jeter, on se retrouve alors avec un résumé numérique des données catégoriques.
Les données numériques s’opposent aux données catégoriques.
DÉFINITION 1.1.5.2. Données numériques
Les données quantitatives ou numériques sont les valeurs des caractéristiques numériques associées aux éléments d’un échantillon. Il s’agit généralement de compter le nombre d’occurrences d’un phénomène d’intérêt ou de mesurer une propriété physique des éléments.
En reprenant l’exemple des pièces de machine en caisse, les valeurs de dureté de Rockwell des cinq pièces sélectionnées pourraient constituer un ensemble de données (de mesure) quantitatives. Le nombre de défauts visibles sur une surface usinée pour chacune des cinq pièces sélectionnées constituerait un ensemble de données (de dénombrement) quantitatives.
Il est parfois pratique de faire comme si la précision des mesures était infinie. Sous cette hypothèse, les variables mesurées sont continues dans le sens où elles peuvent prendre n’importe laquelle des valeurs appartenant à une plage continue. Par exemple, on peut supposer que la dureté de Rockwell d’une pièce de machine se situe n’importe où dans l’intervalle (0, ∞), mais il ne s’agit bien sûr que d’une idéalisation. En réalité, toutes les mesures sont effectuées à l’unité la plus proche (quelle que soit cette unité). Cela devient d’autant plus évident que les instruments de mesure sont de plus en plus souvent équipés d’écrans numériques. En réalité, lorsqu’on les examine d’assez près, toutes les données numériques (qu’elles soient mesurées ou comptées) sont discrètes, en ce sens qu’elles ne peuvent prendre que certaines valeurs, et non n’importe quelle valeur sur un continuum.
Bien que la plage (0, ∞) soit mathématiquement utile et tout à fait adéquate à des fins pratiques, l’ensemble réel des valeurs possibles pour la dureté de Rockwell mesurée d’une pièce de machine ressemble probablement davantage à {0,1, 0,2, 0,3,…} qu’à (0, ∞).
Il est généralement convenu que les données de mesure sont préférables aux données catégoriques ou de dénombrement. Les méthodes statistiques pour les mesures sont plus simples et plus éclairantes que les méthodes pour les données qualitatives et les dénombrements. En outre, de bonnes mesures nous renseignent généralement beaucoup plus que les données qualitatives. Toutefois, il faut parfois tenir compte du fait que les mesures peuvent prendre plus de temps (et donc coûter plus cher) que la collecte de données qualitatives.
Exemple 1.1.5.1. Mesures de la masse des pastilles
En préliminaire à leur étude expérimentale sur le processus de granulation (abordé dans l’exemple 1.1.3.1), Cyr, Ellson et Rickard ont recueilli des données sur un certain nombre d’aspects du comportement de la machine, dont la masse des pastilles produites dans des conditions d’utilisation normales. Étant donné que la majorité des non conformités résulte d’un détachement du matériau au cours de la production, la masse de la pastille est un indicateur de la performance du système. Les spécifications indiquaient que la masse devait être comprise entre 6,2 et 7,0 g.
Des données sur 200 pastilles ont été recueillies. Les étudiant.e.s auraient pu se contenter d’observer et de noter si une pastille donnée avait une masse conforme aux spécifications, produisant ainsi des données qualitatives, mais ils ont plutôt pris le temps de mesurer la masse des pastilles à 0,1 g près, recueillant ainsi des données de mesure. La figure 1.1.5.1 illustre le résumé de leurs constatations.
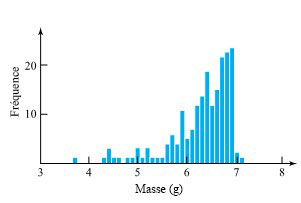
Remarquez qu’il est possible de récupérer les informations de conformité à partir des mesures : environ 28,5% (57 sur 200) des pastilles avaient des masses qui ne répondaient pas aux spécifications. Mais la figure 1.1.5.1 ne se limite pas à cela. La forme de la distribution peut donner des indications sur le fonctionnement de la machine et
sur les conséquences potentielles de simples de modifications du processus de granulation. Par exemple, notez l’aspect tronqué de la figure. La queue avant des données ne ressemble en rien à la queue arrière. Les étudiant.e.s ont déduit que c’était dû au fait qu’après avoir été placée dans une matrice, la poudre passe sous une palette qui élimine l’excès de matière avant qu’un vérin ne la comprime dans la matrice. La quantité initialement distribuée dans une matrice donnée peut avoir une distribution assez symétrique en forme de monticule, mais la palette introduit probablement la caractéristique tronquée de l’affichage.
De plus, à partir des données numériques de la figure 1.1.5.1, on peut trouver un pourcentage de masses de pastilles dans n’importe quel intervalle d’intérêt, et pas seulement dans l’intervalle [6.2, 7.0]. En déplaçant mentalement la figure vers la droite, il est même possible de projeter les effets probables d’une augmentation de la taille des matrices dans des proportions variables.
Dans les études d’ingénierie, il est courant d’avoir plusieurs variables d’intérêt. Les définitions suivantes présentent des termes utiles pour préciser le nombre de variables impliquées et leur relation.
DÉFINITION 1.1.5.3. Données à une seule variable
Les données à une seule variable apparaissent lorsqu’on observe une seule caractéristique de chaque élément de l’échantillon.
DÉFINITION 1.1.5.4. Données à plusieurs variables
Les données à une plusieurs variable apparaissent lorsqu’on observe plusieurs caractéristiques de chaque élément de l’échantillon. Il y a un cas particulier concernant lesdonnées à deux variables.
DÉFINITION 1.1.5.5. Mesures répétées
Lorsque on obtient des données à plusieurs variables en mesurant plusieurs fois une caractéristique essentiellement identique (par exemple, avec des instruments différents ou à des moments différents), on parle de données à mesures répétées. Dans le cas particulier des réponses à deux variables, on parle de données appariées.
Il est important de reconnaître les données à plusieurs variables. Le fait de disposer de valeurs de dureté de Rockwell pour cinq des 100 pièces en caisse de machines et de déterminer le pourcentage de carbone pour cinq autres pièces n’est pas du tout équivalent au fait de disposer à la fois de valeurs de dureté et de teneur en carbone pour un échantillon unique de cinq pièces. Dans le premier cas, il y a deux échantillons de cinq points de données à une seule variable, tandis qu’il n’y a qu’un seul échantillon de cinq points de données à deux variables dans le second. La seconde situation est préférable à la première, car elle
permet d’analyser et de tirer parti de toute éventuelle relation entre les variables « dureté » et « pourcentage de carbone ».
Exemple 1.1.5.2. Mesures de distorsion appariée
Dans le scénario de chargement du four évoqué à l’exemple 1.1.1.1, les mesures de faux-ronds radiaux ont été en fait effectuées sur tous les (38 + 39 =) 77 engrenages avant et après le traitement thermique. (Le tableau 1.1 ne donne que les données après traitement.) On disposait donc de deux échantillons (de tailles respectives 38 et 39) de données appariées. Ainsi, on pouvait (si on le souhaitait) analyser la corrélation entre la distorsion après traitement et la distorsion avant traitement.
