1.1.3 Types d’études et de méthodes statistiques
Lorsqu’on entreprend de collecter des données, il faut décider de son niveau d’activité. Doit-on tourner des boutons et manipuler des variables de procédés, ou doit-on se contenter d’observer et de consigner les caractéristiques qui ressortent?
DÉFINITION 1.2.3.1. Étude d’observation
Une étude d’observation est une étude dans laquelle l’ingénieur.e.s joue un rôle essentiellement passif. On observe un processus ou un phénomène et on consigne les données, mais sans intervenir.
DÉFINITION 1.2.3.2. Étude expérimentale
une étude expérimentale (ou plus simplement, une expérience) est une étude dans laquelle l’ingénieur.e joue un rôle actif. On manipule les variables de processus, et l’environnement de l’étude est contrôlé.
La plupart des études statistiques comprennent des volets d’observation et d’expérimentation; et ces deux définitions doivent être considérées comme les extrémités opposées idéalisées d’un continuum. Sur ce continuum, l’extrémité expérimentale offre généralement les moyens les plus efficaces et les plus fiables de collecter des données d’ingénierie. Il est généralement beaucoup plus rapide de manipuler les variables du processus et d’observer la réaction du système
aux modifications plutôt que d’observer de manière passive, en espérant remarquer un élément intéressant ou révélateur.
Déduction de la causalité
En outre, il est beaucoup plus facile et sûr de déduire la causalité d’une expérience, à partir d’une étude d’observation. Les systèmes réels sont complexes. Il est possible d’observer plusieurs exemples de bons fonctionnements d’un processus et de noter qu’ils ont tous été liés à
des circonstances X sans pour autant supposer que ces circonstances en sont la cause. Il peut y avoir des variables importantes en arrière-plan qui changent et qui sont la véritable raison du bon fonctionnement du système. Ces variables dites « cachées » peuvent régir à la fois le fonctionnement du processus et les circonstances X. Il se peut aussi que de nombreuses variables changent de manière aléatoire, sans avoir d’impact appréciable sur le système et que, par hasard, au cours d’une période d’observation limitée, certaines d’entre elles produisent les circonstances X au même moment où le système fonctionne bien. Dans un cas comme dans l’autre, les efforts pour recréer les circonstances X en espérant que les choses fonctionneront correctement seront des efforts inutiles.
En revanche, dans une expérience où l’environnement est largement régulé, à l’exception de quelques variables qu’on modifie délibérément, la déduction de la causalité est beaucoup plus forte. Si les circonstances de l’étude s’accompagnent systématiquement de résultats favorables, il est raisonnable de penser qu’elles en sont à l’origine.
Exemple 1.1.3.1. Granulation de l’hexamine en poudre
Cyr, Ellson et Rickard ont voulu réduire la portion de pastilles de combustible non conformes produites lors de la compression de poudre d’hexamine brute dans une machine à pastillage. De nombreux facteurs sont susceptibles d’influencer le pourcentage de pastilles non conformes, dont la vitesse de la machine, le remplissage de la filière,
le pourcentage de paraffine ajouté à l’hexamine, la température ambiante, l’humidité lors de la fabrication, la teneur en humidité, la composition « neuve » ou « réutilisée » du mélange à granuler, et la rugosité de la goulotte dans laquelle pénètrent les pastilles fraîchement fabriquées. Il était impossible d’établir une corrélation entre ces nombreux facteurs et les performances du processus par le biais d’une observation passive.
Cependant, les étudiant.e.s ont pu réellement progresser en menant une expérience. Ils ont sélectionné trois des facteurs qui semblaient les plus importants et les ont modifiés tout en maintenant les autres facteurs aussi constants que possible. Les changements importants observés dans le pourcentage de pastilles de combustible acceptables ont été attribués à juste titre à l’influence des variables du système qui avaient été manipulées.
Outre la distinction entre les études statistiques observationnelles et expérimentales, il est utile de distinguer les études en fonction de l’étendue de l’application prévue des résultats. Vous trouverez ci-dessous la définition de deux termes, popularisés par feu W. E. Deming :
DÉFINITION 1.1.3.3. Étude énumérative
Une étude énumérative est une étude dans laquelle il existe un groupe particulier, bien défini et fini d’objets à étudier. Les données sont collectées sur tous ces objets ou sur une partie des objets, et les conclusions visent à s’appliquer uniquement à ces objets.
DÉFINITION 1.1.3.4. Étude analytique
Une étude analytique est une étude dans laquelle un processus ou un phénomène fait l’objet d’une recherche à un point dans l’espace et dans le temps, avec l’espoir que les données collectées seront représentatives du comportement du système à d’autres endroits et à d’autres moments dans les mêmes conditions. Dans ce type d’étude, il existe rarement, voire jamais, de groupe d’objets particulier bien défini auquel les conclusions sont censées se limiter.
En ingénierie, la plupart des études appartiennent à la seconde catégorie, même si certaines applications importantes impliquent un traitement énumératif. L’un de ces exemples est le test de fiabilité des composants critiques – par exemple, pour une utilisation dans une navette spatiale. Ce qui intéresse alors les ingénieur.e.s, ce sont les composants en question et leur performance, et non un problème plus large tel que « le comportement de tous les composants de ce type ». L’échantillonnage d’acceptation (dans lequel on vérifie un lot entrant avant de le réceptionner) représente un autre type significatif d’étude énumérative. Cependant, comme indiqué, la plupart des études liées à l’ingénierie sont de nature analytique.
Suite de l’exemple 1.1.3.1
Les étudiant.e.s qui se penchaient sur la machine de fabrication de pastilles ne s’intéressaient pas à un lot de pastilles particulier, mais plutôt à la question du fonctionnement efficace de la machine. Ils espéraient (ou supposaient tacitement) que ce qu’ils avaient appris sur la fabrication de pastilles resterait valide ultérieurement, au moins dans des conditions identiques à celles où ils ont mené leurs travaux. Leur étude expérimentale était de nature analytique.
Les deux définitions suivantes sont nécessaires, surtout en ce qui a trait aux études énumératives.
DÉFINITION 1.1.3.5. Population
Une population représente un groupe complet d’objets sur lesquels on souhaite collecter des informations dans le cadre d’une étude statistique.
DÉFINITION 1.1.3.6. Échantillon
Un échantillon est un groupe d’objets sur lesquels on souhaite collecter des données. Dans une étude énumérative, l’échantillon est un sous-ensemble de la population (et peut parfois englober la population complète).
La figure 1.1.3.1 illustre la relation entre une population et un échantillon. Si une caisse de 100 pièces de machine est livrée sur un quai de chargement et que 5 pièces sont examinées afin de vérifier l’acceptabilité du lot, les 100 pièces constituent la population d’intérêt et les 5 pièces forment un échantillon (unique) de taille 5 de la population. (Notez l’utilisation des mots ici: il y a un échantillon et non cinq).
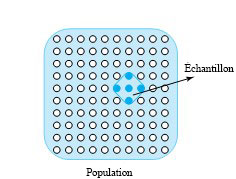
La définition des mots « population » et « échantillon » est souvent élargie de plusieurs façons. D’une part, il est courant de les utiliser pour désigner non seulement les objets étudiés, mais aussi les valeurs des données associées à ces objets. Par exemple, si on l’on considère les valeurs de dureté Rockwell associées à 100 pièces de machine dans une caisse, les 100 valeurs de dureté peuvent être désignées par le terme population (de nombres). Les cinq valeurs de dureté qui correspondent aux pièces examinées (l’échantillon d’acceptation) peuvent être désignées sous le terme d’échantillon tirée de cette population.
Suite de l’exemple 1.1.3.1
Cyr, Ellson et Rickard ont identifié huit ensembles différents de conditions expérimentales pour tester le fonctionnement de la machine à pastilles. Plusieurs cycles de production de pastilles ont été exécutés dans chaque ensemble de conditions, et chacun d’eux a produit son propre pourcentage de pastilles conformes. Ces huit ensembles de pourcentages peuvent désignés comme
huit échantillons (de nombres) différents.
Soit dit en passant, même si aucune population concrète à proprement parler ne fait l’objet d’une recherche dans le cadre d’une étude analytique, il est courant de faire référence à une population conceptuelle dans ce cas. Des expressions telles que « la population composée de tous les objets qui pourraient être produits dans ces conditions » sont parfois utilisées. Cela peut être source de confusion, mais il s’agit d’un usage courant, étayé par le fait que les mêmes mathématiques sont généralement utilisées pour tirer des conclusions dans des contextes énumératifs et analytiques.
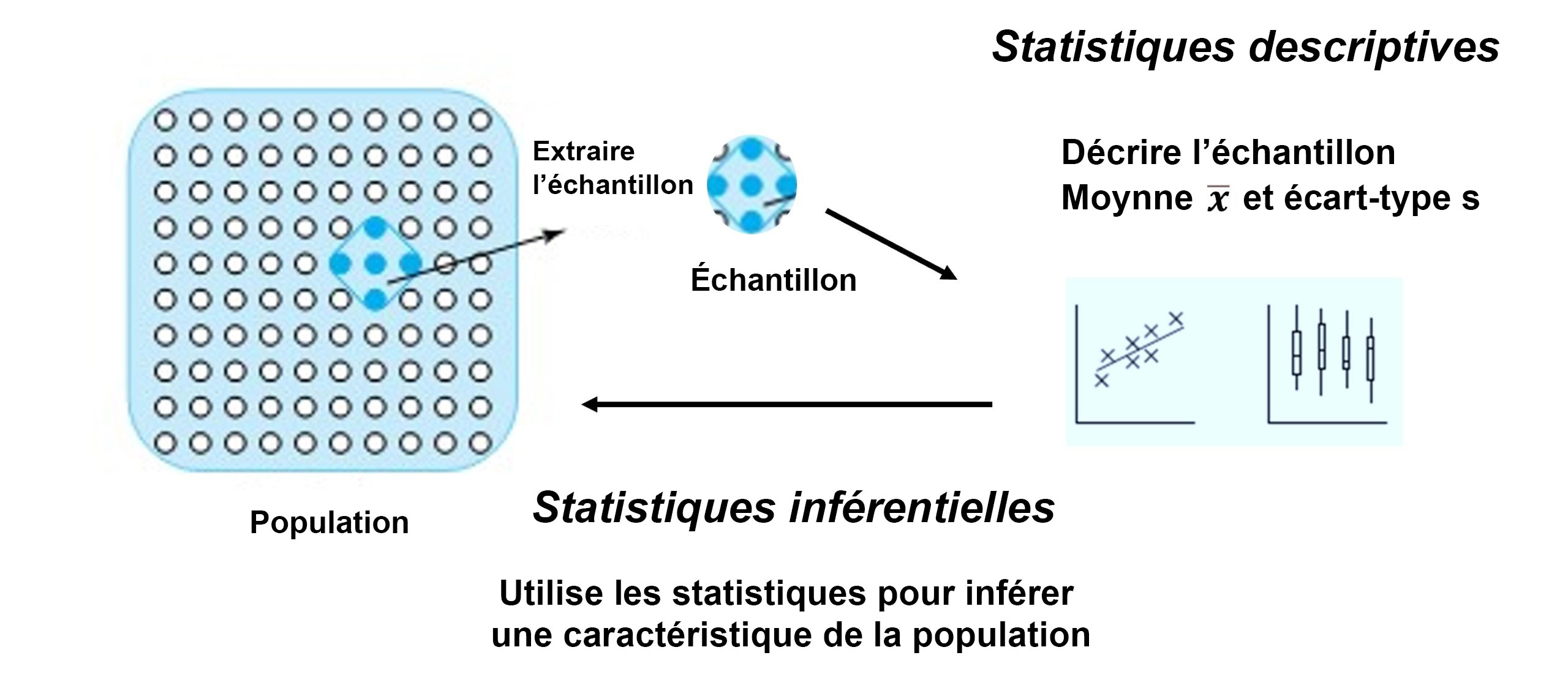
Types de méthodes statistiques
Il y a deux grandes méthodes statistiques pour analyser des données : les statistiques descriptives et les statistiques inférentielles. Les statistiques descriptives résument les données d’un échantillon, par exemple en utilisant sa moyenne et son écart-type. Elles seront le sujet principal de la partie 2 de ce cours. Les statistiques inférentielles permettent de tirer des conclusions à partir de données extraites d’un échantillon soumis à des variations aléatoires. Les statistiques inférentielles s’appuient sur un modèle de probabilité pour décrire le processus à partir duquel les données ont été obtenues, ce que nous verrons dans les parties 3 et 4. Les données sont ensuite utilisées pour tirer des conclusions sur le processus en estimant les paramètres du modèle et en faisant des prédictions basées sur le modèle. Les tests statistiques inférentiels formels seront abordés dans la partie 5 de ce cours. La figure 1.1.2.2 montre comment les statistiques descriptives et inférentielles sont liées.