1.1.1 Méthodes statistiques en ingénierie
En règle générale, le rôle des ingénieur.e.s est de concevoir, de construire, d’utiliser ou d’améliorer des systèmes et des produits physiques. Ce travail repose sur des théories mathématiques et physiques acquises dans un programme de premier cycle en génie. Au fur et à mesure que l’ingénieur.e acquiert de l’expérience, il peut se fier à son jugement en plus des principes quantitatifs et scientifiques. Mais avec l’évolution de la technologie et l’arrivée de nouveaux systèmes et produits, l’ingénieur.e se trouve inévitablement confronté à des questions pour lesquelles la théorie et son expérience ne lui sont pas d’une grande aide. Que faire dans ce cas?
Il est possible de faire appel à des consultants de manière ponctuelle, mais la plupart du temps, il faut se débrouiller tout seul pour comprendre le fonctionnement du système. Pour ce faire, il est nécessaire de collecter et d’interpréter des données. Sans formation sur la collecte et l’analyse des données, les tentatives pourraient être désorganisées ou mal conçues, ce qui entraîne une perte de temps et de ressources, d’autant plus que les conclusions peuvent être erronées (ou inutilement floues). Pour éviter cela, il faut disposer d’une trousse d’outils comprenant les meilleurs principes et méthodes possibles de collecte et d’interprétation des données. Ces outils, ce sont les méthodes statistiques pour l’ingénierie.
L’objectif des statistiques en ingénierie est de fournir les concepts et les méthodes nécessaires lorsqu’on se trouve face à un problème exigeant un jugement indépendant ou une innovation. Elles fournissent les principes d’acquisition et de traitement des données empiriques nécessaires pour comprendre et manipuler les systèmes d’ingénierie.
DÉFINITION 1.1.1.1. Statistiques d’ingénierie
Les statistiques d’ingénierie représentent l’étude de la meilleure façon de
- collecter des données
- résumer ou de décrire les données d’ingénierie
- tirer des inférences formelles et des conclusions pratiques fondées sur des données d’ingénierie, tout en reconnaissant la réalité de la variation.
Pour mieux comprendre cette définition, il est utile de voir comment les statistiques interviennent dans un problème réel.
Exemple 1.1.1.1. Traitement thermique des engrenages.
L’article « Statistical Analysis: Mack Truck Gear Heat Treating Experiments » de P. Brezler (Heat Treating, novembre, 1986) décrit une application simple des statistiques d’ingénierie. Un ingénieur des procédés a dû répondre à la question suivante : « Comment les engrenages doivent-ils être chargés dans un four de cémentation en continu afin de minimiser les déformations pendant le traitement thermique? » Diverses personnes avaient des opinions partiellement informées sur la façon de procéder, notamment sur la question de savoir si les engrenages devaient être empilés ou suspendus à des tiges traversant les alésages, Mais personne ne connaissait vraiment les conséquences de l’empilement ou de la suspension.
Collecte des données
Pour répondre à cette question, l’ingénieur a décidé d’obtenir des faits en recueillant des données sur le faux-rond de la face de poussée (une mesure de la distorsion de l’engrenage) des engrenages empilés et des engrenage suspendus. Le choix des modalités précises de cette collecte de données a nécessité une réflexion approfondie. Il pouvait y avoir des différences entre les lots de matières premières des engrenages, les machinistes et les machines qui produisaient les engrenages, les conditions à différents moments et positions dans le four, les personnes et les appareils de mesure qui produisaient les mesures finales de faux-rond, etc. L’ingénieur ne voulait pas que ces différences soient confondues avec les différences entre les deux techniques de chargement ou qu’elles compliquent inutilement le tableau. Pour l’éviter, il fallait faire preuve de prudence.
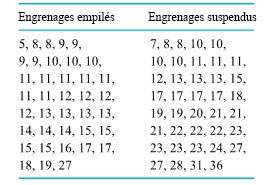
En fait, l’ingénieur a mené de main de maître une étude bien réfléchie. Le tableau 1.1.1.1 répertorie les valeurs de faux-ronds pour 38 engrenages empilés et 39 engrenages suspendus après le traitement thermique. Sous forme brute, ces valeurs n’évoquent pas grand chose. Comme elles ne sont pas organisées, on ne peut pas comprendre le tableau 1.1.1.1 au premier coup d’œil. Les données devaient être résumées.
Résumé des données L’une des actions menées a consisté à calculer des résumés numériques des données. Par exemple, l’ingénieur de procédé a calculé les moyennes de faux-rond suivantes :
engrenages empilés = 12,6
engrenages suspendus = 17,9
Visualisation
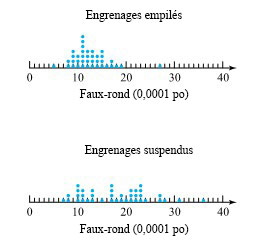
Ensuite, il a résumé les données graphiquement, comme l’illustre la figure 1.1.1.1.
Variation
Grâce à ces résumés, certains faits deviennent évidents. D’abord, les valeurs de faux-ronds varient, même pour une méthode de chargement donnée. La variabilité est un fait omniprésent de la vie, et toute méthodologie statistique le reconnaît explicitement. Dans le cas des engrenages, il ressort de la figure 1.1.1.1 qu’il y a un peu plus de variation dans les engrenages suspendus que dans les engrenages empilés. Mais malgré la variabilité qui complique la comparaison entre les méthodes
de chargement, la figure 1.1.1.1 et les moyennes des deux groupes montrent que le faux-ronds des engrenages empilés est généralement inférieur à celui des faux-ronds des engrenages suspendus. Dans quelle mesure? Calculons la différence :
Faux-rond moyen, engrenages suspendus − faux-rond moyen, engrenages empilés = 5,3
Mais quelle est la précision de ce calcul? Les faux-ronds varient. Peut-on être sûr que la différence observée dans les moyennes
actuelles réapparaîtrait lors d’un autre essai? Ou est-ce simplement du bruit? L’empilement des engrenages coûte plus cher que leur suspension. Peut-on déterminer si ces dépenses supplémentaires sont justifiées?
Représentation des inférences à partir des données
Ces questions soulignent la nécessité d’utiliser des méthodes d’inférence statistique formelle à partir des données et de traduire ces inférences en conclusions pratiques. Les méthodes présentées dans ce texte peuvent, par exemple, être utilisées pour étayer les affirmations suivantes concernant l’empilement et la suspension d’engrenages :
- On peut être sûr à environ 90% qu’à long terme et dans les conditions de l’étude, la différence entre les moyennes est comprise entre
3,2 et 7,4
- On peut être sûr à 95 % que 95 % des faux-ronds des engrenages empilés dans des conditions telles que celles de l’étude de l’ingénieur se situent entre
3,0 et 22,2
- On peut être sûr à 95 % que 95% des faux-ronds des engrenages suspendus dans des conditions telles que celles de l’étude de l’ingénieur se situent entre
0,8 et 35,0
Voilà des quantifications formelles de ce qui a été appris lors de l’étude des engrenages empilés et suspendus. Pour utiliser ces affirmations concrètement, l’ingénieur.e de procédé a dû les combiner avec d’autres informations, comme les conséquences d’un certain niveau de faux-rond et les coûts de suspension et d’empilement des engrenages. Il a aussi dû
faire preuve d’un bon jugement technique. En fin de compte, l’amélioration du faux-rond était suffisamment importante pour justifier une dépense supplémentaire, et la méthode de l’empilement a été instaurée.
Cet exemple démontre comment les statistiques ont contribué à résoudre le problème d’un ingénieur. Tout au long de cet ouvrage, nous allons insister sur le fait que les sujets abordés ne sont pas des fins en soi, mais plutôt des méthodes qu’on peut utiliser pour travailler efficacement.
