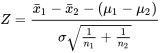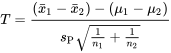5.2.3. Comparaisons de deux moyennes sur un petit échantillon (basée sur des échantillons indépendants suivant une distribution normale)
Les dernières méthodes d’inférence présentées dans cette section correspondent à la différence entre deux moyennes dans les cas où au moins l’une des deux tailles d’échantillon 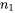 et
et 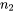 est petite. Toute la discussion se limitera à des cas où les observations sont normales. En fait, les méthodes les plus directes sont réservées aux cas où, en plus, les deux écarts-types sous-jacents sont comparables. Nous commencerons celles-là.
est petite. Toute la discussion se limitera à des cas où les observations sont normales. En fait, les méthodes les plus directes sont réservées aux cas où, en plus, les deux écarts-types sous-jacents sont comparables. Nous commencerons celles-là.
Vérification graphique de la plausibilité du modèle
Un moyen de vérifie sommairement la plausibilité des suppositions du modèle « distributions normales, même variance » consiste à effectuer un tracé normal de deux échantillons sur le même ensemble d’axes, en vérifiant non seulement la linéarité approximative, mais aussi l’égalité approximative de la pente.
Exemple 5.2.3.1 (suite)
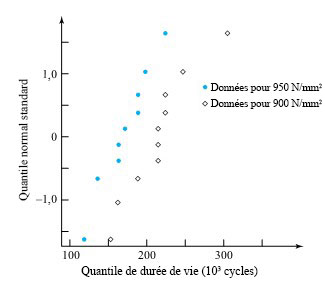
Les données de W. Armstrong sur la durée de vie des ressorts (figurant dans l’ouvrage de Cox et Oakes) concernent non seulement la longévité des ressorts sous une contrainte de 950 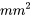 mais aussi sous une contrainte de 900
mais aussi sous une contrainte de 900 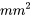 . Le tableau 5.2.3.1 reprend les données de 950
. Le tableau 5.2.3.1 reprend les données de 950 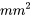 précédentes et y ajoute celles pour la contrainte de 900
précédentes et y ajoute celles pour la contrainte de 900 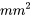 .
.
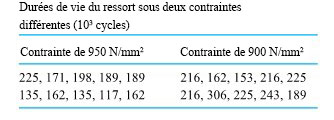
La figure 5.2.3.1 montre des tracés normaux pour les deux échantillons sur un seul ensemble d’axes. Compte tenu du type de variation de la linéarité et de la pente que présentent les tracés normaux pour des échantillons de cette taille (n = 10) issus d’une distribution normale unique, la figure 5.2.3.1 ne constitue nullement une preuve solide contre la pertinence d’un modèle de « variances égales, distributions normales » pour la durée de vie des ressorts.
deux contraintes différentes
Variance pondérée d’un échantillon
Si on suppose que 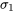 =
= 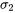 , la valeur commune se nomme σ, et il apparaît logique que
, la valeur commune se nomme σ, et il apparaît logique que 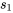 et
et 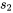 se rapprochent tous deux de σ. Cela suggère qu’il faudrait les combiner pour obtenir une estimation unique de la variation réelle. Il s’avère que la convention mathématique impose une méthode particulière de combinaison ou de pondération des s individuels afin d’obtenir une estimation unique de σ.
se rapprochent tous deux de σ. Cela suggère qu’il faudrait les combiner pour obtenir une estimation unique de la variation réelle. Il s’avère que la convention mathématique impose une méthode particulière de combinaison ou de pondération des s individuels afin d’obtenir une estimation unique de σ.
DÉFINITION Variance pondérée d’un échantillon 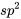
EXPRESSION 5.2.3.1
Si deux échantillons numériques de tailles respectives 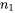 et
et 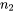 produisent des variances d’échantillon respectives
produisent des variances d’échantillon respectives 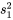 et
et 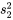 , la variance pondérée de l’échantillon,
, la variance pondérée de l’échantillon, 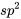 est la moyenne pondérée de
est la moyenne pondérée de 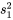 et
et 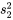 où les coefficients de pondération correspondent aux tailles d’échantillon moins 1. Autrement dit,
où les coefficients de pondération correspondent aux tailles d’échantillon moins 1. Autrement dit,
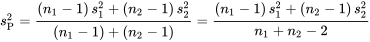
L’écart type pondéré de l’échantillon 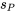 est égal à la racine carrée de
est égal à la racine carrée de 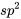 .
.
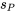 est une sorte de moyenne de
est une sorte de moyenne de 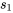 et de
et de 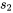 qui se trouve forcément entre
qui se trouve forcément entre 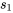 et
et 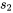 . Sa forme exacte est davantage dictée par souci de convention mathématique que par une intuition logique.
. Sa forme exacte est davantage dictée par souci de convention mathématique que par une intuition logique.
Exemple 5.2.3.2 (suite)
Dans le cas de la durée de vie des ressorts, en choisissant arbitrairement de désigner 900 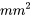 la condition 1 et 950
la condition 1 et 950 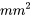 la condition 2, on obtient [latex]s_1 = 42,9 \cdot 10^3[/latex] cycles et
la condition 2, on obtient [latex]s_1 = 42,9 \cdot 10^3[/latex] cycles et 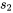 cycles. En regroupant les deux variances de l’échantillon par l’équation 5.2.3.1, on obtient :
cycles. En regroupant les deux variances de l’échantillon par l’équation 5.2.3.1, on obtient :
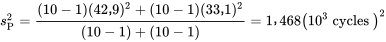
Puis, en prenant la racine carrée, on trouve :
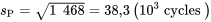
Selon l’argument conduisant aux méthodes d’inférence à grand échantillon pour 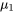 –
– 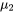 , la quantité
, la quantité
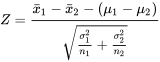
a été brièvement examinée. Lorsque 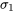 =
= 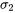 = σ, cette variable peut être réécrite comme suit :
= σ, cette variable peut être réécrite comme suit :
5.2.3.3
On peut exploiter le fait que la variable 5.2.3.3 est normale réduite pour produire des méthodes d’estimation des intervalles de confiance et de tests d’hypothèse. Or, leur utilisation nécessiterait le paramètre σ. Par conséquent, plutôt que de commencer par l’expression 5.2.3.3, il est courant de remplacer σ dans l’expression (5.2.3.3) par 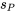 et de commencer par la quantité
et de commencer par la quantité
5.2.3.4
La variable 5.2.3.4 a été construite expressément pour que, selon les suppositions du modèle actuel, elle suive une distribution de probabilité connue et représentée dans un tableau : la distribution t avec 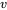 = (
= (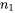 – 1) + (
– 1) + (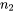 – 1) =
– 1) = 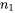 +
+ 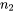 degrés de liberté. (On peut remarquer que les
degrés de liberté. (On peut remarquer que les 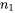 degrés de liberté associés au premier échantillon s’ajoutent aux
degrés de liberté associés au premier échantillon s’ajoutent aux 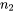 degrés de liberté associés au second pour produire
degrés de liberté associés au second pour produire 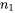
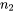 degrés de liberté au total.) Ainsi, toujours au moyen du type de raisonnement développé dans les modules 5.1 et 5.2, on peut obtenir des méthodes d’inférence pour alt\mu_1-alttitle\mu_1-title
degrés de liberté au total.) Ainsi, toujours au moyen du type de raisonnement développé dans les modules 5.1 et 5.2, on peut obtenir des méthodes d’inférence pour alt\mu_1-alttitle\mu_1-title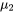 . Autrement dit, un intervalle de confiance bilatéral pour la différence
. Autrement dit, un intervalle de confiance bilatéral pour la différence 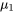
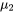 , basé sur des échantillons indépendants provenant de distributions normales de même variance, aura pour bornes
, basé sur des échantillons indépendants provenant de distributions normales de même variance, aura pour bornes
EXPRESSION 5.2.3.5 Bornes confiance pour 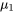
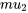 suivant des distributions normales avec
suivant des distributions normales avec 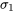 =
= 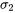
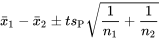
dans laquelle on choisit t de sorte que la probabilité que la distribution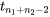 attribue à l’intervalle entre -t et t correspond à la confiance souhaitée. Dans les mêmes conditions, l’hypothèse
attribue à l’intervalle entre -t et t correspond à la confiance souhaitée. Dans les mêmes conditions, l’hypothèse

peut être testée à l’aide de la statistique
EXPRESSION 5.2.3.6 Statistique de test pour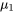
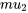 suivant des distributions normales avec
suivant des distributions normales avec 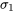 =
= 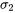
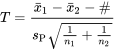
et d’une distribution 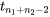 de référence.
de référence.
Exemple 5.2.3.3 (suite)
Reprenons le cas de la durée de vie des ressorts pour illustrer l’inférence pour deux moyennes avec des petits échantillons. Tout d’abord, testons l’hypothèse d’une moyenne de durée de vie égale, avec l’hypothèse alternative que la contrainte plus faible conduit à une durée de vie plus longue. Ensuite, établissons un intervalle de confiance bilatéral à 95 % pour la différence entre les moyennes de durée de vie.
En continuant à désigner la contrainte de 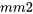 condition 1 et la contrainte de
condition 1 et la contrainte de 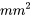 condition 2, à partir du tableau 5.3.3.1, on obtient
condition 2, à partir du tableau 5.3.3.1, on obtient 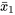 et
et 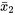 et
et 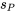 = 38,3 (comme nous l’avons vu précédemment). Ainsi, le modèle de test d’hypothèse en cinq étapes donne ceci :
= 38,3 (comme nous l’avons vu précédemment). Ainsi, le modèle de test d’hypothèse en cinq étapes donne ceci :
1. 
2.  0 . » title= »\mathrm{H}_{\mathrm{a}}: \mu_1-\mu_2>0 . » class= »latex mathjax »>
0 . » title= »\mathrm{H}_{\mathrm{a}}: \mu_1-\mu_2>0 . » class= »latex mathjax »>
(Par raisonnement physique, on s’attend à ce que la condition 1 produise des durées de vie plus longues.)
3.La statistique de test est la suivante :
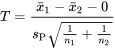
La distribution de référence est t, avec 10 + 10 – 2 = 18 degrés de liberté, et un grand t observé constituera une preuve contre  .
.
4.Les échantillons donnent

5. Le seuil de signification observé [latex]P[\text{une variable aléatoire } t_{ 18} \geq 2,7][/latex] se situe entre 0,01 et 0,005, ce qui constitue une preuve solide que la contrainte faible est associée à une durée de vie plus élevée en moyenne.
Par la suite, si on utilise l’expression 5.2.3.5 pour produire un intervalle de confiance bilatéral à 95 %, t correspond au quantile 0,975 de la distribution 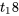 . Les bornes de l’intervalle de confiance pour \
. Les bornes de l’intervalle de confiance pour \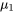 –
– 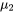 sont les suivantes :
sont les suivantes :

soit :
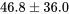
ou encore :
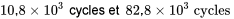
Les données du tableau 5.2.3.1 fournissent suffisamment d’informations pour confirmer qu’une contrainte plus forte entraîne une réduction de la moyenne de durée de vie des ressorts. Mais bien que l’ampleur apparente de cette réduction lors du passage de 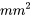 (condition 1) à
(condition 1) à 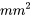 (condition 2) soit de 46,8 10³ cycles, la variabilité présente dans les données est suffisamment grande (et la taille des échantillons suffisamment petite) pour que seule une précision de ±36,0 · 10³ cycles puisse être rattachée à cette différence.
(condition 2) soit de 46,8 10³ cycles, la variabilité présente dans les données est suffisamment grande (et la taille des échantillons suffisamment petite) pour que seule une précision de ±36,0 · 10³ cycles puisse être rattachée à cette différence.
Inférence pour 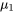 –
– 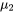 sans la supposition
sans la supposition 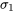 =
= 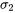 (n = petit)
(n = petit)
Il n’existe pas de réponse pleinement satisfaisante quant à la manière de réaliser l’inférence pour µ1 – µ2 lorsque l’on ne peut pas supposer que 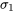
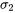 . La méthode la plus répandue (mais approximative) pour résoudre ce problème est celle de Satterthwaite, qui se rapproche de la formule pour les grands échantillons (voir la section 5.2.1). Autrement dit, si les bornes de la section 5.2.1 ne conviennent pas lorsque altn_1alttitlen_1title ou
. La méthode la plus répandue (mais approximative) pour résoudre ce problème est celle de Satterthwaite, qui se rapproche de la formule pour les grands échantillons (voir la section 5.2.1). Autrement dit, si les bornes de la section 5.2.1 ne conviennent pas lorsque altn_1alttitlen_1title ou 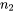 est petit (elles ne produisent pas de niveaux de confiance réels à proximité du niveau nominal), il faut les modifier. Soit
est petit (elles ne produisent pas de niveaux de confiance réels à proximité du niveau nominal), il faut les modifier. Soit
EXPRESSION 5.3.3.7 « Degrés de liberté estimés » de Satterthwaite
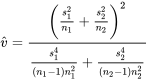
Pour un niveau de confiance souhaité, supposons que 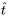 est telle que la distribution
est telle que la distribution 
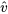 avec
avec 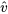 alt\hat{v}alttitle\hat{v}title degrés de liberté attribue la probabilité correspondante à l’intervalle entre
alt\hat{v}alttitle\hat{v}title degrés de liberté attribue la probabilité correspondante à l’intervalle entre 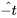 et
et 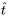 . Ainsi, les deux bornes
. Ainsi, les deux bornes
EXPRESSION 5.2.3.8 Bornes de confiance pour 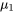
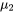 avec la distribution normale (approximative) de Satterthwaite
avec la distribution normale (approximative) de Satterthwaite
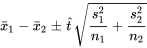
peuvent servir de bornes de confiance pour 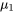 –
– 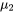 avec un niveau de confiance approximativement égal à celui souhaité. (On peut utiliser une seul des bornes 5.2.3.8 pour obtenir un intervalle de confiance unilatéral en divisant le niveau de « non-confiance » par deux.)
avec un niveau de confiance approximativement égal à celui souhaité. (On peut utiliser une seul des bornes 5.2.3.8 pour obtenir un intervalle de confiance unilatéral en divisant le niveau de « non-confiance » par deux.)
Exemple 5.2.3.4 (suite)
Armstrong a collecté des données sur la durée de vie des ressorts soumis à d’autres contraintes que 900 et 950 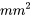 utilisés jusqu’à présent dans cet exemple. Dix ressorts testés à 850
utilisés jusqu’à présent dans cet exemple. Dix ressorts testés à 850 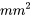 présentaient des durées de vie correspondant à
présentaient des durées de vie correspondant à  (chacune en 10³ cycles) et un tracé normal relativement linéaire. Mais si on examine ensemble les données de 850, 900 et 950
(chacune en 10³ cycles) et un tracé normal relativement linéaire. Mais si on examine ensemble les données de 850, 900 et 950 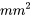 , on voit clairement que les durées de vie deviennent plus courtes et plus uniformes à mesure qu’on augmente la contrainte. Si on compare les moyennes des durées de vie sous les contraintes de 850 et 950
, on voit clairement que les durées de vie deviennent plus courtes et plus uniformes à mesure qu’on augmente la contrainte. Si on compare les moyennes des durées de vie sous les contraintes de 850 et 950 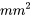 , la supposition d’une variance constante semble douteuse.
, la supposition d’une variance constante semble douteuse.
On peut alors examiner ce que la méthode de Satterthwaite (expression 5.2.3.8) donne comme bornes de confiance bilatérales approximatives à 95 % pour la des moyennes à 850 et à 950 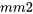 . L’équation 5.2.2.7 donne :
. L’équation 5.2.2.7 donne :

En arrondissant les « degrés de liberté » à l’entier inférieur, le quantile 0,975 de la distribution 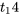 est donc 2,145. Les bornes à 95 % de l’expression 5.3.3.8 pour la différence (
est donc 2,145. Les bornes à 95 % de l’expression 5.3.3.8 pour la différence (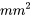
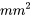 ) des moyennes de durées de vie (
) des moyennes de durées de vie (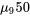 }) sont donc les suivantes :
}) sont donc les suivantes :
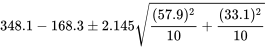
soit :
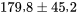
ou encore :
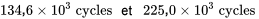
Remarques au sujet des méthodes sur petits échantillons
Les méthodes exposées dans cette section sont les dernières méthodes d’inférence standard pour les moyennes de un ou deux échantillons. Nous étudierons maintenant une méthode parallèle pour les variances. Toutefois, avant de passer à la prochaine section, il convient de faire un dernier commentaire sur les méthodes pour les les petits échantillons.
Nous avons vu qu’à proprement parler, les propriétés nominales (en ce qui concerne les probabilités de couverture pour les intervalles de confiance et les déclarations de valeur p des tests d’hypothèse) des méthodes pour les petits échantillons reposent sur l’hypothèse que les distributions sous-jacentes sont exactement normales et, dans le cas des méthodes 5.2.3.5 et 5.2.3.6, que les variances sont exactement égales. D’autre part, lorsqu’on a utilisé ces méthodes, des vérifications plutôt rudimentaires des tracés de probabilité ont été utilisées à des fins de vérification (seulement) du caractère à peu près plausible des modèles. Selon la théorie statistique conventionnelle, les méthodes pour petits échantillons exposées ici présentent un degré de fiabilité considérable, sauf en cas d’écarts flagrants par rapport aux suppositions du modèle. Autrement dit, tant que les suppositions du modèle représentent à peu près la réalité, les niveaux de confiance nominaux et les valeurs p resteront raisonnablement corrects. (Par exemple, une méthode d’intervalle de confiance nominale de 90 % peut en réalité correspondre à un intervalle de confiance de 80 %, mais pas à un intervalle de confiance de 20 %.) Par conséquent, l’utilisation des graphiques que nous avons faite ici représente généralement une mesure de précaution adéquate contre l’application injustifiée des méthodes d’inférence pour les moyennes de petits échantillons.