5.1.4 Tests d’hypothèse pour moyennes généralement applicables (n = grand)
La méthode de test d’hypothèse utilisée pour mener la discussion jusqu’ici est facile à expliquer et à comprendre, mais son utilisation pratique est limitée en raison de la présence du paramètre σ dans la statistique 5.1.2.4. Comme indiqué au chapitre 5.1.1, il existe peu de contextes d’ingénierie dans lesquels il est nécessaire de faire des déductions concernant µ tout en connaissant la valeur de σ correspondante. Heureusement, en raison du même fait de la théorie des probabilités qui a permis de produire une formule d’intervalle de confiance pour µ sans σ dans le cas d’un grand échantillon, il est également possible de réaliser des tests d’hypothèse pour µ sans avoir à fournir σ dans le cas d’un grand échantillon.
Pour les observations qui peuvent être décrites comme essentiellement équivalentes à des sélections aléatoires avec remplacement dans une population unique avec une moyenne µ et une variance σ², si n est grand,
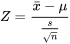
est approximativement normale réduite. Cela signifie que pour un grand n, pour tester
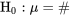
dans la plupart des cas, il suffira d’appliquer la logique déjà présentée mais avec la statistique
EXPRESSION 5.1.4.1 Statistique de test pour 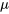 (n = grand)
(n = grand)
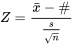
à la place de la statistique 5.1.2.4.
Exemple 5.1.4.1. Test d’hypothèse et défaillance de disque dur (suite)
Prenons le cas d’une défaillance du code de clignotement A d’un disque dur. Les couples de rupture ajustés en usine sur la connexion de l’indicateur d’interrupteur à l’arbre du moteur pas à pas étaient en moyenne de 33,5 po oz, et on soupçonnait que la défaillance du code de clignotement A était associée à un couple de rupture réduit. Rappelons qu’un échantillon de n = 26 disques durs défectueux présentait des couples de rupture (indiqués à la figure 5.1.2.2) de  = 11,5 po oz et s = 5,1 po oz.
= 11,5 po oz et s = 5,1 po oz.
Si on souhaite déterminer dans quelle mesure les données infirment la possibilité que les disques présentant une défaillance du code de clignotement A ont un couple de rupture moyen égal à la valeur moyenne définie en usine de 33,5 po oz. Le modèle de test d’hypothèse en cinq étapes peut être utilisé.
1. : µ = 33,5.
: µ = 33,5.
2.  : µ < 33,5.
: µ < 33,5.
(Ici, l’hypothèse alternative est directionnelle et se résume à une hypothèse de recherche basée sur les soupçons de l’ingénieur.e concernant la relation entre la défaillance du disque et le couple de rupture.)
3.La statistique de test est la suivante :
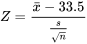
La distribution de référence est normale réduite, et de petites valeurs de z observées constitueront une preuve contre la validité de  . (Les moyennes inférieures à 33,5 tendent à produire des valeurs
. (Les moyennes inférieures à 33,5 tendent à produire des valeurs  petites – c’est-à-dire, des grandes valeurs de z négatives.)
petites – c’est-à-dire, des grandes valeurs de z négatives.)
4. L’échantillon donne
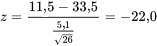
5. Le seuil de signification observé est :
P [une variable normale standard < −22,0] ≈ 0
L’échantillon fournit des preuves irréfutables que les disques défectueux ont un couple de rupture moyen inférieur au niveau défini en usine.
Il est important de ne pas faire un saut logique trop important et de ne pas conclure à tort que c’est là la solution complète au véritable problème d’ingénierie. Les disques durs renvoyés pour une défaillance du code de clignotement A ont un couple de rupture inférieur aux normes, mais en l’absence de preuve du contraire, il est possible qu’ils ne soient pas différents, à cet égard, des disques durs non défaillants actuellement utilisés. Et même si la réduction du couple de rupture est en cause, une solution réelle nécessite l’identification et la prévention du mécanisme physique qui en est à l’origine. Nous ne disons pas que le test d’hypothèse manque d’importance; nous vous rappelons seulement qu’il ne s’agit que de l’un des nombreux outils utilisés pour effectuer le travail d’ingénieur.e.
