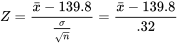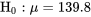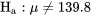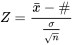Objectif des tests d’hypothèse

Le chapitre précédent a illustré la façon dont les probabilités peuvent permettre d’estimer un intervalle de confiance. Ce chapitre présente en parallèle les tests d’hypothèse.

Les tests d’hypothèse consistent à utiliser des données pour évaluer quantitativement la plausibilité d’une valeur d’essai d’un paramètre (ou d’une fonction d’un ou plusieurs paramètres). Cette valeur d’essai représente généralement le statu quo ou l’estimation pré-expérimentale. Par exemple, en ingénierie des procédés, on peut utiliser des tests d’hypothèse pour évaluer la plausibilité que le procédé actuel utilisé pour remplir des pots de nourriture pour bébés produise effectivement un remplissage moyen correspondant à la valeur idéale de 138 g. Ou encore, deux méthodes différentes de fonctionnement d’une machine de granulation peuvent avoir des propensions inconnues à produire des pastilles défectueuses (disons, p₁ et p₂), et le test d’hypothèse servir à évaluer la plausibilité de p₁ – p₂ = 0 (c’est-à-dire, que les deux méthodes sont aussi efficaces l’une que l’autre).

Cette section explique comment les notions de base des probabilités conduisent à des expressions simples pour les tests d’hypothèse concernant la moyenne µ d’une grand échantillon. Elle présente la terminologie des tests d’hypothèses dans le cas où l’écart-type σ est connu. Ensuite, un format en cinq étapes pour résumer les tests d’hypothèses est présenté. On considère ensuite le cas, plus général, des tests d’hypothèse pour µ lorsque σ n’est pas connu. La section se termine par deux discussions sur des questions pratiques liées à l’application de la logique des tests d’hypothèses.

Tests d’hypothèse pour 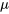impliquant 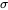(n = grand)

Rappelez-vous l’exemple 4.1.4.3, qui concernait un processus de remplissage physiquement stable, dont l’écart-type de poids net était de σ = 1,6 g. Supposons en outre qu’avec un poids déclaré (sur l’étiquette) de 135 g, les ingénieurs de processus ont fixé un poids net moyen cible de 135 + 3σ = 139,8 g. Enfin, supposons que lors d’un contrôle de routine du processus de remplissage destiné à détecter tout changement de la moyenne du processus par rapport à sa valeur cible, un échantillon de n = 25 pots a produit  = 139.0 g. Qu’est-ce que cette valeur nous apprend sur la plausibilité que la moyenne actuelle du processus respecte bien l’objectif de 139,8 g?

Le théorème centra limite peut être invoqué ici. Si effectivement la moyenne actuelle du processus est de 139,8 g, a une distribution approximativement normale avec une moyenne de 139,8 g et un écart-type σ/√n = 1,6/√25 = 0,32 g, comme le montre la figure 5.1.2.1, qui montre aussi la valeur observée de  = 139,0 g.

La figure 5.1.2.2 illustre l’image normale standard qui correspond à la figure 5.1.2.1. Elle repose sur le fait que si la moyenne actuelle du processus est conforme à l’objectif de 139,8 g, alors le fait que soit approximativement normal avec une moyenne µ et un écart-type σ/√n = 0,32 g implique que

5.1.2.1                    

est approximativement normale réduite. La valeur  = 139,0 g observée à la figure 5.1.2.1 correspond
à la valeur de z = −2,5 à la figure 5.1.2.2.

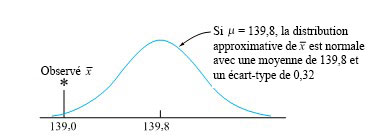
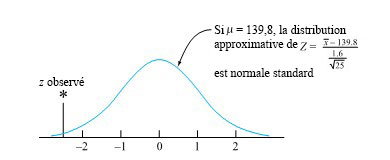
La figure 5.1.2.1 et la figure 5.1.2.2 montrent clairement que si la moyenne du processus est conforme à l’objectif de 139,8 g (et que les chiffres sont donc corrects), on a observé une valeur de (ou une valeur de z associée) assez extrême ou rare. Bien sûr, il arrive que des phénomènes extrêmes ou rares se produisent, mais la valeur de (et de z) observée semble plutôt infirmer l’hypothèse que le processus se déroule comme prévu.

Les chiffres suggèrent même un moyen de quantifier leur propre invraisemblance, soit de calculer la probabilité associée aux valeurs de (ou Z ) au moins aussi extrême que celle observée. L’expression « au moins aussi extrême » doit maintenant être définie par rapport à l’objectif initial de la collecte de données, à savoir détecter une valeur de µ inférieure ou supérieure à la valeur cible. Les valeurs de  ≤ 139,0 g (z ≤ −2,5) sont aussi extrêmes que celle observée, et ce serait également le cas des valeurs de  ≥ 140,6 g (z ≥ 2,5). (Dans le premier cas, suggérerait une valeur de µ inférieure à la cible; dans le second, une valeur supérieure.) En d’autres termes, l’invraisemblance d’être sur la cible peut être quantifiée en notant que si c’était le cas, seule une fraction de

de tous les échantillons produirait la valeur (ou z ) aussi extrême que celle
observée. Cela revient à dire que les données infirment assez fortement l’hypothèse selon laquelle le processus respecte sa cible.

L’argument qui vient d’être présenté est une application de la logique typique du test d’hypothèse. Afin de rendre le fil de pensée évident, il est utile d’en isoler certains éléments sous forme de définition. La définition 5.1.2.1 aborde cette tâche en reformulant l’objectif général des tests d’hypothèse.

Logiquement, les tests d’hypothèses commencent par la spécification de l’essai ou de la valeur hypothétique. Il existe une terminologie et une notation pour énoncer cette valeur.

La notion d’hypothèse nulle est vraiment centrale dans les tests d’hypothèse. La partie « nulle » de l’expression « hypothèse nulle » fait référence au fait que les hypothèses nulles sont des déclarations d’absence de différence, ou autrement dit, d’égalité. Par exemple, dans le contexte du remplissage des pots, l’usage standard serait d’écrire

5.1.2.2                   

ce qui signifie qu’il n’y a pas de différence entre µ et la valeur cible de 139,8 g.

Après avoir formulé une hypothèse nulle, il faut préciser quels types d’écarts par rapport à cette hypothèse sont intéressants.

Souvent, l’hypothèse alternative repose sur les soupçons et ou les espoirs de l’ingénieur.e quant à la situation réelle, ce qui équivaut à une sorte d’hypothèse de recherche qu’on espère démontrer. Par exemple, si on teste ce qui est censé être un dispositif permettant d’améliorer la consommation d’essence d’une automobile, on pourrait émettre l’hypothèse nulle « pas de changement à la consommation d’essence » et l’hypothèse alternative « réduction de la consommation ».

Les définitions 5.1.2.2 et 5.1.2.3 impliquent toutes deux que, dans le cas d’un test portant sur une moyenne unique, les trois paires possibles d’hypothèses nulle et alternative sont les suivantes :

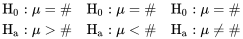\# & \mathrm{H}_{\mathrm{a}}: \mu\# & \mathrm{H}_{\mathrm{a}}: \mu

Dans l’exemple du remplissage des pots, il faut détecter à la fois la possibilité de sous-remplissage (µ < 139,8 g) et la possibilité de surremplissage (µ > 139,8 g). Par conséquent, l’hypothèse alternative suivante est appropriée :

5.1.2.3                   

Une fois que les hypothèses nulle et alternative ont été établies, il faut définir soigneusement la manière dont les données seront utilisées pour évaluer la plausibilité de l’hypothèse nulle. Cela implique de spécifier une statistique à calculer, une distribution de probabilité appropriée si l’hypothèse nulle est vraie, et les types de valeurs observées qui infirmeront l’hypothèse nulle.

Les valeurs de la statistique de test considérées comme mettant en doute la validité de l’hypothèse nulle sont spécifiées après avoir examiné la forme de l’hypothèse alternative. En gros, on identifie les valeurs qui ont plus de chances de se produire si la réalité correspond à l’hypothèse alternative plutôt qu’à l’hypothèse nulle.

La discussion sur le processus de remplissage a oscillé entre l’utilisation de et sa version normalisée z donnée par l’équation 5.1.2.1 pour les statistiques de test. L’équation 5.1.2.1 est une forme spécialisée de la statistique de test générale pour µ (avec n grand et σ connu) :

5.1.2.4                    

pour le cas actuel, où, selon l’hypothèse, µ = 139,8 g, avec n = 25 et σ = 1,6. Il est plus pratique d’envisager la statistique de test pour ce type de problème sous la forme normalisée présentée dans l’équation 5.1.2.4 plutôt que sous la forme 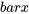. En utilisant la forme 5.1.2.4, la distribution de référence sera toujours la même, à savoir la distribution normale réduite.

En poursuivant avec l’exemple du remplissage, notons que si au lieu de l’hypothèse nulle 5.1.2.2, c’est l’hypothèse alternative 5.1.2.3 qui prévaut, on aura tendance à observer des valeurs de soit beaucoup plus grandes, soit beaucoup plus petites que 139,8 g. L’équation 5.1.2.4 permettra alors de transformer les valeurs de en des valeurs observées de Z grandes ou petites (c’est-à-dire de grands nombres négatifs dans ce cas) – c’est-à-dire de grandes valeurs de |z|. De telles valeurs observées rendent l’hypothèse nulle peu plausible.

Après avoir indiqué comment les données seront utilisées pour juger de la plausibilité de l’hypothèse nulle, il reste à les collecter, à les introduire dans l’expression de la statistique de test et, en utilisant la valeur calculée et la distribution de référence, à parvenir à une évaluation quantitative de la plausibilité de . Il existe un terme pour cela.

Les petites valeurs p infirment .

Plus le seuil de signification observé est faible, plus la preuve de la validité de l’hypothèse nulle est forte. Dans le cadre de l’opération de remplissage, la valeur observée de la statistique de test étant z = −2,5,

le seuil de signification observé associé vaut

ce qui constitue une preuve assez forte contre la possibilité que la moyenne du processus soit conforme à l’objectif.