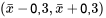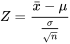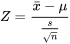5.1.1 Intervalles de confiance de la moyenne d’un grand échantillon
Intervalles de confiance de la moyenne d’un grand échantillon
De nombreuses applications importantes des statistiques dans le domaine de l’ingénierie s’inscrivent dans le moule standard suivant. Les valeurs des paramètres d’un processus de génération de données sont inconnues, et l’objectif est d’utiliser des données pour
- trouver un intervalle de valeurs susceptible de contenir un paramètre inconnu (ou une fonction d’un ou plusieurs paramètres) et
- quantifier la « probabilité » que l’intervalle couvre la valeur correcte.
.
Par exemple, un équipement qui distribue des aliments pour bébés dans des pots peut produire un niveau de remplissage moyen µ inconnu. Il peut être important de déterminer un intervalle basé sur des données susceptible de contenir µ et d’évaluer la fiabilité de l’intervalle. Ou encore, une machine qui usine des filetages sur des boulons en U peut présenter une variation inhérente dans la longueur des filetages, que l’on peut décrire en termes d’écart-type σ. Le but de la collecte de données pourrait alors être de produire un intervalle de valeurs probables pour σ en précisant le degré de confiance de l’intervalle. Ou encore, deux méthodes différentes de fonctionnement d’une machine de granulation peuvent avoir des propensions inconnues différentes à produire des granulés défectueux (disons, p1 et p2). Il pourrait falloir utiliser les données pour trouver un intervalle pour p1 – p2 et fournir le niveau de confiance associé à cet intervalle.
.
DÉFINITION 5.1.1.1 Intervalle de confiance
Un intervalle de confiance pour un paramètre (ou une fonction d’un ou de plusieurs paramètres) est un intervalle numérique basé sur des données et considéré comme susceptible de contenir le paramètre (ou la fonction d’un ou de plusieurs paramètres), avec un certain niveau de confiance (ou de fiabilité) établi selon la théorie des probabilités.
Cette section traite de la façon dont les fondements de la probabilité conduisent à des formules simples pour trouver les intervalles de confiance de la moyenne µ d’un grand échantillon. Le cas inhabituel où l’écart-type σ est connu est traité en premier. Un raisonnement parallèle permet ensuite d’obtenir une formule pour la situation beaucoup plus courante où σ n’est pas connu. La section se termine par des discussions sur trois questions pratiques liées à l’application des intervalles de confiance.
Intervalle de confiance pour 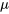 impliquant
impliquant 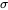 (n = grand)
(n = grand)
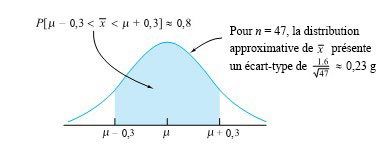
L’exemple 4.1.4.3 concernait un processus de remplissage physiquement stable, dont l’écart-type de poids net était de σ = 1,6 g. Étant donné que, pour un grand n, la moyenne d’échantillon des variables aléatoires iid est approximativement normale, cet exemple a montré que pour n = 47 et
 = le poids net de remplissage moyen de l’échantillon de 47 pots remplis par le procédé (g)
= le poids net de remplissage moyen de l’échantillon de 47 pots remplis par le procédé (g)
il y a environ 80 % de chances que  soit à 0,3 gramme de µ. Ce fait est illustré à nouveau à la figure 5.1.1.1.
soit à 0,3 gramme de µ. Ce fait est illustré à nouveau à la figure 5.1.1.1.
Conventions de notationÀ ce stade, nous devons nous consacrer à la notation. Dans la partie 4, les lettres majuscules ont été soigneusement utilisées pour dénoter les variables aléatoires, et les lettres minuscules correspondantes, pour les valeurs possibles ou observées. Mais ici, nous utilisons un symbole minuscule,  comme variable aléatoire de la moyenne de l’échantillon. Il s’agit là d’un usage statistique assez courant, qui correspond au type de convention utilisé dans les parties précédentes. Nous allons donc abandonner le respect strict de la convention des majuscules introduite à la partie 4. Les variables aléatoires sont souvent symbolisées par des lettres minuscules, et les mêmes symboles sont utilisés pour les valeurs observées. La convention des majuscules de la partie 4 est particulièrement utile pour apprendre les bases de la probabilité. Mais une fois ces bases maîtrisées, il est courant d’abuser de la notation et de déterminer à partir du contexte s’il s’agit d’une variable aléatoire ou de sa valeur observée.
comme variable aléatoire de la moyenne de l’échantillon. Il s’agit là d’un usage statistique assez courant, qui correspond au type de convention utilisé dans les parties précédentes. Nous allons donc abandonner le respect strict de la convention des majuscules introduite à la partie 4. Les variables aléatoires sont souvent symbolisées par des lettres minuscules, et les mêmes symboles sont utilisés pour les valeurs observées. La convention des majuscules de la partie 4 est particulièrement utile pour apprendre les bases de la probabilité. Mais une fois ces bases maîtrisées, il est courant d’abuser de la notation et de déterminer à partir du contexte s’il s’agit d’une variable aléatoire ou de sa valeur observée.
.
La façon la plus courante d’analyser un graphique comme celui de la figure 5.1.1.1 est de le voir comme la probabilité que
5.1.1.1 <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/c637a12264a4b56921ee3431df9c1b86.png » alt= »\mu-0,3<\bar{x}<\mu+0,3″ title= »\mu-0,3<\bar{x}
Autrement dit, il s’agit de la probabilité que  se situe dans un intervalle centré sur µ et de longueur 2(0,3) = 0,6. Mais on peut aussi voir cela comme la probabilité qu’un intervalle centré sur
se situe dans un intervalle centré sur µ et de longueur 2(0,3) = 0,6. Mais on peut aussi voir cela comme la probabilité qu’un intervalle centré sur  et de longueur 0,6 comprenne µ. Algébriquement, l’inégalité 5.1.1.1 est équivalente à
et de longueur 0,6 comprenne µ. Algébriquement, l’inégalité 5.1.1.1 est équivalente à
5.1.1.2 <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/0b4f461aa5a2a1418b4d9a7b53ac7b90.png » alt= »\bar{x}-0,3<\mu<\bar{x}+0,3″ title= »\bar{x}-0,3<\mu
Cependant, cette nouvelle inégalité change l’éclairage du problème. Le fait que l’expression 5.1.1.2 ait environ 80 % de chances d’être vraie chaque fois qu’un échantillon de 47 poids de remplissage est prélevé suggère que l’intervalle aléatoire
5.1.1.3
peut être utilisé comme intervalle de confiance pour µ, avec une fiabilité ou une confiance associée de 80 %.
Exemple 5.1.1.1 Intervalle de confidence pour le poids moyen d’un procédé de remplissage
Supposons que pour un échantillon de n = 47 pots, on a  = 138,2 g. L’expression 5.1.1.3 suggère alors l’intervalle dont les extrémités sont
= 138,2 g. L’expression 5.1.1.3 suggère alors l’intervalle dont les extrémités sont
138,2 g 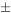 0,3 g
0,3 g
(c’est-à-dire l’intervalle de 137,9 g à 138,5 g) correspond à l’intervalle de confiance de 80 % pour le poids de remplissage moyen du processus.
Ce n’est pas difficile de généraliser la logique qui a conduit à l’expression 5.1.1.3. Chaque fois qu’un modèle iid est approprié pour les éléments d’un grand échantillon, le théorème central limite implique que la moyenne de l’échantillon  est approximativement normale avec une moyenne µ et un écart-type de σ/√n. Ainsi, si pour p > 0,5, z est le quantile p de la distribution normale standard, la probabilité que
est approximativement normale avec une moyenne µ et un écart-type de σ/√n. Ainsi, si pour p > 0,5, z est le quantile p de la distribution normale standard, la probabilité que
5.1.1.4 <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/23e5ea2cfa26dee2d7c3778c4b18b463.png » alt= »\mu-z \frac{\sigma}{\sqrt{n}}<\bar{x}<\mu+z \frac{\sigma}{\sqrt{n}} » title= »\mu-z \frac{\sigma}{\sqrt{n}}<\bar{x}
vaut approximativement 1 − 2(1 − p). Mais l’inégalité 5.1.1.4 peut être réécrite comme suit :
5.1.1.5 <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/0f6a0d4dd99aa1e750fbd9552ca6389c.png » alt= »\bar{x}-z \frac{\sigma}{\sqrt{n}}<\mu<\bar{x}+z \frac{\sigma}{\sqrt{n}} » title= »\bar{x}-z \frac{\sigma}{\sqrt{n}}<\mu
et considérée comme l’éventualité que l’intervalle aléatoire avec les extrémités
EXPRESSION 5.1.1.6 Bornes de l’intervalle de confiance de 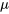 (
(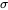 connu, n = grand)
connu, n = grand)
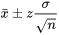
comprend la moyenne µ inconnue. Ainsi, un intervalle avec les extrémités 5.1.1.6 est un intervalle de confiance approximatif pour µ, avec un niveau de confiance 1 − 2(1 − p).
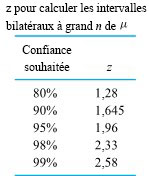
Dans une application, le z de l’équation 5.1.1.6 est choisi de sorte que la probabilité normale réduite entre -z et z corresponde à un niveau de confiance souhaité. La table A1.1 de l’annexe (Table de probabilités de la loi normale centrée réduite) peut être utilisée pour valider les entrées du tableau 5.1.1.1. (Ce tableau donne les valeurs de z à utiliser dans l’expression 5.1.1.6 pour quelques niveaux de confiance courants).
Exemple 5.1.1.2 Intervalle de confiance pour l’écart moyen par rapport à la valeur nominale dans une opération de meulage
Dib, Smith et Thompson ont étudié un processus de meulage utilisé dans la reconstruction des moteurs automobiles. La variabilité naturelle à court terme associée aux diamètres des manetons des vilebrequins de moteurs meulés par le procédé était de l’ordre de σ = 0,7 × 10-4 po. Supposons que le processus de meulage des manetons puisse être considéré comme physiquement stable sur des séries de 50 manetons ou moins. Si 32 diamètres de maneton consécutifs présentent un écart moyen par rapport à la valeur nominale de  =−0,16 × 10−4 po, on peut utiliser l’expression 5.1.1.6 pour établir un intervalle de confiance pour l’écart moyen du processus actuel par rapport à la valeur nominale. Considérons un niveau de confiance de 95 %. En consultant le tableau 5.1.1.1 (ou en réalisant autrement que le quantile p = 0,975 de la distribution normale standard correspond à 1,96), on utilise z = 1,96 dans l’équation 5.1.1.6. (On utilise p = 0,975 puisque 0,95 = 1 – 2(1 – 0,975).) Ainsi, l’intervalle de confiance de 95 % pour l’écart moyen du procédé actuel par rapport au diamètre nominal du maneton a pour bornes
=−0,16 × 10−4 po, on peut utiliser l’expression 5.1.1.6 pour établir un intervalle de confiance pour l’écart moyen du processus actuel par rapport à la valeur nominale. Considérons un niveau de confiance de 95 %. En consultant le tableau 5.1.1.1 (ou en réalisant autrement que le quantile p = 0,975 de la distribution normale standard correspond à 1,96), on utilise z = 1,96 dans l’équation 5.1.1.6. (On utilise p = 0,975 puisque 0,95 = 1 – 2(1 – 0,975).) Ainsi, l’intervalle de confiance de 95 % pour l’écart moyen du procédé actuel par rapport au diamètre nominal du maneton a pour bornes
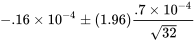
soit
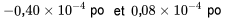
Un intervalle comme celui-ci pourrait avoir une importance technique pour déterminer la pertinence de procéder à un ajustement de l’objectif du processus. L’intervalle comprend à la fois des valeurs positives et négatives. Par conséquent, même si  < 0, les informations dont nous disposons ne sont pas suffisamment précises pour nous permettre de déterminer avec certitude dans quelle direction le processus de meulage doit être ajusté. Ces données, jumelées au fait que les ajustements potentiels de la machine sont probablement plus grossiers que l’erreur d’ajustement la plus probable
< 0, les informations dont nous disposons ne sont pas suffisamment précises pour nous permettre de déterminer avec certitude dans quelle direction le processus de meulage doit être ajusté. Ces données, jumelées au fait que les ajustements potentiels de la machine sont probablement plus grossiers que l’erreur d’ajustement la plus probable  = −0,16 × 10−4 po, suggère fortement de ne pas modifier l’objectif du processus.
= −0,16 × 10−4 po, suggère fortement de ne pas modifier l’objectif du processus.
Intervalle de confidence généralement applicable pour 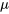 (n = grand)
(n = grand)
Bien que l’expression 5.1.1.6 fournisse un intervalle de confiance mathématiquement correct, la présence de σ limite fortement son utilité pratique. Il est inhabituel de devoir estimer une moyenne µ en connaissant déjà σ (qu’on pourrait alors insérer dans une équation). Ces situations se produisent principalement dans des situations de fabrication comme celles des exemples 5.1.1.1 et 5.1.1.2. Une expérience passée considérable peut parfois donner une valeur raisonnable à σ, tandis que les dérives des processus physiques au fil du temps peuvent remettre en question la valeur actuelle de µ.
Heureusement, on peut modifier le raisonnement qui a conduit à l’expression 5.1.1.1 pour obtenir une équation d’intervalle de confiance pour µ qui ne dépend que des caractéristiques de l’échantillon. L’argument conduisant à l’expression 5.1.1.6 repose sur le fait que pour des n grands,  est approximativement normale avec une moyenne µ et un écart-type σ/√n. Autrement dit, la variable
est approximativement normale avec une moyenne µ et un écart-type σ/√n. Autrement dit, la variable
5.1.1.7
est approximativement normale réduite. La présence de σ dans l’équation 5.1.1.7 est ce qui conduit à sa présence dans l’expression 5.1.1.6 pour l’intervalle de confiance. Mais une légère généralisation du théorème central limite garantit que si n est grand,
5.1.1.8
est également approximativement normale réduite. Cette fois-ci, il n’y a pas de σ.
En partant du fait que (lorsqu’un modèle iid pour les observations est approprié et que n est grand) la variable 5.1.1.8 est approximativement normale réduite, le raisonnement est le même que précédemment. Pour un z positif,
-z < 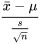 < z
< z
équivaut à
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/b932991fa9407c4d40d2e0aeec54cc28.png » alt= »\mu-z \frac{S}{\sqrt{n}}<\bar{x}<\mu+z \frac{S}{\sqrt{n}} » title= »\mu-z \frac{S}{\sqrt{n}}<\bar{x}
qui à son tour, équivaut à
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/577f2908f08263064a6791ad9a634f85.png » alt= »\bar{x}-z \frac{S}{\sqrt{n}}<\mu<\bar{x}+z \frac{S}{\sqrt{n}} » title= »\bar{x}-z \frac{S}{\sqrt{n}}<\mu
Ainsi, l’intervalle dont le centre aléatoire est  et la longueur aléatoire est 2zs/√n – autrement dit, avec des bornes aléatoires
et la longueur aléatoire est 2zs/√n – autrement dit, avec des bornes aléatoires
EXPRESSION 5.1.1.9 Intervalle de confiance pour 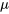 (n = grand)
(n = grand)
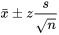
peut être utilisé comme intervalle de confiance approximatif de µ. La valeur de z doit être choisie de sorte que la probabilité normale standard entre -z et z corresponde au niveau de confiance voulu.
Example 5.1.1.3 Couples de rupture et défaillances des disques durs
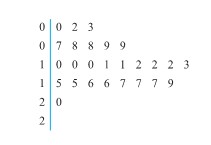
Dans l’article « The Case of the Derailed Disk Drives » (Mechanical Engineering, 1988), F. Willett évoque une étude réalisée pour isoler la cause de la « défaillance du code de clignotement A » dans un modèle de disque dur Winchester. Les données de cet article ont été reprises à la figure 5.1.1.2, qui présente les couples de rupture (po oz) nécessaires pour desserrer le dispositif d’interruption du lecteur sur l’arbre du moteur pas à pas pour 26 disques durs renvoyés au fabricant pour une défaillance du code de clignotement A. Pour ces données,  = 11,5 po oz et s = 5,1 po oz.
= 11,5 po oz et s = 5,1 po oz.
Si l’on considère que les disques durs qui ont produit les données de la figure 5.1.1.2 représentent la population des lecteurs sujets à une défaillance du code de clignotement A, il semble raisonnable d’utiliser un modèle iid et l’expression 5.1.1.9 pour estimer le couple de rupture moyen de la population. On choisit d’utiliser un intervalle de confiance de 90 % pour µ; le tableau 5.1.1.1 donne alors z = 1.645.En utilisant l’expression 5.1.1.9, on obtient les bornes
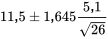
(c’est-à-dire 9,9 et 13,1 po oz).
L’intervalle montre que le couple de rupture moyen pour les lecteurs présentant une défaillance du code de clignotement A était nettement inférieur à la valeur cible de 33,5 po oz fixée par l’usine, ce qui a été essentiel pour trouver et éliminer un défaut de conception dans les lecteurs.
Quelques commentaires sur les intervalles de confiance
Les expressions 5.1.1.6 et 5.1.1.9 ont été utilisées pour établir des déclarations de confiance du type « µ est compris entre a et b ». Mais souvent, une déclaration telle que « µ est au moins égal à c » ou « µ n’est pas supérieur à d » aurait une plus grande valeur pratique. Par exemple, un.e ingénieur.e automobile pourrait déclarer: « L’émission moyenne de monoxyde d’azote pour ce moteur est au maximum de 5 ppm ». Un.e ingénieur.e en génie civil peut aussi vouloir faire une déclaration telle que « la résistance moyenne à la compression des échantillons de ce type de béton est d’au moins 4 188 psi ». En d’autres termes, les problèmes pratiques d’ingénierie se prête parfois mieux à des intervalles de confiance unilatéraux.
Établissement d’intervalles de confiance unilatérauxL’élaboration de formules pour les intervalles de confiance unilatéraux ne pose pas de réel problème. Si vous disposez d’une formule bilatérale viable, il suffit de faire ce qui suit :
1. Remplacer la limite inférieure par −∞ ou la limite supérieure par +∞.
2. Ajuster le niveau de confiance déclaré à la hausse de manière appropriée (ce qui implique généralement
de diviser le « niveau de confiance » par 2).
Cette méthode fonctionne non seulement avec les expressions 5.1.1.6 et 5.1.1.9, mais aussi avec les autres intervalles de confiance bilatéraux présentés dans cette partie.
Exemple 5.1.1.4 (suite)
Pour le couple moyen de rupture des disques durs défectueux, définissions un intervalle de confiance unilatéral à 90 % pour µ de la forme (-∞, #), avec # un nombre approprié. En d’autres termes, cherchons une limite de confiance supérieure (#) de 90 % pour µ.
Pour obtenir un intervalle de confiance unilatéral à 90 %, on part d’un intervalle de confiance bilatéral à 80 % pour µ, et on remplace la limite inférieure par -∞. Ainsi, en utilisant l’expression 5.1.1.9, la limite de confiance supérieure à 90 % pour le couple de rupture moyen est la suivante :
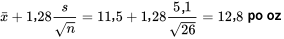
De manière équivalente, l’intervalle de confiance unilatéral à 90 % pour µ est (-∞, 12,8).
Le chiffre de 12,8 po oz est inférieur à la limite supérieure de 13,1 po oz de l’intervalle bilatéral à 90 % trouvé précédemment (et plus proche de la moyenne de l’échantillon). Dans le cas unilatéral, -∞ est déclaré comme limite inférieure, de sorte qu’il n’y a pas de risque de produire un intervalle contenant uniquement des nombres plus grands que l’inconnue µ. Il est donc possible d’utiliser une limite supérieure plus petite que celle de l’intervalle bilatéral correspondant.
Interprétation des intervalles de confiance
Un deuxième problème lié à l’application des intervalles de confiance est la compréhension correcte de la signification technique du terme confiance. Malheureusement, il est facile de se méprendre à ce sujet. Il est donc important d’exposer avec soin ce que la confiance
signifie et ne signifie pas.
Avant de sélectionner un échantillon et d’utiliser l’expression 5.1.1.6 ou 5.1.1.9, la signification d’un niveau de confiance est évidente. En choisissant un niveau de confiance (bilatéral) de 90 % et donc z = 1,645 pour l’expression 5.1.1.9, avant la sélection de l’échantillon et les calculs, « il y a environ 90 % de chances de trouver un intervalle qui comprend µ ». Sous forme de symboles, cela pourrait être exprimé comme suit :
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/b4b1dca0965666b2b65d21cdce2c71b6.png » alt= »P\left[\bar{x}-1,645 \frac{s}{\sqrt{n}}<\mu<\bar{x}+1,645 \frac{s}{\sqrt{n}}\right] \approx 0,90″ title= »P\left[\bar{x}-1,645 \frac{s}{\sqrt{n}}<\mu
Mais comment envisager un niveau de confiance après la sélection de l’échantillon? En fait, c’est là une toute autre question. Une fois les chiffres introduits dans l’expression 5.1.1.6 ou 5.1.1.9, les dés sont déjà jetés et l’intervalle numérique est soit correct, soit erroné. La difficulté pratique est que si on ne peut déterminer lequel des deux est le cas, il n’est plus logique d’associer une probabilité à l’exactitude de l’intervalle. Par exemple, cela n’aurait aucun sens d’examiner à nouveau l’intervalle bilatéral obtenu dans l’exemple 5.1.1.3 et d’essayer de dire quelque chose comme « il existe une probabilité de 90 % que µ soit compris entre 9,9 et 13,1 po oz ». µ n’est pas une variable aléatoire; il s’agit d’une quantité fixée (bien qu’inconnue) qui se situe – ou pas – entre 9,9 et 13,1. Il n’y a plus de probabilité dans la situation à discuter.
Que signifie donc que (9,9, 13,1) est un intervalle de confidence à 90 % pour µ? Qu’on le veuille ou non, l’expression « 90 % de confiance » fait davantage référence à la méthode utilisée pour obtenir l’intervalle (9,9, 13,1) qu’à l’intervalle lui-même. Pour déterminer l’intervalle, une méthodologie a été utilisée qui produirait des intervalles numériques se situant entre µ dans environ 90 % des applications répétées. Mais la validité de cet intervalle en particulier dans cette application est inconnue et n’est pas quantifiable en termes de probabilité. Une personne qui, au cours de sa vie, définit de nombreux intervalles de confiance de 90 % peut s’attendre à avoir un « taux de réussite au cours de sa vie » d’environ 90 %. Mais la validité d’une application donnée n’est généralement pas connue.
Voici un bref énoncé pour résumer ces discussions.
DÉFINITION 5.1.1.2 Interprétation des intervalles de confiance
Dire qu’un intervalle numérique (a, b) est (par exemple) un intervalle de confiance à 90 % pour un paramètre, c’est dire qu’en l’obtenant, on a appliqué des méthodes de collecte de données et de calcul qui produiraient des intervalles comprenant le paramètre dans environ 90 % des applications répétées. Le fait que l’intervalle (a, b) en question comprenne – ou pas – le paramètre est inconnu et ne peut être décrit en termes de probabilité.
On peut penser que la définition 5.1.1.2 donne une signification assez faible au niveau de la fiabilité associée aux intervalles de confiance. Néanmoins, il s’agit de l’interprétation correcte, et c’est tout ce à quoi on peut s’attendre rationnellement. Et bien que l’interprétation correcte puisse sembler peu attrayante au départ, les méthodes d’intervalle de confiance se sont révélées d’une grande utilité pratique.
Taille de l’échantillon pour estimer 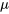
Pour conclure cette introduction aux intervalles de confiance, notons que les expressions 5.1.1.6 et 5.1.1.9 peuvent donner des réponses quantitatives rudimentaires à la question « Quelle doit être la taille de n? ». En utilisant l’expression 5.1.1.9, par exemple, si on connaît 1) le niveau de confiance souhaité, 2) l’estimation du pire cas pour l’écart-type de l’échantillon, et 3) la précision d’estimation souhaitée pour µ, il est facile de déterminer la taille de l’échantillon correspondant. Autrement dit, supposons que le niveau de confiance souhaité dicte la valeur de z utilisée dans l’expression 5.1.1.9, que s est la valeur probable du pire cas pour l’écart type de l’échantillon, et qu’on souhaite avoir une ou des limites de confiance de la forme  ±
±  . Soit
. Soit
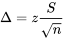
On isole n, ce qui donne :
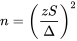
Exemple 5.1.1.3 suite
Supposons que, dans le cas du problème des disque durs, les ingénieur.e.s veulent approfondir l’analyse des données de la figure 5.1.1.2 en procédant à des essais sur de nouveaux lecteurs après les avoir soumis à des conditions de température accélérée (élevée) dans le but de comprendre le mécanisme à l’origine de la création des faibles couples de rupture. Supposons en outre que le couple de rupture moyen des lecteurs soumis à des contraintes de température doit être estimé avec un intervalle de confiance bilatéral de 95 % et que la variabilité du couple attendue n’excède pas la valeur s = 5,1 po oz obtenue à partir des lecteurs retournés. On souhaite obtenir une précision d’estimation de ±1 po oz. En utilisant la partie ± de l’expression 5.1.1.9 et en se reportant au tableau 5.1.1.1, l’exigence est la suivante :
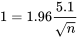
En isolant n, on obtient :
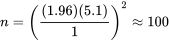
Il faudrait donc étudier n = 100 disques durs soumis à des contraintes de température. Si ce nombre n’est pas pratique, les calculs indiquent au moins que le fait de descendre en dessous de cette taille d’échantillon entraînera une réduction de la confiance ou de la précision associée à l’intervalle final (à moins que la variabilité associée aux nouveaux disques soit inférieure à celle des disques retournés).
Il y a deux raisons pour lesquelles les calculs effectués dans l’exemple précédent ne constituent pas une réponse absolue à la question de la taille de l’échantillon. La première, c’est que leur validité dépend de la justesse de s, l’estimation de l’écart-type de l’échantillon. Si s est sous-estimé, n sera trop petit. (De même, si on surestime s par excès de prudence, l’échantillon sera inutilement grand.) La deuxième, c’est que l’expression 5.1.1.9 repose sur l’hypothèse d’un grand échantillon. Si les calculs donnent un n inférieur à environ 25 ou 30, il faudra augmenter la taille pour garantir la validité de l’expression 5.1.1.9.