4.2.1 Distributions conjointes
Description des variables aléatoires discrètes conjointes
 et
et  est une fonction non-négative
est une fonction non-négative 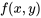 , qui calcule la probabilité que
, qui calcule la probabilité que prenne la valeur
prenne la valeur 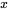 et que
et que  prenne la valeur
prenne la valeur 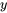 (simultanément). Autrement dit,
(simultanément). Autrement dit,![f(x, y)=P[X=x \text { et } Y=y] f(x, y)=P[X=x \text { et } Y=y]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/0b98ddcec1358e23f0edde7603a4572b.png)
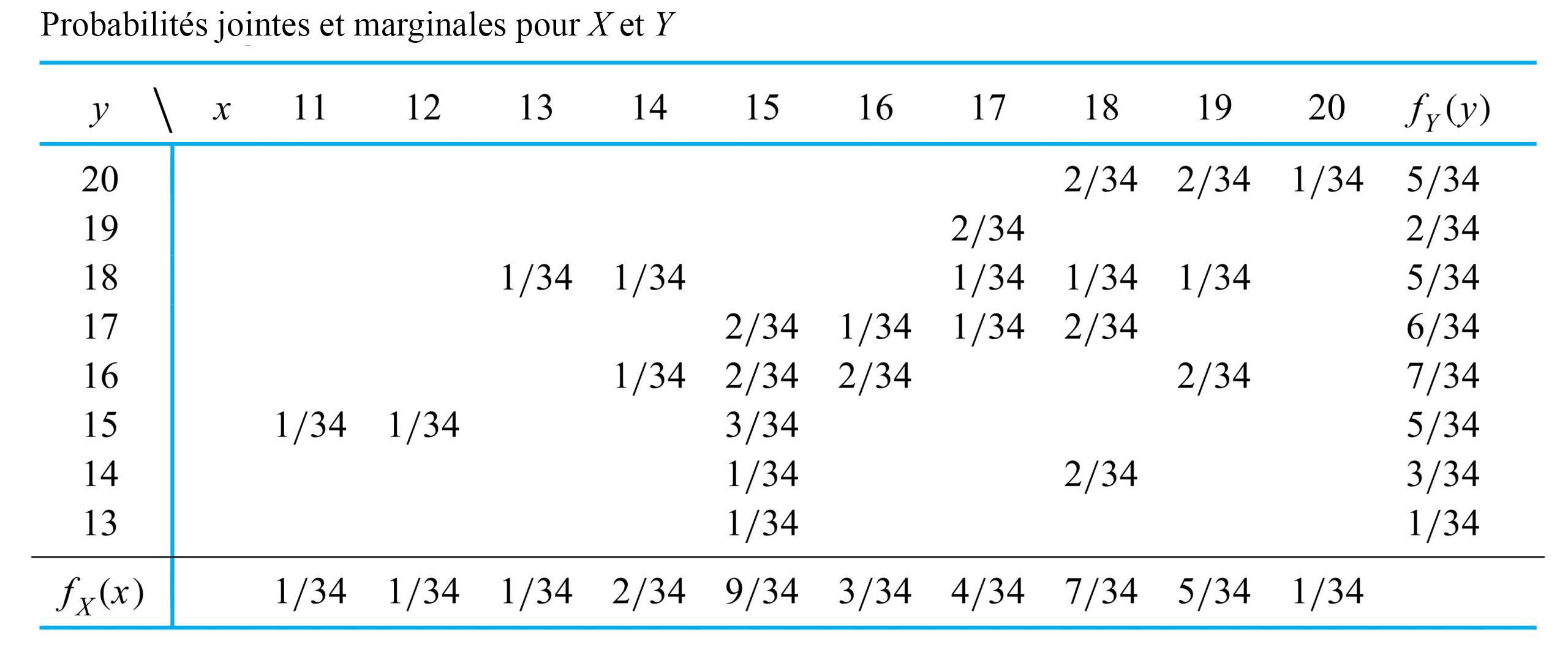
Exemple 4.2.1.1. Distribution de probabilité conjointe de deux couples de boulons
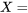 le prochain couple enregistré pour le boulon 3
le prochain couple enregistré pour le boulon 3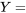 le prochain couple enregistré pour le boulon 4
le prochain couple enregistré pour le boulon 4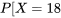 et
et ![Y=18] Y=18]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/7b60878193a2a3ebd3d9c6686c22d985.png) pourrait être
pourrait être 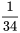 , la fréquence relative de cette paire dans l’ensemble de données. De même, les valeurs
, la fréquence relative de cette paire dans l’ensemble de données. De même, les valeurs![\begin{aligned}& P[X=18 \text { et } Y=17]=\frac{2 }{ 34} \\& P[X=14 \text { et } Y=9]=0\end{aligned} \begin{aligned}& P[X=18 \text { et } Y=17]=\frac{2 }{ 34} \\& P[X=14 \text { et } Y=9]=0\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/f043af9dc4c47fbf28ee933f1241c4d0.png)
 et de
et de  , ces probabilités peuvent être rassemblées de manière pratique dans un tableau à deux dimensions spécifiant une fonction de probabilité conjointe pour
, ces probabilités peuvent être rassemblées de manière pratique dans un tableau à deux dimensions spécifiant une fonction de probabilité conjointe pour  et
et  . Cette fonction est illustrée dans le tableau 4.2.1.1. (Pour alléger le tableau, les entrées « 0 » ont été laissées en blanc).
. Cette fonction est illustrée dans le tableau 4.2.1.1. (Pour alléger le tableau, les entrées « 0 » ont été laissées en blanc).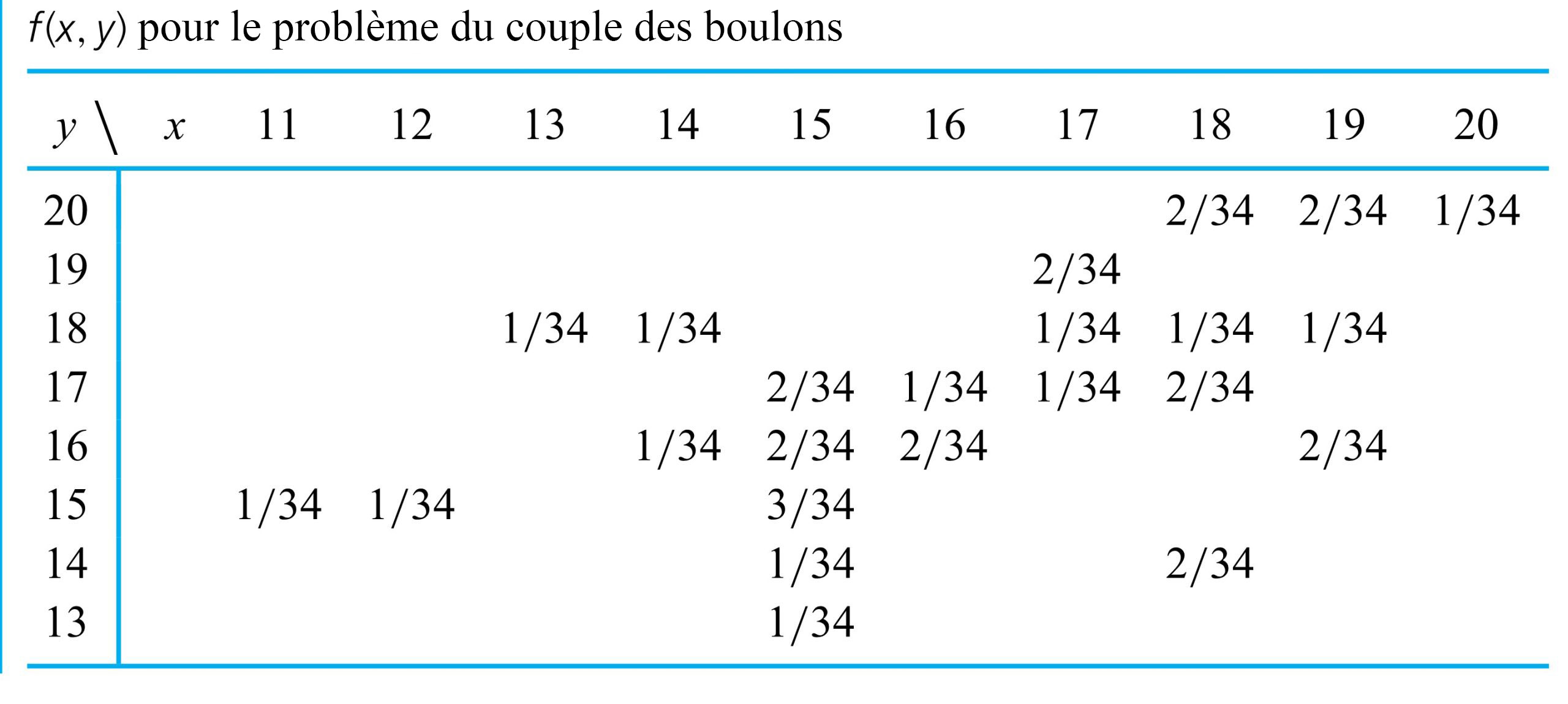
Propriétés d'une fonction de probabilité conjointe pour  et
et 
La fonction de probabilité présentée sous forme de table dans le tableau 4.2.1.1 possède deux propriétés requises pour qu’elle soit mathématiquement cohérente : les valeurs de 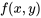 sont toutes comprises dans l’intervalle
sont toutes comprises dans l’intervalle ![[0,1] [0,1]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/344478f605e0a63e4fb539fbfc216ad1.png) , et leur somme vaut 1. Pour obtenir la probabilité d’une configuration d’intérêt
, et leur somme vaut 1. Pour obtenir la probabilité d’une configuration d’intérêt 
 donnée, il suffit d’additionner les valeurs correspondantes de
donnée, il suffit d’additionner les valeurs correspondantes de 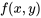 .
.
Exemple 4.2.1.2 Exemple de couples de boulons (suite)
![\begin{aligned}& P[X\geq Y], \\& P[|X-Y|\leq 1], \\& \text { et } P[X=17]\end{aligned} \begin{aligned}& P[X\geq Y], \\& P[|X-Y|\leq 1], \\& \text { et } P[X=17]\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/3a431cdee21c01d58bfeb2e20efe60e4.png)
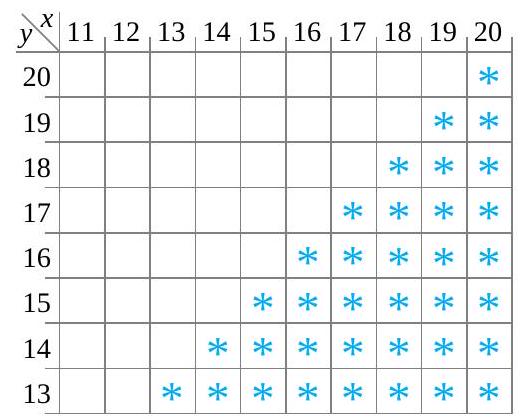
![P[X \geq Y] P[X \geq Y]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/af46a0fb553ac0a80758e888cfaa850b.png) , la probabilité que le couple du boulon 3 soit au moins aussi important que le couple du boulon 4. La figure 4.2.1.1 indique par des astérisques les combinaisons possibles de
, la probabilité que le couple du boulon 3 soit au moins aussi important que le couple du boulon 4. La figure 4.2.1.1 indique par des astérisques les combinaisons possibles de 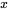 et
et 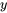 qui satisfont ce critère, En se référant au tableau 4.2.1.1 et en additionnant les entrées correspondant aux cellules contenant des astérisques, on obtient :
qui satisfont ce critère, En se référant au tableau 4.2.1.1 et en additionnant les entrées correspondant aux cellules contenant des astérisques, on obtient :![\begin{aligned}P[X \geq Y]= & f(15,13)+f(15,14)+f(15,15)+f(16,16) \\& +f(17,17)+f(18,14)+f(18,17)+f(18,18) \\& +f(19,16)+f(19,18)+f(20,20) \\= & \frac{ 1}{ 34}+\frac{ 1}{ 34}+\frac{ 3}{ 34}+\frac{ 2}{ 34}+\cdots+\frac{ 1}{ 34}=\frac{ 17}{ 34}\end{aligned} \begin{aligned}P[X \geq Y]= & f(15,13)+f(15,14)+f(15,15)+f(16,16) \\& +f(17,17)+f(18,14)+f(18,17)+f(18,18) \\& +f(19,16)+f(19,18)+f(20,20) \\= & \frac{ 1}{ 34}+\frac{ 1}{ 34}+\frac{ 3}{ 34}+\frac{ 2}{ 34}+\cdots+\frac{ 1}{ 34}=\frac{ 17}{ 34}\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e8700d378546578de7dab9beaf219426.png)
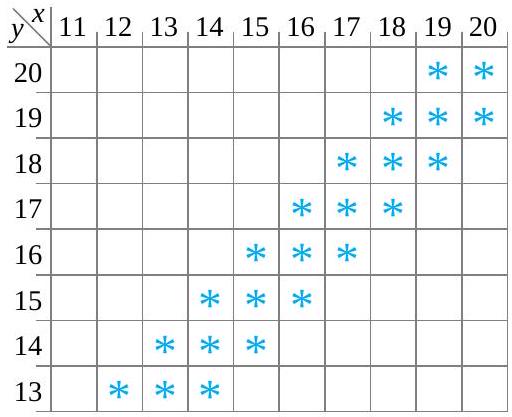
![P[|X-Y| \leq 1] P[|X-Y| \leq 1]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e863f7444d8179376e25d920e88fbd40.png) -la probabilité que les couples des boulons 3 et 4 se situent à
-la probabilité que les couples des boulons 3 et 4 se situent à 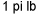 l’un de l’autre. La figure 4.2.1.2 illustre les combinaisons de
l’un de l’autre. La figure 4.2.1.2 illustre les combinaisons de 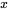 et
et 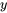 avec une différence absolue de 0 ou 1. Ensuite, on additionne les probabilités correspondant à ces combinaisons :
avec une différence absolue de 0 ou 1. Ensuite, on additionne les probabilités correspondant à ces combinaisons :![\begin{aligned}P[|X-Y| \leq 1]= & f(15,14)+f(15,15)+f(15,16)+f(16,16) \\& +f(16,17)+f(17,17)+f(17,18)+f(18,17) \\& +f(18,18)+f(19,18)+f(19,20)+f(20,20)=\frac{ 18}{ 34}\end{aligned} \begin{aligned}P[|X-Y| \leq 1]= & f(15,14)+f(15,15)+f(15,16)+f(16,16) \\& +f(16,17)+f(17,17)+f(17,18)+f(18,17) \\& +f(18,18)+f(19,18)+f(19,20)+f(20,20)=\frac{ 18}{ 34}\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/65e181c2f20553b81748bdc1a694cbcd.png)
.
![P[X=17] P[X=17]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/0912a53b69eb7eb10e46c1f59352e883.png) , la probabilité que le couple mesuré sur le boulon 3 soit
, la probabilité que le couple mesuré sur le boulon 3 soit  , s’obtient en additionnant la colonne
, s’obtient en additionnant la colonne 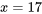 dans le tableau 4.2.1.1. Autrement dit,
dans le tableau 4.2.1.1. Autrement dit,![\begin{aligned} P[X=17] & =f(17,17)+f(17,18)+f(17,19) \\ & =\frac{ 1}{ 34}+\frac{ 1}{ 34}+\frac{ 2}{ 34} \\ & =\frac{ 4}{ 34} \end{aligned} \begin{aligned} P[X=17] & =f(17,17)+f(17,18)+f(17,19) \\ & =\frac{ 1}{ 34}+\frac{ 1}{ 34}+\frac{ 2}{ 34} \\ & =\frac{ 4}{ 34} \end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/152ecf42295f0efb7bc4bd56de294bf7.png)
Obtenir une fonction de probabilité marginale à partir d'une fonction de probabilités conjointes à deux variables
 pour obtenir les valeurs de la fonction de probabilité de
pour obtenir les valeurs de la fonction de probabilité de 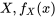 . On peut également additionner les lignes du même tableau pour obtenir les valeurs de la fonction de probabilité de
. On peut également additionner les lignes du même tableau pour obtenir les valeurs de la fonction de probabilité de 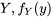 . On peut alors inscrire ces sommes dans les marges du tableau à double entrée, d’où l’appellation « distributions marginales ». L’encadré qui suit définit la terminologie utilisée dans le cas d’un problème à deux variables discrètes.
. On peut alors inscrire ces sommes dans les marges du tableau à double entrée, d’où l’appellation « distributions marginales ». L’encadré qui suit définit la terminologie utilisée dans le cas d’un problème à deux variables discrètes. et
et  obéissant à une fonction de probabilité conjointe
obéissant à une fonction de probabilité conjointe 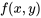 sont désignées sous le terme fonctions de probabilité marginale. Elles sont obtenues en additionnant les valeurs de
sont désignées sous le terme fonctions de probabilité marginale. Elles sont obtenues en additionnant les valeurs de 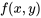 avec toutes les valeurs possibles de l’autre variable. Autrement dit, la fonction de probabilité marginale de
avec toutes les valeurs possibles de l’autre variable. Autrement dit, la fonction de probabilité marginale de  est
est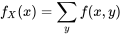
 est
est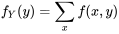
Example 4.2.1.3, suite.
Le tableau 4.2.1.2 est une copie du tableau 4.2.1.1, auquel on a ajouté les probabilités marginales de  et
et  . En séparant les marges du tableau à double entrée, on obtient des tableaux de probabilités marginales dans le format habituel. Par exemple, la fonction de probabilité marginale de
. En séparant les marges du tableau à double entrée, on obtient des tableaux de probabilités marginales dans le format habituel. Par exemple, la fonction de probabilité marginale de  est présentée séparément dans le tableau 4.2.1.3 .
est présentée séparément dans le tableau 4.2.1.3 .
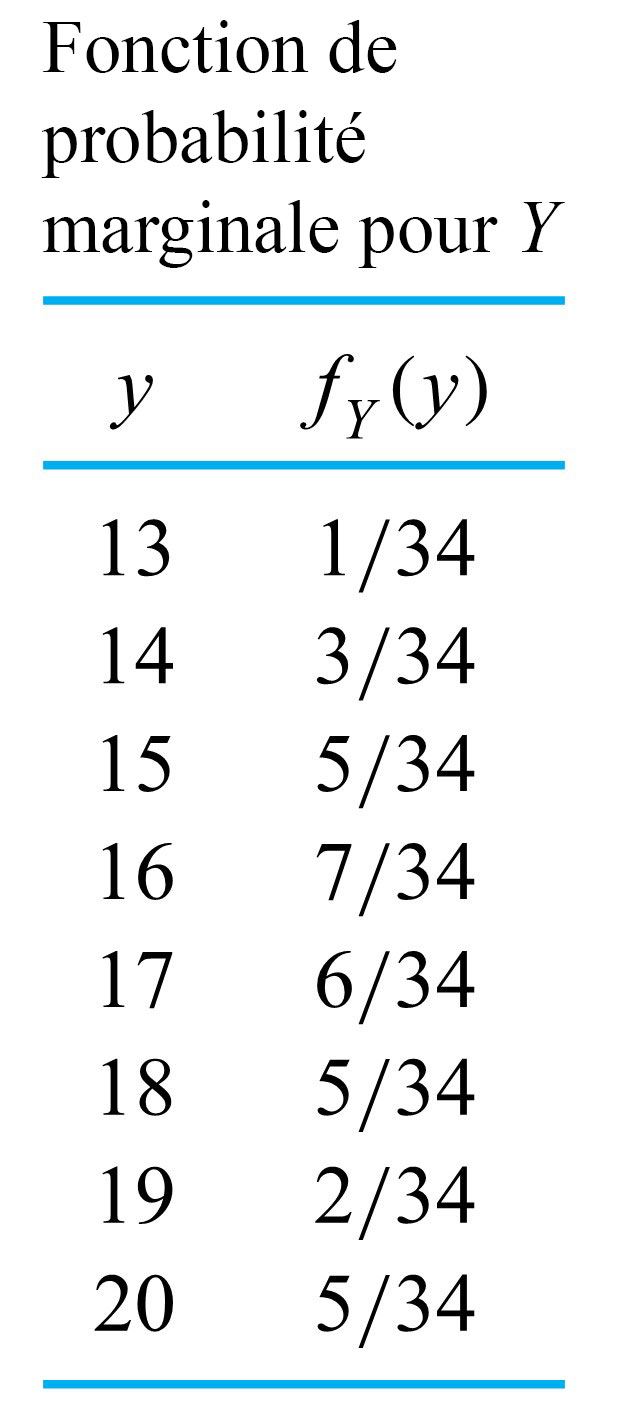
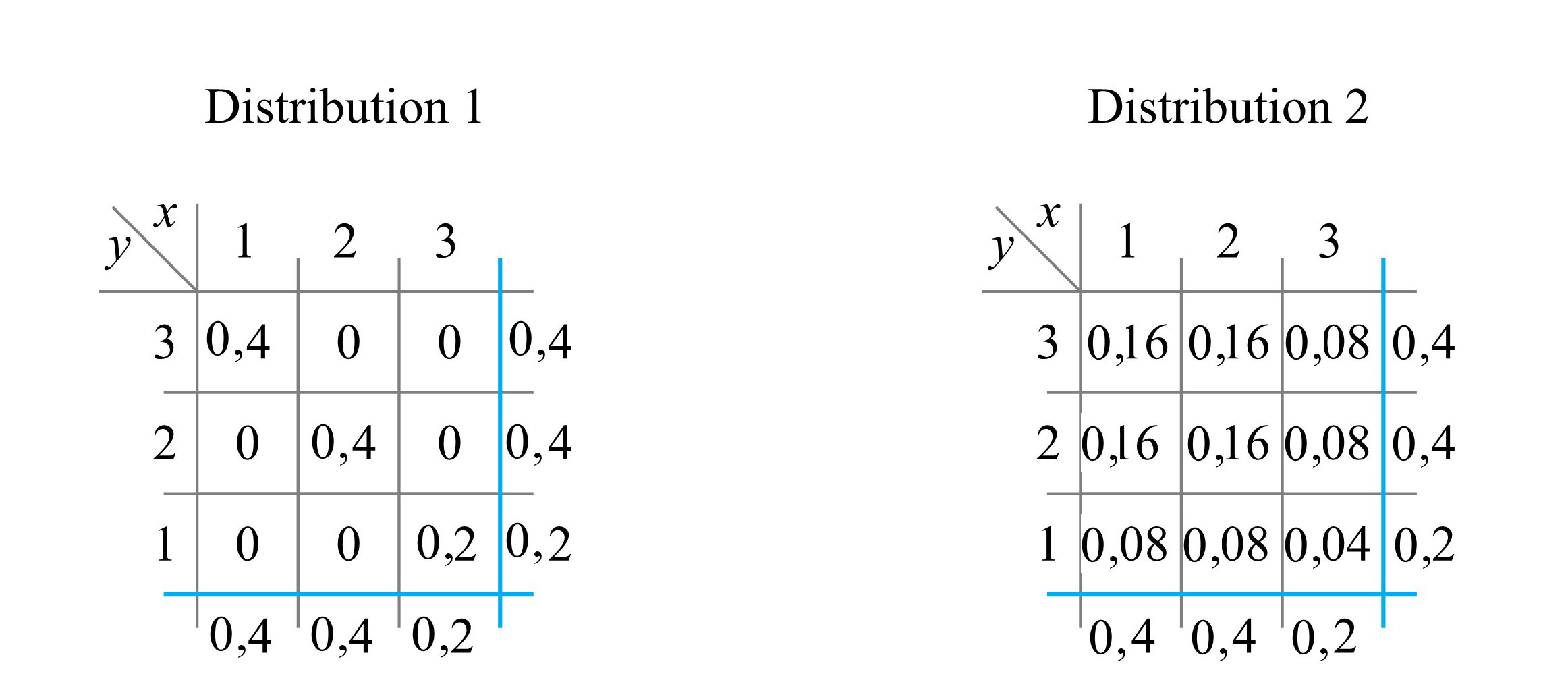
L'obtention de fonctions de probabilité marginales à partir de fonctions de probabilité conjointes soulève la question logique de savoir si le processus peut être inversé. Autrement dit, si 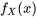 et
et 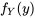 sont connues, y a-t-il alors une seule option pour
sont connues, y a-t-il alors une seule option pour 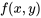 ? De fait, non. La figure 4.2.1.3 montre deux distributions conjointes à deux variables très différentes qui possèdent néanmoins les mêmes distributions marginales. La différence marquée entre les distributions de la figure 4.2.1.3 est liée au comportement conjoint, plutôt qu'individuel, de
? De fait, non. La figure 4.2.1.3 montre deux distributions conjointes à deux variables très différentes qui possèdent néanmoins les mêmes distributions marginales. La différence marquée entre les distributions de la figure 4.2.1.3 est liée au comportement conjoint, plutôt qu'individuel, de  et de
et de  .
.