4.1.4 Distribution normale réduite
Distribution normale réduite
L’utilisation de tables pour évaluer les probabilités normales repose sur la relation suivante : si X est distribuée normalement avec une moyenne µ et une variance σ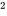
, alors
EXPRESSION 4.1.4.1.
![P[a \leq X \leq b]=\int_a^b \frac{ 1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2} d x=\int_{(a-\mu) / \sigma}^{(b-\mu) / \sigma} \frac{ 1}{\sqrt{2 \pi}} e^{-z^2 / 2} d z](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/7d7d2902c84523e28fb1268b52141fbd.png "P[a \leq X \leq b]=\int_a^b \frac{ 1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2} d x=\int_{(a-\mu) / \sigma}^{(b-\mu) / \sigma} \frac{ 1}{\sqrt{2 \pi}} e^{-z^2 / 2} d z")
où la seconde inégalité est obtenue par un changement de variable :
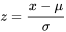
La cote z est une valeur normalisée mesurée en unités de l’écart-type. Par exemple, si la moyenne d’une distribution normale est de 5 et que l’écart-type est de 2, la valeur 11 se situe à trois écarts-types au-dessus (ou à droite) de la moyenne. Le calcul est effectué comme suit: x = μ + (z)(σ) = 5 + (3)(2) = 11, et la cote z est égale à trois : z = (11-5)/2 = 3. La cote z indique de combien d’écarts-types la valeur x est supérieure (à droite) ou inférieure (à gauche) à la moyenne μ. Les valeurs de x supérieures à la moyenne ont une cote z positive, tandis que les valeurs de x inférieures à la moyenne ont une cote z négative. Si x est égal à la moyenne, alors x a une cote z de 0.
L’équation 4.1.4.1 implique une intégrale de la densité normale avec µ = 0 et σ = 1. Le changement de variable 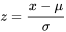z=\frac{x-\mu}{\sigma} produit la distribution Z ~ N(0,1). Cela signifie que la valeur x dans l’équation donnée provient d’une distribution normale avec une moyenne de 0 et un écart-type de 1. Autrement dit, toutes les probabilités normales peuvent être réduites à cette distribution normale spéciale. Ainsi, la distribution normale réduite est une distribution normale des valeurs normalisées à l’aide des cotes z.
DÉFINITION 4.1.4.2. DISTRIBUTION NORMALE RÉDUITE
EXPRESSION 4.1.4.2.
La distribution normale avec µ = 0 et σ = 1 est appelée distribution normale réduite.
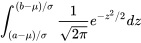
Cote z d’une valeur x d’une variable aléatoire normale (µ, σ)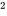
L’expression 4.1.4.2 montre comment utiliser la fonction de probabilité cumulative normale réduite pour calculer des probabilités normales générales. Pour une variable X normale,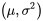 
et une valeur x associée à X on obtient la cote Z comme suit :
EXPRESSION 4.1.4.3.
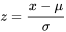
Ensuite, on consulte la table normale réduite en utilisant z à la place de x.
Relation entre les probabilités normales (µ, σ) et les probabilités normales réduites : probabilité normale réduite cumulative
La relation entre les probabilités normales (µ, σ) et les probabilités normales réduite est illustrée à la figure 4.1.4.1
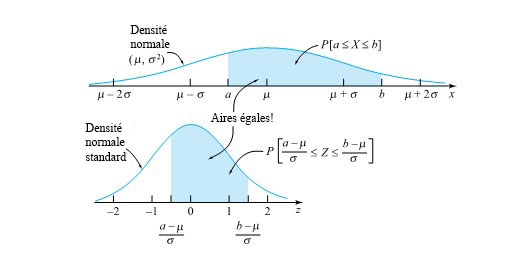
les probabilités normales réduites.
Une fois que l’on a compris que les probabilités de toutes les distributions normales peuvent être obtenues en tabulant les probabilités de la distribution normale réduite seulement, il est relativement simple d’utiliser des techniques d’intégration numérique pour produire une table normale réduite. Dans ce texte, nous utiliserons les valeurs données dans la table A1.1 Table de probabilités de la loi normale centrée réduite, à l’annexe 1. (Il existe d’autres formats.) La table A1.1 est une table de la fonction de probabilité normale réduite cumulative. En d’autres termes, pour les valeurs z situées sur les marges de la table, les entrées dans le corps de la table correspondent à :
EXPRESSION 4.1.4.4
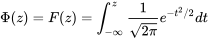
où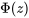 
est utilisé pour représenter la fonction de probabilité normale réduite cumulative, au lieu de la lettre F, plus générique.
Relation entre la fonction de probabilité normale réduite cumulative et la fonction quantile normale réduite
Symboliquement, avec 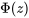, la fonction de probabilité cumulative normale réduite, et 
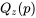, la fonction quantile normale réduite, on a :
EXPRESSION 4.1.4.5.
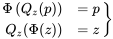
Les relations 4.1.4.5 signifient que 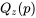et [latex]\Phi(z)[/latex] sont des fonctions inverses. (En fait, la relation
Q = F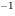
n’est pas une propriété particulière de la distribution normale réduite; cette identité tient
pour toutes les distributions continues).
EXEMPLES
Exemple 4.1.4.1. Probabilités normales réduite
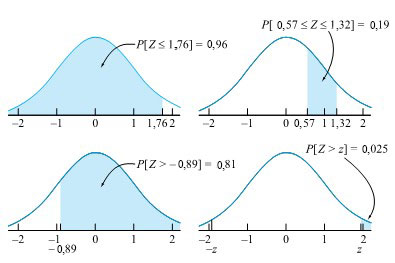
Supposons que Z soit une variable aléatoire normale réduite. Nous allons trouver des probabilités pour Z à l’aide de la table A1.1 Table des probabilités normales réduite, en annexe. En consultant la table, on constate que :
Probabilité cumulative d’une valeur de Z
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/830a0cc3769d203efead07737f8005de.png » alt= »P[Z<1,76]=\Phi(1,76)=0,96″ title= »P[Z
(La valeur de la table est de 0,9608, mais pour tenir la promesse faite à la section 3.2.3, nous l’avons arrondie à deux décimales, soit 0,96.)
Il suffit de consulter la table deux fois et de faire une soustraction pour obtenir :
Probabilité entre deux valeurs de Z : P [0,57 < Z < 1,32] = P [ Z < 1,32] − P [ Z ≤ 0,57]
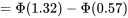
= 0,9066 − 0,7157
= 0,19
Il suffit de consulter la table une seule fois et de faire une soustraction pour obtenir une probabilité de queue droite :
Probabilité de queue droite d’une valeur Z
P [ Z > −0,89] = 1 − P [ Z ≤−0,89] = 1 − 0,1867 = 0,81
Pour ces exemples, nous avons trouvé les valeurs de Z dans les marges, puis utilisé les valeurs dans le corps de la table, mais on peut inverser ce processus. En effet, il suffit de localiser une probabilité dans le corps de la table pour trouver la cote z correspondante dans les marges. Par exemple, considérons la position d’une cote z telle que
P [−z < Z < z] = 0,95.
Il y aura donc une probabilité de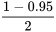 
= 0,025 que z se trouve dans la queue droite de la distribution normale
réduite. Autrement dit, on aura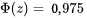 
. En repérant 0,975 dans le corps de la table, on constate que z = 1,96.
Cela revient à trouver le quantile 0,975 de la distribution normale réduite, ce qui nous permet de comprendre et de décrire les quantiles normaux réduits.
La figure 4.1.4.2 illustre tous les calculs de cet exemple.
Exemple 4.1.4.2. Poids nets des pots d’aliments pour bébés
Dans son article « Computer Assisted Net Weight Control » (Quality Progress, juin 1983), J. Fisher traite du remplissage (en grammes) de pots de nourriture. L’article présente un histogramme raisonnablement en forme de cloche des poids nets individuels des pots de nourriture pour bébé. La moyenne des valeurs représentées est d’environ 137,2 g ,et l’écart-type est d’environ 1,6 g. Le poids déclaré (ou étiqueté) sur les pots de ce produit est de 135,0 g.
Supposons qu’il soit adéquat de modéliser
W = le poids du prochain pot
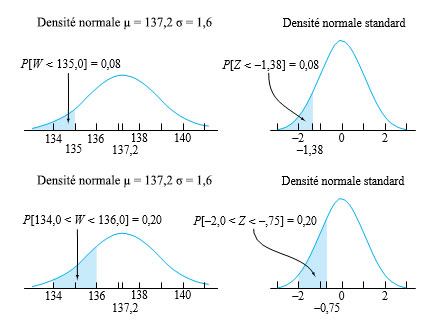
par une distribution normale avec µ = 137,2 et σ = 1,6. Supposons en outre qu’on s’intéresse à la probabilité que le prochain pot rempli soit inférieur au poids déclaré (c’est-à-dire P [W < 135,0]). En utilisant l’expression 4.1.4.3, on trouve la cote z correspondant à w = 135,0 :
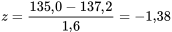
Ensuite, à l’aide de la table A1.1 en annexe, on trouve que :
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e376f007fdb232013207d123f987e4b9.png » alt= »P[W<135,0]=\Phi(-1,38)=0,08″ title= »P[W
Selon ce modèle, le risque d’obtenir un niveau de remplissage inférieur à la valeur nominale est d’environ 8 %.
En guise de deuxième exemple, considérons la probabilité que W se situe à moins d’un gramme de la valeur nominale (P [134,0 < W < 136,0]). Avec l’équation 4.1.4.3, on trouve les cotes z de w
= 134,0 et w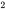
= 136,0 :
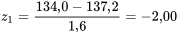
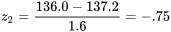
Par conséquent,
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/e82feecd2d8358abf21137e5e8f40a42.png » alt= »P[134,0 < W<136,0]=\Phi(-0,75)-\Phi(-2,00)=0,2266-0,0228=0,20″ title= »P[134,0 < W
Les deux probabilités précédentes et leurs contreparties normales réduite sont illustrées à la figure 4.1.4.3.
Exemple 4.1.4.3. Poids nets des pots de nourriture pour bébé (suite)
Pour les calculs de cet exemple, nous sommes partis des quantités du côté droit de l’équation 4.1.4.3 et des marges de la table A1.1 pour trouver les probabilités associées à diverses valeurs de W. Une variante importante de ce processus consiste à passer du corps de la table aux marges pour obtenir z, puis d’utiliser deux des trois variables du côté droit de l’équation 4.1.4.3 pour trouver la troisième.
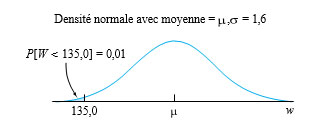
Par exemple, supposons qu’il soit facile d’ajuster la cible du processus de remplissage (c’est-à-dire la moyenne µ de W) et que l’on veuille réduire la probabilité que le prochain pot soit inférieur au poids déclaré de 135,0 à 0,01 en augmentant µ. Quelle est la valeur minimale de µ qui permet d’atteindre cet objectif (en supposant que σ constant à 1,6 g)?
La figure 4.1.4.4 montre ce qu’il faut faire : on doit choisir µ telle que w = 135,0 corresponde au quantile 0,01 de la distribution normale de moyenne µ et d’écart-type σ = 1,6. En consultant la table A1.1, il est facile de déterminer que le quantile 0,01 de la distribution normale réduite est :
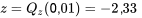
Ainsi, selon l’équation 4.1.4.3, on obtient
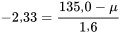
d’où µ = 138,7 g.
Il faut donc augmenter le remplissage nominal d’environ 138,7 – 137,2 = 1,5 g.
En pratique, la réduction de P [W < 135,0] s’accompagne d’une augmentation des coûts, puisque les pots contiennent en moyenne beaucoup plus que leur contenu nominal. Dans certaines applications, ce type de coût sera prohibitif. Il faudra adopter une autre approche : réduire la variation du niveau de remplissage en achetant un équipement plus précis. Selon l’équation 4.1.4.3, au lieu d’augmenter µ, on pourrait envisager de payer le coût associé à la réduction de σ. Vous pouvez vérifier qu’une réduction de σ à environ 0,94g produirait également P [W < 135,0] = 0,01 sans aucun changement dans µ.
