4.1.2 Moyenne et variance des distributions continues
Moyenne et variance des distributions continues
Le graphique de la densité de probabilité f(x) est une sorte d’histogramme idéalisé. Il offre le même type d’interprétations visuelles que celles vues pour les histogrammes de fréquence relative et les histogrammes de probabilité. En outre, il est possible de définir une moyenne et une variance pour une distribution de probabilité continue. Ces synthèses numériques s’utilisent de la même manière que la moyenne et la variances pour décrire des ensembles de données et des distributions de probabilités discrètes.
DÉFINITION 4.1.2.1. Moyenne d’une variable aléatoire continue X
EXPRESSION 4.1.2.1.
La moyenne, ou espérance mathématique, d’une variable aléatoire continue X (parfois appelée moyenne de sa distribution de probabilité) est:
.
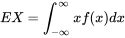Comme pour les variables aléatoires discrètes, on utilise parfois µ plutôt que E(X).
L’équation 4.1.2.1 est parfaitement plausible d’au moins deux points de vue. Premièrement, la probabilité dans un petit intervalle autour de x de longueur dx est approximativement f(x) dx. Ainsi, en multipliant par x et en additionnant, on obtient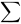
xf(x) dx, et l’équation 4.1.2.1 correspond exactement à la limite de cette somme lorsque dx tend vers zéro. Deuxièmement, en mécanique, le centre de masse d’une distribution de masse continue est de la forme donnée dans l’équation 4.1.2.1, à l’exception de la division par la masse totale, qui pour une distribution de probabilité est 1.
La « continuisation » de la formule de la variance d’une variable aléatoire discrète produit une définition de la variance d’une variable aléatoire continue.
DÉFINITION 4.1.2.2. Variance d’une variable aléatoire continue X
EXPRESSION 4.1.2.2.
La variance d’une variable aléatoire continue X (parfois appelée variance de sa distribution de probabilité) est:
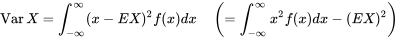
L’écart-type de X est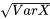 
. On utiliser souvent la notation 
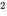à la place de Var(X), et le symbole σ est utilisé à la place de .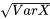