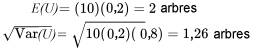3.2.5 Distribution binomiale
 ).
). qui aboutissent à un résultat de type « succès ». Autrement dit, soit la variable :
qui aboutissent à un résultat de type « succès ». Autrement dit, soit la variable : = le nombre de succès dans
= le nombre de succès dans  essais succès-échec
essais succès-échecidentiques indépendants <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/955a246b99acabb5e7c8a45cef7cc01b.png" alt="X[\latex] suit une distribution binomiale (n, p) .
DÉFINITION 3.2.5.1. Définition de la distribution binomiale La distribution binomiale [latex][/latex](n, p)" class="latex mathjax"> est une distribution de probabilité discrète avec une fonction de probabilité
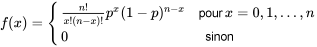
 un entier positif et <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/75d5ea78867a7472b54c906e926ba4c2.png" alt="0<p<1" title="0<p.
un entier positif et <img src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/75d5ea78867a7472b54c906e926ba4c2.png" alt="0<p<1" title="0<p. pour chaque essai produisant un succès et un facteur de
pour chaque essai produisant un succès et un facteur de  pour chaque essai produisant un échec. Le terme
pour chaque essai produisant un échec. Le terme 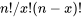 est un décompte du nombre de combinaisons dans lesquelles il est possible de voir
est un décompte du nombre de combinaisons dans lesquelles il est possible de voir 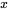 succès en
succès en  essais. Le nom distribution
essais. Le nom distribution 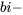 nomiale trouve son origine dans le fait que les valeurs
nomiale trouve son origine dans le fait que les valeurs 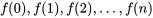 sont les termes du développement de
sont les termes du développement de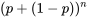
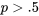 0,5" title="p>0,5" class="latex mathjax">, l’histogramme résultant est asymétrique à gauche. L’asymétrie augmente à mesure que
0,5" title="p>0,5" class="latex mathjax">, l’histogramme résultant est asymétrique à gauche. L’asymétrie augmente à mesure que  s’éloigne de 0,5 et diminue à mesure que
s’éloigne de 0,5 et diminue à mesure que  augmente. La figure 3.2.5.1 illustre quatre histogrammes de probabilité binomiale.
augmente. La figure 3.2.5.1 illustre quatre histogrammes de probabilité binomiale.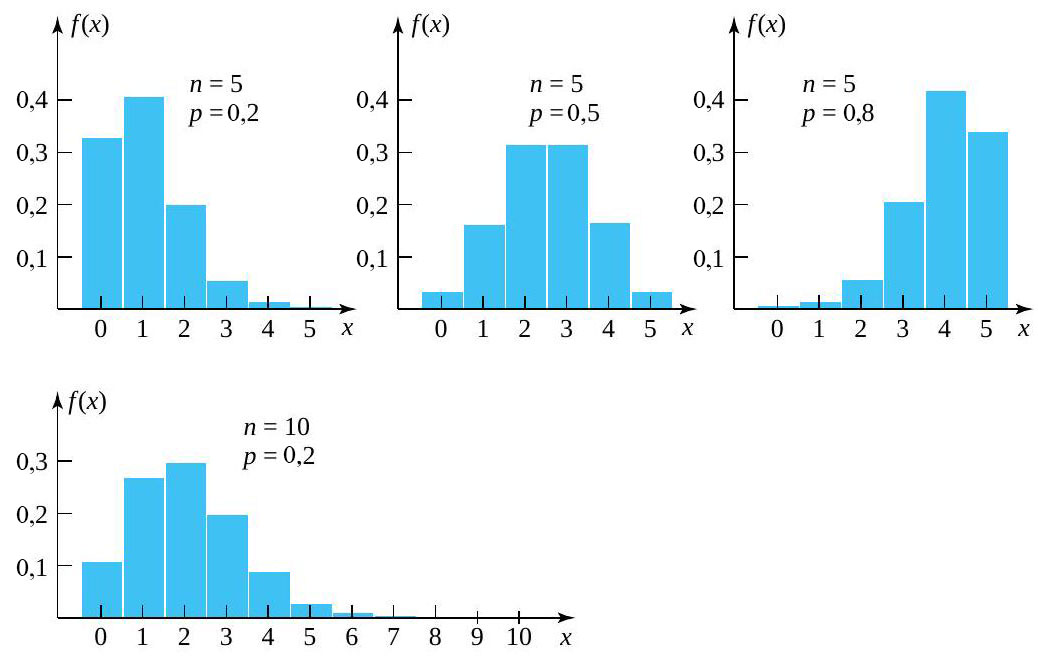
Exemple 3.2.5.1. Distribution binomiale et nombre d’arbres réusinables
 des arbres ont été classés comme « réusinables ». Supposons que
des arbres ont été classés comme « réusinables ». Supposons que  soit une probabilité crédible qu’un arbre soit réusinable. Supposons en outre qu’on inspecte
soit une probabilité crédible qu’un arbre soit réusinable. Supposons en outre qu’on inspecte  arbres et qu’on s’intéresse à la probabilité qu’au moins deux d’entre eux soient classifiés comme réusinable.
arbres et qu’on s’intéresse à la probabilité qu’au moins deux d’entre eux soient classifiés comme réusinable.
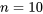 et
et 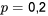 . Donc :
. Donc :![\begin{aligned}P[\text { au moins deux arbres réusinables] } & =P[U \geq 2] \\& =f(2)+f(3)+\cdots+f(10) \\& =1-(f(0)+f(1)) \\& =1-\left(\frac{10 !}{0 ! 10 !}(0,2)^{0}(0,8)^{10 }+\frac{10 !}{1 ! 9 !}(0,2)^{1 }(0,8)^{9 }\right) \\&=0,62\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/6e6263a4d29e02e515efc04bf606f376.png) \begin{aligned}P[\text { au moins deux arbres réusinables] } & =P[U \geq 2] \\& =f(2)+f(3)+\cdots+f(10) \\& =1-(f(0)+f(1)) \\& =1-\left(\frac{10 !}{0 ! 10 !}(0,2)^{0}(0,8)^{10 }+\frac{10 !}{1 ! 9 !}(0,2)^{1 }(0,8)^{9 }\right) \\&=0,62\end{aligned}
\begin{aligned}P[\text { au moins deux arbres réusinables] } & =P[U \geq 2] \\& =f(2)+f(3)+\cdots+f(10) \\& =1-(f(0)+f(1)) \\& =1-\left(\frac{10 !}{0 ! 10 !}(0,2)^{0}(0,8)^{10 }+\frac{10 !}{1 ! 9 !}(0,2)^{1 }(0,8)^{9 }\right) \\&=0,62\end{aligned}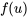 doit être égale à 1.)
doit être égale à 1.) , et le nombre 0,62 est alors peu pertinent. (L’hypothèse de l’indépendance des essais serait inappropriée dans cette situation.)
, et le nombre 0,62 est alors peu pertinent. (L’hypothèse de l’indépendance des essais serait inappropriée dans cette situation.)Distribution binomiale et échantillonnage aléatoire simple
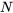 qui contient une fraction
qui contient une fraction  d’objets de type A et une fraction
d’objets de type A et une fraction  d’objets de type B. Si on sélectionne un échantillon aléatoire simple de
d’objets de type B. Si on sélectionne un échantillon aléatoire simple de  articles, alors la variable
articles, alors la variable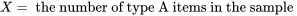
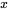 Mais si
Mais si  est petit par rapport à
est petit par rapport à 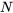 (disons, moins de
(disons, moins de 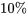 ) et que
) et que  n’est pas trop extrême (c’est-à-dire, n’est pas proche de 0 ou 1),
n’est pas trop extrême (c’est-à-dire, n’est pas proche de 0 ou 1),  suit approximativement une distribution binomiale
suit approximativement une distribution binomiale 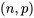 .
.Exemple 3.2.5.2. Échantillonnage aléatoire simple à partir d’un lot de pastilles d’hexamine
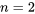 .
.
 est obtenue comme suit. Les valeurs possibles pour
est obtenue comme suit. Les valeurs possibles pour 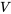 sont 0,1 et 2.
sont 0,1 et 2.![\begin{aligned}f(0)= & P[V=0] \\= & P[\text {la première pastille sélectionnée est non conforme et } \\& \text { la deuxième pastille est également non conforme}] \\f(2)= & P[V=2] \\= & P[\text {la première pastille sélectionnée est conforme et } \\& \text { la deuxième pastille sélectionnée est également conforme}] \\f(1)= & 1-(f(0)+f(2))\end{aligned} \begin{aligned}f(0)= & P[V=0] \\= & P[\text {la première pastille sélectionnée est non conforme et } \\& \text { la deuxième pastille est également non conforme}] \\f(2)= & P[V=2] \\= & P[\text {la première pastille sélectionnée est conforme et } \\& \text { la deuxième pastille sélectionnée est également conforme}] \\f(1)= & 1-(f(0)+f(2))\end{aligned}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/dddd7bf74b1653017202d626851885f8.png)
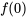 vaut
vaut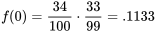
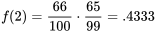
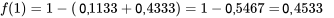
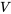 ne peut être considérée comme le résultat d’essais parfaitement indépendants. Par exemple, le fait de savoir que la première pastille sélectionnée était conforme ferait passer la probabilité que la deuxième soit également conforme de
ne peut être considérée comme le résultat d’essais parfaitement indépendants. Par exemple, le fait de savoir que la première pastille sélectionnée était conforme ferait passer la probabilité que la deuxième soit également conforme de 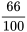 à
à 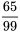 . Néanmoins, à des fins pratiques,
. Néanmoins, à des fins pratiques, 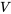 peut être considérée comme essentiellement binomiale avec
peut être considérée comme essentiellement binomiale avec 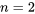 et
et 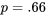 . Pour s’en convaincre, il suffit de noter que
. Pour s’en convaincre, il suffit de noter que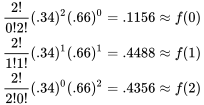
 est petit par rapport à
est petit par rapport à 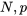 et que p n’est pas trop extrême, la distribution binomiale est une description correcte d’une variable issue d’un échantillonnage aléatoire simple.
et que p n’est pas trop extrême, la distribution binomiale est une description correcte d’une variable issue d’un échantillonnage aléatoire simple.Moyenne et variance d’une distribution binomiale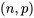
Le calcul de la moyenne et de la variance des variables aléatoires binomiales est vraiment simplifié par le fait que lorsque les formules présentées dans ce module sont utilisées avec l’expression des probabilités binomiales de l’équation 3.2.5.1, on obtient des formules simples. Soit  une variable nominale binomiale
une variable nominale binomiale 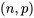 :
:
DÉFINITION 3.2.5.2. Moyenne d’une distribution binomiale (n,p)
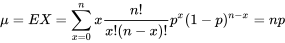
De plus,
DÉFINITION 3.2.5.3. Variance d’une distribution binomiale (n,p)
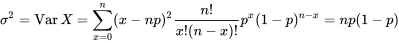
Exemple 3.2.5.3. Usinage d’arbres en acier.
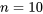 et
et 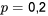 décrit adéquatement la variable
décrit adéquatement la variable