3.2.4 Moyenne ou espérance mathématique et écart-type de distributions de probabilités discrètes
Résumé des distributions de probabilités discrètes
Presque tous les outils utilisés pour décrire les distributions de fréquences relatives (empiriques) dans les modules 1 et 2 sur l’exploration, la synthèse et la visualisation des données ont des versions qui peuvent décrire des distributions (théoriques) de probabilités.
Pour une variable aléatoire discrète dont les valeurs possibles sont espacées également, l’histogramme de probabilité donne une image de la forme de la distribution de la variable. On produit cet histogramme en centrant une barre de hauteur f(x) sur chaque x possible. Les histogrammes de probabilité des variables aléatoires Z et W dans les exemples 3.2.1 sont illustrés à la figure 3B.4.1. L’interprétation de ces histogrammes de probabilité est similaire à celle des histogrammes de fréquence relative, à ceci près que l’aire représente la probabilité (théorique) au lieu des fractions (empiriques) d’ensembles de données.
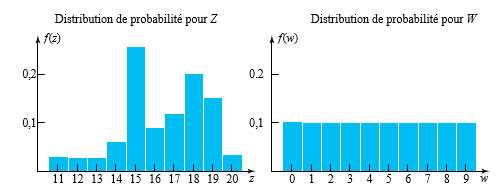
Il est utile d’avoir une notion de valeur moyenne pour une variable aléatoire discrète (ou sa distribution de probabilité).
DÉFINITION 3.2.4.1. Moyenne d’une variable aléatoire discrète
La moyenne ou espérance mathématique d’une variable aléatoire discrète X (parfois appelée moyenne de sa distribution de probabilité) est
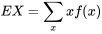
E(X) correspond à « l’espérance mathématique de X », qu’on note parfois µ.
Rappelez-vous que µ représente à la fois la moyenne d’une population et la moyenne d’une distribution de probabilité, comme nous l’avons vu avec les distributions empiriques.
Exemple 3.2.4.1. Exemple du couple des boulons (suite)
En reprenant l’exemple des couples de serrage des boulons, l’espérance mathématique (ou moyenne théorique) du prochain couple est :
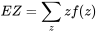
= 11(0,03) + 12(0,03) + 13(0,03) + 14(0,06) + 15(0,26) + 16(0,09) + 17(0,12) + 18(0,20) + 19(0,15) + 20(0,03)
= 16,35 ft lb
Cette valeur est essentiellement la moyenne arithmétique des couples de serrage du boulon 3 énumérés précédemment. Ce type d’accord motive l’utilisation du symbole µ, vu pour la première fois dans le module 2, comme synonyme de E(Z).
On peut interpréter la moyenne d’une distribution de probabilité discrète comme étant le point d’équilibre de la distribution, comme on l’avait fait pour la moyenne arithmétique d’un ensemble de données. Si on place des masses (ponctuelles) de valeur f(x) en des points x le long d’une droite des nombres, E(X) est le centre de masse de cette distribution.
Exemple 3.2.4.2. Exemple des numéros de série (suite)
Si on reprend l’exemple du numéro de série et la deuxième partie de la figure 3.2.4.1, pour que l’interprétation de l’espérance mathématique comme point d’équilibre tienne la route, il vaudrait mieux que E(W) soit égal à 4,5. Heureusement,
E(W) = 0(0,1) + 1(0,1) + 2(0,1) +···+8(0,1) + 9(0,1) = 45(0,1) = 4,5
Il était pratique de mesurer la dispersion d’un ensemble de données (ou de sa distribution de fréquence relative) à l’aide de la variance et de l’écart-type. Il est également utile d’avoir des notions de dispersion pour une distribution de probabilité discrète.
DÉFINITION 3.2.4.2. Variance d’une variable aléatoire discrète X
La variance d’une variable aléatoire discrète X (ou la variance de sa distribution) est :
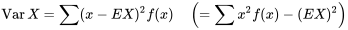
L’écart-type de X est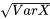 
. On utilise souvent la notation 
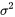à la place de Var(X), et 
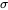à la place de .
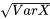La variance d’une variable aléatoire est sa distance au carré attendue (ou moyenne) par rapport au centre de sa distribution de probabilité. L’utilisation de 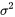pour représenter à la fois la variance d’une population et la variance d’une distribution de probabilité est motivée par les mêmes raisons que la double utilisation du symbole µ.
Exemple 3.2.4.3. Exemple du couple des boulons (suite)
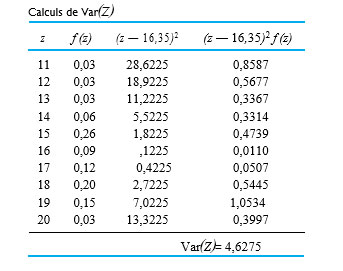
Les calculs nécessaires pour obtenir l’écart type du couple de serrage sont présentés dans le tableau 3.2.4.1. Donc :
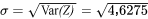= 2,15 ft lb
À l’exception d’une petite différence due aux arrondissements lors de la création du tableau 3.2.1.2, cet écart-type de la variable aléatoire Z est numériquement le même que l’écart-type de la population associé des couples du boulon 3 dans le tableau 2.1.4.1. (Encore une fois, ceci est cohérent avec l’équivalence entre la distribution de fréquence relative de la population et la distribution de probabilité de Z).
Exemple 3.2.4.4. Exemple des numéros de série (suite)
Pour illustrer l’autre méthode de calcul de la variance donnée dans la définition 3.2.4.2, essayons de calculer la variance et de l’écart type de la variable numéro de série W. Le tableau 3.2.4.2 indique le calcul de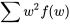 
.
D’où
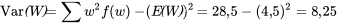
de sorte que
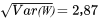
En comparant les deux histogrammes de probabilité de la figure précédente, on remarque que la distribution de W semble plus dispersée que celle de Z. Heureusement, cela se prouve mathématiquement :
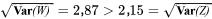2,15=\sqrt{\operatorname{Var}(Z)} » title= »\sqrt{\operatorname{Var}(W)}=2,87>2,15=\sqrt{\operatorname{Var}(Z)} » class= »latex mathjax »>