3.2.2 Fonction de distribution cumulative
Fonction de distribution cumulative
Il existe une autre façon de spécifier une distribution de probabilité discrète : la fonction de distribution cumulative (FDC, aussi appelée fonction de probabilité cumulative).
Rappelez-vous la définition d’une FDC.
![F(x)=P[X \leq x]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/02661d769255dee69404659ee6e5a9c0.png "F(x)=P[X \leq x]")
Puisque (pour les distributions discrètes) les probabilités sont calculées en additionnant les valeurs de f(x), pour une distribution discrète,
DÉFINITION 3.2.2.1. Fonction de distribution cumulative d’une variable discrète X
F(x)=\sum_{z \leq x}^{ } f(z)
La somme est calculée sur les valeurs possibles inférieures ou égales à x. Dans ce cas discret, le graphique de F(x) sera un diagramme en marches d’escalier avec des sauts situés aux valeurs possibles et de taille égale aux probabilités associées à ces valeurs.
Exemple 3.2.2.1. Retour sur le couple des boulons
Suite de l’exemple des variables de couple de la section 3.2.1
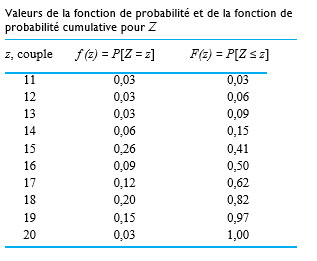
Les valeurs de la fonction de probabilité et de la fonction de probabilité cumulative pour la variable de couple Z sont indiquées dans le tableau 3.2.1.1. Les valeurs de F(z) pour d’autres z sont également faciles à obtenir. Par exemple,
F (10,7) = P [ Z ≤ 10,7] = 0
![F(16,3)=P[Z \leq 16,3]=P[Z \leq 16]=F(16)=0,50](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/9c1af41b6e51559dd079a4a47f1aafb9.png "F(16,3)=P[Z \leq 16,3]=P[Z \leq 16]=F(16)=0,50")
![F(32)=P[Z \leq 32]=1,00](https://ecampusontario.pressbooks.pub/app/uploads/sites/4171/2024/03/c83689afaf4bfd6d03d0cabb8e1a9906.png "F(32)=P[Z \leq 32]=1,00")
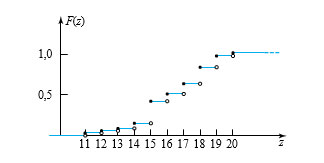
La figure 3.2.2.1 présente un diagramme de la fonction de probabilité cumulative de Z. On y voit la forme en escalier caractéristique des fonctions de probabilité cumulative des distributions discrètes.
Les informations sur une distribution discrète véhiculée par sa fonction de probabilité cumulative sont équivalentes à celles véhiculées par la fonction de probabilité correspondante. La version cumulative est parfois préférable pour les tableaux, parce que les problèmes d’arrondis sont plus graves lorsqu’on additionne plusieurs termes f(x) que lorsqu’on prend la différence de deux valeurs de F(x) pour obtenir une probabilité associée à une séquence consécutive de valeurs possibles, et parce qu’elle est plus facile à comprendre.